4.1.3. Метод ранговой корреляции

Алгоритм исследования имеет три этапа. Вначале определяют систему рангов, порядок их присвоения, формируют группу экспертов, которые распределяют ранги. Находя сумму рангов для факторов, их упорядочивают. На следующем этапе проверяют меру согласованности мнений экспертов с помощью коэффициентов ранговой корреляции. На последнем этапе устанавливается значимость именно коэффициентов ранговой корреляции.

а) Случай двух экспертов

Пример 4.1. Работники двух фирм оценили влияние 10 обобщенных факторов на хозяйственную деятельность фирм. Наибольшее значение ранга присваивалось самому существенному показателю. Необходимо провести статистический анализ результатов опроса.

Факторы	1	2	3	4	5	6	7	8	9	10
	6	4	10	3	2	8	9	1	7	5
	5	4	9	1	3	10	8	2	6	7

где – ранги представителей первой фирмы;– ранги представителей второй фирмы.

Решение.

1. Определим сумму рангов каждого фактора, а также среднее значение ранга

Таблица 4.1

Нахождение суммы рангов

Факторы	1	2	3	4	5	6	7	8	9	10
	11	8	19	4	5	18	17	3	13	12
	5,5	4,0	9,5	2	2,5	9,0	8,5	1,5	6,5	6,0

Расчеты свидетельствуют, что наиболее значимыми, по мнению опрашиваемых, следует назвать 3, 6, 7 и 9 факторы, а наименее существенными – 8, 4, 5 и 2 факторы.

2. Проверим согласованность мнений экспертов по критерию Спирмена.

а) Найдем коэффициент ранговой корреляции Спирмена по формуле (4.1.1):

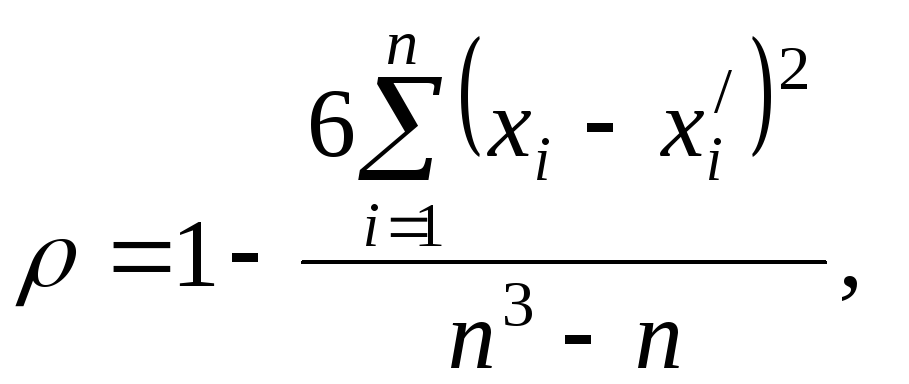(4.1.1)

В нашем случае , поэтому формула (26) имеет вид

Полученное значение свидетельствует о высокой степени согласованности мнений экспертов относительно влияния факторов (близко к 1).

б) Установим, будет ли значимым коэффициент Спирмена.

Критическую точку находим по формуле (4.2):

, (4.1.2)

где находим по таблице Стьюдента (приложение 5).

В нашем случае , найденное по формуле (4.1.2), равнопри.

Поскольку , то ранговую связь факторов следует признать значимой, коэффициенту ранговой корреляции и выводам о существенности факторов надо доверять.

3) Проверим согласованность экспертов по критерию Кендалла.

а) Найдем коэффициент ранговой корреляции Кендалла.

Для этого ранги первого эксперта разместим в возрастающей последовательности, ранги второго перенесем соответственно.

Таблица 4.2

Вспомогательные расчеты

	1	2	3	4	5	6	7	8	9	10
	2	3	1	4	7	5	6	10	8	9

Для каждого элемента второго ряда подсчитываем число рангов, которые его превосходят и расположены за ним. Подытоживая эти числа, получаем величину . В нашем случае она равняется

= 8+7+7+6+3+4+3+0+1 = 39.

Коэффициент ранговой корреляции Кендалла находим по формуле (4.1.3):

. (4.1.3)

В нашем случае формула (4.1.3) имеет вид .

Рассчитанный коэффициент подтверждает вывод, сделанный раньше: между экспертами существует высокая согласованность мнений о влиянии факторов.

б) Значимость коэффициента Кендалла проверяем, используя критическую точку, которую находят по формуле (4.1.4):

, (4.1.4)

где – критическое значение, которое найдем по таблице функции Лапласа из равенства:.

В нашем случае , тогда, поэтому, найденное по формуле (4.1.4), равняется.

Поскольку , то ранговая связь между факторами является существенной, коэффициент Кендалла заслуживает доверия, а выводы о влиянии факторов справедливы.