конспекты / 1234

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донбасская национальная академия строительства и архитектуры

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

AsA +BsB +CsC

.pdf

Скачиваний:

Добавлен:

21.02.2016

Размер:

1.55 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

Дві незбіжні точки утворюють симплекс прямої; три точки, які не належать прямій утворять симплекс площини; чотири точки, які не належать площині утворять симплекс простору. Симплекс складає геометричну частину визначника лінійної геометричної форми (прямої, площини або простору). Щоб заповнити симплекс безперервною безліччю точок і цим цілком визначити пряму, площину або простір, необхідно задати алгоритм утворення поточної точки М.

Поточну точку М площини АВС (рис. 5) B визначимо як вершину паралелограма NATM, де N,T

– поточні точки прямих АС, АВ:

P = (A - C)p + C; Q = (B - C)q + C.		Q	M
M = (A – C)p + C + (B - C)q + C – C =			M
M = (A – C)p + C + (B - C)q + C – C =
= Ap + Bq + C(1 – p - q).
Отже, рівняння площини визначається симплексом	C		А
АВС за допомогою двох незалежних параметрів p і q.	C		P
			Рис. 4.5

4.5. ТОЧКОВЕ РІВНЯННЯ ПЛОЩИНИ І ПРОСТОРУ В СТАНДАРТНІЙ ТА ПРИРОДНІЙ ПАРАМЕТРИЗАЦІЯХ.

	У симплексі АВС (рис. 4.6) поточну точку М						C
визначимо орієнтованими площами:

S = SABC;		SA = SMBC;		SB = SAMC;	SC = SABM.	MB
								MA
						SB	M
З точкового числення відомо, що рівняння площини								SA

через	площини		орієнтованих		трикутників
						SC
розташованих		проти		вершин	симплексного
трикутника виражається співвідношенням:						А

де sA +sB + sC = s.

Якщо в отриманому співвідношенні, площі замінити пропорційними величинами a, b, c, одержимо рівняння площини в стандартній параметризації:

	62
M =	Aa+Bb+Cc .
	a+b+c

Введемо позначення:

p = a+ab+c ; q = a+bb+c ; r = a+cb+c .

Тоді рівняння площини в природній параметризації матиме вигляд:

M = Ap + Bq +Cr,

де p +q +r =1.

Геометрична форма в площині визначається областю зміни параметрів відповідно до таблиці:

Значення параметрів p, q, r

p ≥ 0, q ≥ 0, r ≥ 0, p + q + r =1 p = 1, q = r = 0

q = 1, p = r = 0 r = 1, p = q = 0 p = 0, q + r = 1 q = 0, p + r = 1 r = 0, p + q = 1 p + q + r = 1

Таблиця

Геометрична форма

Трикутний відсік ABC площини

Точка А

Точка B

Точка C

Пряма BC

Пряма CA

Пряма AB

Площина α(А, B, C)

Параметрами визначається положення точки М щодо симплексу відповідно до схеми:

	Схема
	p > 0, q < 0, r > 0 .
p > 0, q < 0, r < 0.	p < 0, q < 0, r > 0.
A	B
	p > 0, q > 0,
	r > 0.
p > 0, q < 0, r < 0.	p< 0, q < 0, r > 0.
p > 0, q < 0, r < 0.	C

p < 0, q > 0, r < 0.

Геометрично природні параметри являють собою відношення орієнтованих відрізків

(рис. 4.6):

p = MMA ; q = MMB ; r = MMC . AMA BMB CMC

4.6. ОБЧИСЛЕННЯ ТОЧКИ ПЕРЕТИНУ ПРЯМОЇ ІЗ ПЛОЩИНОЮ

Обчислення точки перетину двох прямих і точки перетину прямої із площиною – найважливіші позиційні задачі курсу нарисної геометрії. Вони, як складові частини, входять у розв’язання багатьох задач. Перетин прямих у курсі розглядається або в площинах проекцій, або в площинах рівня. Отже прямі не можуть бути мимобіжними (точки, що визначають прямі, задаються двома координатами з трьох). Розглянемо цей випадок перетину прямих АВ і СD.

Через площі орієнтованих трикутників АСD	D
Через площі орієнтованих трикутників АСD
BCD визначаємо відношення АК/ВК.

Рис. 4.7

Введемо позначення:

x A

yA 1

yB 1

ACD =

BCD =

Тоді, із точкового числення, маємо:

(А - K)/(B - K) =	ACD/ BCD K = B ACD	−A BCD .		B
	ACD	− BCD	D	B
Аналогічно, визначимо точку K перетину прямої DE і			D	Рис.4.8
Аналогічно, визначимо точку K перетину прямої DE і
площини АВС (рис. 4.8):
DK/EK = DABC/	EABC, звідки маємо
	K = E DABC −D EABC .
	DABC −	EABC

Визначники четвертого порядку складені з координат точок мають вигляд:

	xE	yE	zE	1			xD	yD	zD 1
EABC =	xA	yA	zA	1	,	DABC =	xA	yA	zA	1	.
	xB	yB	zB 1				xB	yB	zB 1
	xC	yC	zC	1			xC	yC	zC	1

Обчислення визначників четвертого порядку

варто проводити способом перетворення або розкладання по координатах точок D і Е.

4.7. МЕТРИКА ТОЧКОВОГО ЧИСЛЕННЯ.

Для розв’язання метричних задач в точковому численні необхідно ввести метрику в точковій формі і на її основі визначити довжину відрізка, кут між прямими, площу трикутника, перпендикулярність прямих і таке інше.

4.7.1. МЕТРИЧНИЙ ОПЕРАТОР ТРЬОХ ТОЧОК. ДОВЖИНА ВІДРІЗКА ПРЯМОЇ. КУТ МІЖ ПРЯМИМИ.

У точковому численні особливе місце займає відношення відрізків прямої. Не менш важливу роль відіграє добуток цих відрізків. Спосіб координатного визначення добутку відрізків задає метрику простору, що характеризує властивості вимірів у цьому просторі.

Визначення: Метричним оператором точок АВС при точці А називається число, рівне добуткові довжин направлених відрізків АН і АВ, де Н - ортогональна проекція точки С на пряму АВ:

ΣABC = AH ×AB

Для Евклідового простору метричний оператор через Декартові координати заданих точок виражається співвідношенням:

ΣABC = Σ(B−A)(C−A)=

αBC

A B H

Рис. 4.9

=(x - x)(x - x) + (y - y)(y - y) + +(z – z)(z - z).

Звизначення метричного оператора випливає, що він не міняється при перестановці нижніх точок-індексів у позначенні:

ΣABC = ΣCBA .

Проекції Н відповідає безліч точок C на перпендикулярі до прямої АВ, отже, для

ΣCBA = AB2

кожної точки цієї безлічі метричний оператор не міняється. Нехай Н ≡ B, тоді

B частці випадку, коли C ≡ B, одержимо квадрат довжини відрізка.

ТВЕРДЖЕННЯ. Довжина відрізка АВ визначається співвідношенням:

AB = lAB = ΣABB .

Безпосередньо з рисунку (рис. 9), випливає:

		ΣA
ΣABC = AH ×AB = ΣCCA cosαBC × ΣABB	cosαBC =		BC	.
		ΣA
			ΣA
		BB	CC

							66
	4.7.2. ОСНОВА ПЕРПЕНДИКУЛЯРА, ОПУЩЕНОГО З ТОЧКИ НА ПРЯМУ.
Визначимо точку Н через метричні оператори (рис. 9). З геометричного змісту
метричних операторів випливає:
			ΣCAB = HB×AB,
			ΣABC = AH ×AB.
Розділивши другу рівність на першу, одержимо:
			AH =	ΣABC .
			HB	ΣCAB
Далі, застосовуючи точкове числення, одержимо:
	AH =	ΣABC	A−H =		ΣABC H =	AΣCAB +BΣABC .
	HB	ΣCAB	H−B		ΣCAB	ΣABC +ΣCAB
4.7.3. ТОЧКА ВИХОДУ З ПЛОЩИНИ ТА ЇЇ ГЕОМЕТРИЧНА ІНТЕРПРЕТАЦІЯ.
ТОЧКА ВИХОДУ З ПЛОЩИНИ НА ВІДСТАНЬ d.
Для побудов над площиною загального положення АВС уведемо поняття точки
виходу з площини на задану відстань d.
ВИЗНАЧЕННЯ. Точкою виходу з площини, заданої						K
ВИЗНАЧЕННЯ. Точкою виходу з площини, заданої
трикутником АВС, називається точка S(syz, szx, sxy) –						D	C
координатами якої є дійсні числа рівні подвоєним						D	C
координатами якої є дійсні числа рівні подвоєним						d
площам проекцій цього орієнтованого трикутника.						d
площам проекцій цього орієнтованого трикутника.
Точка S має наступні властивості:					d	S
1.	Довжина відрізка OS чисельно дорівнює					S
1.	Довжина відрізка OS чисельно дорівнює					A
площі трикутника АВС.						A
площі трикутника АВС.						s
2.	Пряма OS перпендикулярна			площині		s
2.	Пряма OS перпендикулярна			площині
трикутника АВС.						O	B
Такі ж властивості має векторний				добуток			B
Такі ж властивості має векторний				добуток			Рис. 4.10
двох векторів, утворених направленими відрізками
сторін орієнтованого трикутника АВС. Отже, точка виходу є точковим аналогом векторного
добутку векторів. Через координати вершин точка виходу з площини трикутника АВС
визначається співвідношеннями:

sABCYZ =

zA 1

sABCZX =

xA 1

sABCXY =

yA 1

;

Точка D розташована на прямій OS, для якої відрізок OD по довжині дорівнює числу d, одержала назву точки виходу з площини АВС на величину d:

D = Sd ,

sABC

де sABC – подвоєна площа трикутника АВС.

Точка D успішно використовується для побудов над площиною загального положення. Точка D (рис. 4.10), що піднімається над площиною від точки А на висоту d, визначається з паралелограма OAKD сумою точок:

K = A + D

4.7.4. ПЛОЩА ТРИКУТНИКА, РОЗТАШОВАНОГО В ПЛОЩИНІ ЗАГАЛЬНОГО ПОЛОЖЕННЯ.

Для визначення точки D необхідно мати подвійну площу трикутника АВС. Оскільки довжина відрізка OS, по визначенню, дорівнює цій подвійній площі, то через метричний оператор одержимо:

4s2ABC = ΣSOO = ΣS2 = (sABCyz )2 +(szxABC )2 +(sxyABC )2.

Здобувши корінь квадратний, знаходимо шукану подвійну площу.

4.7.5. ВИЗНАЧЕННЯ ВЕРШИНИ ПІРАМІДИ ПО ЗАДАНІЙ ОСНОВІ І ВИСОТІ.

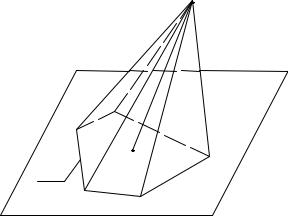
Розглянемо практичну задачу конструювання піраміди АВСК, по заданій основі АВС і висоті d, що проекціюється в центр ваги основи.

Конструювання піраміди зводиться до визначення вершини К.

1. Визначимо центр Т ваги трикутника АВС:

T = A+B+C . 3

ТРис. 4.11 В

2. Обчислюємо подвійні площі проекцій трикутника АВС:

sABCYZ =

zA 1

sABCZX =

xA 1

sABCXY =

yA 1

;

3. Визначаємо площу трикутника АВС, розташованого в площині загального положення:

s = (sxyABC )2 +(sABCyz )2 +(szxABC )2 .

4.	Знаходимо точку виходу з площини на висоту d:
	xD = sABCyz	d ; yD = sABCzx d
	s	s
5.	Обчислюємо координати шуканої вершини К:

= sxy d

; zD ABC .

xK = xD + xT ; yK = yD + yT ;zK = zD +zT .

Підводячи підсумок цієї лекції, відзначимо, що метричний оператор трьох точок споріднений скалярному добуткові векторів, точка виходу з площини – векторному добуткові двох векторів, а об’єм піраміди – змішаному добуткові трьох векторів.

Точкове числення, це математичний апарат інженера, що дозволяє конструювати геометричні об’єкти, а також лінійні і не лінійні форми. Розглянемо, як приклад, побудову піраміди.

4.8. ПОБУДОВА ВЕРШИНИ ТРИКУТНОЇ ПІРАМІДИ ПО ЗАДАНІЙ ОСНОВІ, ВИСОТА ЯКОЇ ПРОЕКЦІЮЄТЬСЯ В ЦЕНТРОИД ОСНОВИ.

Викладки цього розділу є розрахунковою основою одного із епюрів з курсу нарисної геометрії.

4.8.1. ВСТУП.

Будь-яка інженерна діяльність ґрунтується на математичному і геометричному моделюванні плоских і просторових форм. Опис цих форм спирається на одержання результату у виді зображення заданого геометричного образу. Проміжні етапи конструювання знаходять висвітлення у виді усе більш схематичних креслень, тому що процес створення більш конкретних і наочних зображень стає трудомістким і не встигає за мисленням конструктора. У складних інженерних конструкціях процес одержання зображення є гальмом у роботі конструктора.

Таким чином, потреби технічного розвитку вимагають значного прискорення етапів конструювання. Використання сучасних обчислювальних машин можуть забезпечити темпи створення не застарілих технологій і конкурентно здатної продукції. Виникає проблема гармонічного з'єднання образного мислення інженера з цифровою мовою ЕОМ. Цю задачу може успішно вирішити точкове числення, що з'єднує в собі геометричні образи з обчислювальними формулами. Точка в цьому численні є об'єктом обчислення і об'єктом геометричної формули. Конструктор, задаючи образ геометричними категоріями, може описувати етапи мислення обчислювальними формулами. Причому геометричний алгоритм конструювання формули знаходить висвітлення в обчислювальному алгоритмі, що переводиться програмістом на мову ЕОМ без посередника – математика. Якщо ж конструктор володіє знаннями програміста, то він у своє розпорядження одержує ЕОМ, як універсальний інструмент швидкого, точного зображення на екрані дисплея процесу конструювання.

4.8.2. БАЗОВІ ПОНЯТТЯ 1. Базові поняття розв’язання інженерно-графічної задачі: побудова піраміди по

заданій основі і висоті d на основі порівняння двох алгоритмів геометричного й обчислювального.

Для побудови креслення, як відомо, необхідно мати об'єкт (оригінал), картинну площину (площина проекцій) і алгоритм (правило) побудови креслення.

Під об'єктом (оригіналом) домовимося розуміти будь-який реальний або уявний технічний пристрій або окрему деталь. При цьому в процесі побудови креслення нас цікавлять тільки його геометричні особливості, тобто характер і ступінь складності обмежуючих його поверхонь, а також окремі точки і лінії. Сукупність цих особливостей оригіналу умовимося називати його геометричним образом.

Геометричний образ оригіналу може бути досить складним. Тому для зручності вивчення розіб'ємо його на більш прості геометричні образи – точки, лінії, поверхні.

Найбільш простим геометричним образом є точка. Геометричні елементи більш високого рівня складності можуть бути утворені кінематичним способом, тобто шляхом переміщення в просторі більш простих геометричних елементів по визначеному закону. Так,

	наприклад, лінія може бути утворена рухом точки,	S
	поверхня – рухом лінії.	S
	поверхня – рухом лінії.
	Для побудови креслення необхідно задати
	послідовність виконання дій для досягнення
	поставленої в умові мети, тобто алгоритм

	розв’язання задачі.	П1
	Як алгоритм побудови креслення прийнята
	паралельна проекція, в основі якої лежить метод	O
	проектування.	O
	Для побудови креслення оригінал необхідно	m
	Для побудови креслення оригінал необхідно
	попередньо задати, тобто описати таким чином,
	щоб побудувати будь-яку його точку, а також	Рис. 4.12
	зафіксувати його в просторі. За умовою задачі нам	Рис. 4.12
	зафіксувати його в просторі. За умовою задачі нам

необхідно задати відсутню вершину трикутної піраміди по заданій основі і висоті d, при цьому висота проекціюється в центроїд основи піраміди.

Ми не будемо зупинятися докладно на способах завдання пірамідальних поверхонь. Зупинимося на способі побудови піраміди.

Якщо пірамідальну поверхню перетнути площиною П1, то тіло, обмежене пірамідальною поверхнею і цією площиною прийнято називати пірамідою (рис.4.12). Частина площини П1, обмежена багатокутником m, називається основою піраміди, а пірамідальна поверхня – бічною поверхнею. Перпендикуляр SO, опущений з вершини S на основу, називають висотою піраміди.

У такий спосіб піраміда – це геометричне тіло, у якого основа – довільний багатокутник, а бічні грані – трикутники з загальною вершиною S, названою вершиною піраміди. Перпендикуляр, опущений з вершини на підставу, називається висотою піраміди. Назва піраміди залежить від кількості бічних граней (тригранна, якщо в неї три бічні грані і т.д.).

Поняття центроїда основи піраміди, як взагалі будь-якої плоскої фігури, довільно заданої в просторі тісно зв'язано з ім'ям німецького вченого А.Ф. Мьобіуса, що у 1827р. у своїй роботі “Барицентричне числення” започаткував основи прямим операціям над геометричними об'єктами.

Числення починається з того, що визначаються об'єкти і дії над ними. Об'єктами алгебраїчних операцій у Мьобіуса служили точки (точкове числення), до яких він приєднував маси, узагальнивши поняття маси в тому напрямку, що вона може приймати не тільки додатні, але і від’ємні значення.

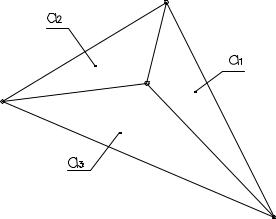
При розв’язанні задач про те, які маси Т1, Т2, Т3 варто помістити в точках A, B, C, щоб вони визначили єдиний центроїд Т площини ABC, як показано на рис. 4.13 А. Мьобіус ввів поняття барицентричних координат, для яких значення має тільки їх відношення. З'єднуючи

точку Т с точками A, B, C

Мьобіус прийшов до висновку про те, що площі отриманих

трикутників TBC (a1); TAB (a3); TCA (a2)

C T3

пропорційні

барицентричним

координатам точки Т, наприклад:

;

T 3

a 3

T 2

a 2

і їхнє відношення з умови визначення

центроїда трикутника дорівнює 1, тобто

= 1

T =T =T

; T 2

;

T 3

Випадок,

коли

точка

Рис. 4.13

знаходиться

поза

трикутником

B T2

враховується

за

допомогою

угоди

орієнтованістю трикутника.

Такі нормовані барицентричні координати були названі ареальними, тому що вони в точності рівні площам трикутників, якщо прийняти площу всього трикутника за одиницю виміру, тобто

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

Соседние файлы в папке конспекты

#
21.02.20161.83 Mб20------_-----.pdf
#
21.02.2016441.9 Кб17---.---.1-- -.--.pdf
#
21.02.2016706.64 Кб23---_-------_Excel (1).pdf
#
21.02.2016706.64 Кб20---_-------_Excel.pdf
#
21.02.20164.64 Mб43123.pdf
#
21.02.20161.55 Mб201234.pdf
#
21.02.2016855.41 Кб32end_3.pdf