
Стрмех_3_У_2002
.pdfМІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ ДОНБАСЬКА НАЦІОНАЛЬНА АКАДЕМІЯ БУДІВНИЦТВА І АРХІТЕКТУРИ
КАФЕДРА ТЕОРЕТИЧНОЇ І ПРИКЛАДНОЇ МЕХАНІКИ
Мущанов В.П., Жук М.Р., Гіжко В.Т.
КОНСПЕКТ ЛЕКЦІЙ з дисципліни
«БУДІВЕЛЬНА МЕХАНІКА»
(для студентів будівельних спільностей)
Частина 3
Затверджено на засіданні кафедри теоретичної та прикладної механіки Протокол № 1 от 29.01.2010 Завідувач кафедри проф. Мущанов В.П.
Макіївка, 2010
Конспект лекцій. Будівельна механіка. Частина 3. В.П. Мущанов, М.Р. Жук, В.Т. Гіжко. – 68 с.
Конспект лекцій призначено для студентів будівельних спеціальностей вузів. Містить у собі три розділи спеціального курсу будівельної механіки. Метод кінцевих елементів, стосовно до розрахунку плоских стержневих систем, стійкість споруд і основи динаміки споруд. Теоретичний матеріал ілюструється малюнками, приводяться приклади рішення задач.
Рецензент доц. Демидов О.І.
|
ЗМІСТ |
Розділ 1. Метод кінцевих елементів |
.............................................................................4 |
Лекція 1.............................................................................................................................. |
4 |
Лекція 2.............................................................................................................................. |
6 |
Лекція 3............................................................................................................................ |
10 |
Лекція 4............................................................................................................................ |
13 |
Додаток............................................................................................................................ |
18 |
Розділ 2. Стійкість споруд............................................................................................ |
21 |
Лекція 5............................................................................................................................ |
21 |
Лекція 6............................................................................................................................ |
23 |
Лекція7............................................................................................................................. |
28 |
Лекція 8............................................................................................................................ |
34 |
Лекція 9............................................................................................................................ |
40 |
Лекція 10.......................................................................................................................... |
44 |
Лекція 11.......................................................................................................................... |
46 |
Розділ 3. Основи динаміки споруд ............................................................................. |
50 |
Лекція 12.......................................................................................................................... |
50 |
Лекція 13.......................................................................................................................... |
52 |
Лекція 14.......................................................................................................................... |
54 |
Лекція 15.......................................................................................................................... |
55 |
Лекція 16.......................................................................................................................... |
59 |
Лекція 17.......................................................................................................................... |
61 |
Лекція 18.......................................................................................................................... |
66 |
Розділ 1. Метод кінцевих елементів
Лекція 1
Наближені методи розрахунку в будівельній механіці
Більшість задач будівельної механіки, зв'язаних з дослідженням пружньодеформованого стану конструкцій та їх елементів (стержнів, пластин, оболонок) зводиться, як правило, до рішення одного чи декількох диференціальних рівнянь рівноваги елемента, відповідно з одним чи декількома невідомими.
Точне рішення таких рівнянь (рішення в замкнутому вигляді) не представляє утруднень лише в деяких елементарних випадках. При рішенні реальних задач часто приходиться зіштовхуватися з таким обсягом обчислювальних робіт, що від точного рішення відмовляються, а в багатьох випадках точне рішення задачі взагалі неможливо, тому що граничні умови на контурі просто не виражаються в аналітичній формі. Тому, як правило, при рішенні практичних задач приходиться прибігати до наближених методів рішення.
Наближені методи рішення задач можуть бути розбиті на дві основні групи:
1.Варіаційні методи, що дають наближені аналітичні вираження шуканої функції (функції переміщень, функції внутрішніх зусиль).
2.Чисельні методи, що дають значення шуканої функції при тих чи інших значеннях аргументу.
До першої групи відносяться варіаційні методи Рітца, Бубнова-Гальоркіна, метод Треффца та інші.
До другої групи відносяться метод сіток і його більш розроблена модифікація - метод кінцевих елементів, а також ряд графічних і напівграфічних методів таких, як, наприклад, метод прямих, метод коллокацій та інші.
Перевага варіаційних методів полягає в тому, що задача зводиться, звичайно, до рішення системи двох, трьох, рідко чотирьох рівнянь, що дають гарне наближення до дійсного стану споруди. До їх недоліків варто віднести те, що можливості варіаційних методів обмежені складними контурами і складними законами розподілу зовнішнього навантаження, тому що застосування варіаційних методів вимагає, щоб було, хоча б у наближеній формі, визначене аналітичне вираження зовнішнього навантаження, деформованої пружної поверхні елемента та інших умов задачі.
Чисельні методи, у порівнянні з варіаційними, мають більш універсальний характер, тому що не вимагають аналітичних виражень умов задачі. Однак чисельні методи мають ряд недоліків. Так, для одержання задовільного рішення вони вимагають нанесення на досліджувану область густої сітки або розбивки на досить велике число елементів, що неминуче веде до рішення систем алгебраїчних рівнянь з великим числом невідомих, що стає можливим тільки при наявності ЕОМ. Крім того, чисельні методи часто приводять до неточності рішень, особливо в місцях дії зосереджених сил, при наявності гострих кутів, підкріплень і т.п., тобто там, де порушується гладкість полів перемінних.
Дуже істотним недоліком чисельних методів є те, що вони не дають аналітичного вираження шуканої функції, а, отже, для визначення параметрів пружно-деформованого стану в даній області приходиться обчислювати ці величини у всіх вузлах стикування елементів, тобто одержувати масу непотрібної інформації для тих областей, що нас зовсім не цікавлять.
Таким чином, вибір методу розрахунку при розгляді конкретної пружної системи залежить від постанови задачі і вихідних умов, а також від озброєності розраховувача обчислювальною технікою.
Метод кінцевих елементів (МКЕ)
Історично виникнення МКЕ пов'язане з ідеєю застосування добре розроблених процедур для розрахунку статично невизначених стержневих систем до рішення континуальних задач.
Спочатку ця ідея була висловлена ще в 1933 році І.М. Рабіновичем, але розвиток отримала тільки в 70-х роках ХХ-сторіччя, з появою ЕОМ.
Метод кінцевих елементів заснований на умовному представленні суцільного тіла у вигляді сукупності окремих кінцевих елементів, взаємодіючих між собою в кінцевому числі точок, що у МКЕ прийнято називати вузлами.
Система розбивається на прості кінцеві елементи (КЕ) пружно-деформований стан яких досліджується заздалегідь.
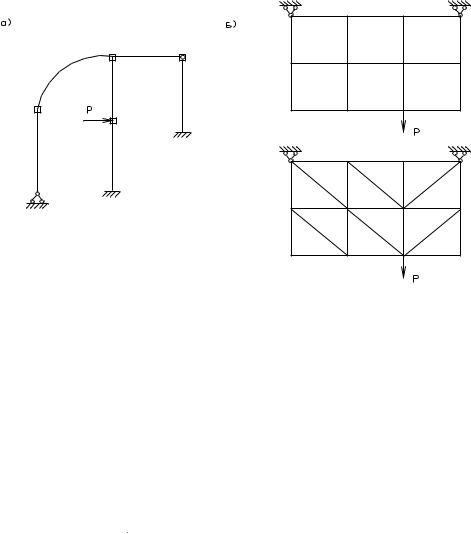
Так, наприклад, стержневі системи можуть бути розбиті на елементи у вигляді прямолінійних чи криволінійних стержнів (наприклад, для розрахунку арок) з різними умовами з'єднання елементів у вузлах. У цьому випадку дискретна модель є точною копією вихідної конструкції (з обліком прийнятих технічних гіпотез).
У розрахунках пластин найбільше поширення одержали прямокутні і трикутні кінцеві елементи. Тут дискретна модель лише приблизно відбиває поводження вихідної конструкції.
Помітимо, що навіть при тому самому числі вузлових точок різні схеми дискретизації вихідної конструкції породжують різницю в остаточних результатах розрахунку. На жаль, заздалегідь сказати, яка з можливих схем дискретизації приведе до найменшої погрішності розрахунку, неможливо.
Число ступенів свободи КЕ, а в остаточному підсумку число невідомих МКЕ, визначається кількістю накладених у вузлах додаткових зв'язків.
Умови рівноваги і спільності деформацій виконуються тільки у вузлових точках, точках з'єднання КЕ. Однак це не виходить, що загальна жорсткість пластини при цьому різко зменшується, оскільки залежність між вузловими зусиллями і деформаціями кожного елемента розглядається з обліком деяких внутрішніх зв'язків.
Кожен елемент є частиною замінюємого середовища, тобто суцільне тіло лише умовно поділяється на окремі елементи кінцевих розмірів. Виділений елемент має ті ж фізичні властивості і геометричні характеристики, що і розглядаєма конструкція в місці розташування елемента.
Усі зовнішні сили вважаються прикладеними у вузлах, по напрямку їх можливих переміщень. Поза вузлові навантаження попередньо приводяться до вузлового.
При реалізації МКЕ найбільше поширення одержали ідеї методу переміщень, хоча маються роботи, де розглядається метод сил і змішаний метод. Перевагу методу переміщень віддано в основному через простоту вибору основної системи, складання матриці жорсткості і формування вектора зовнішніх навантажень.
Вирішувальне рівняння МКЕ являє собою матричну форму канонічних рівнянь методу переміщень. і, має вигляд:
[r]{Z}={P},
де: [r] - матриця жосткості споруди в цілому,
{Z}- вектор переміщень вузлових точок споруди, {P}- вектор зовнішніх навантажень.
Підхід до рішення задачі МКЕ є єдиним, як для стержневих систем, так і для пластин, оболонок та масивів.
Подальший розгляд МКЕ будемо проводити на прикладі плоских стержневих систем.
Лекція 2
Метод кінцевих елементів у розрахунках плоских стержневих систем
Розгляд пружних систем взагалі і плоских стержневих систем зокрема з позицій МКЕ є представленням пружних систем у виді набору елементів з кінцевим числом ступенів свободи, які з'єднуються між собою у вузлових точках (вузлах). Таке представлення заданої системи у вигляді дискретної моделі приводить до повної формалізації всіх етапів розрахунку. Підхід до рішення задачі є єдиним, як для стержневих систем, так і для пластин, оболонок, об'ємних тіл і т.п.
Розглядати будемо МКЕ розроблений на базі методу переміщень, стосовно до розрахунку плоских стержневих систем.
При розрахунку плоских стержневих систем у МКЕ прийняті ті ж гіпотези, що й у звичайному методі переміщень. Трохи уточнюється тільки одна гіпотеза: у МКЕ будемо враховувати вплив не тільки згинальних, але і вплив поздовжніх деформацій на переміщення вузлових точок споруди. Тобто довжина стержня в результаті деформацій розтягання або стиску може змінюватися. Це положення дозволяє більш формалізувати вибір основної системи МКЕ й одержати результати розрахунку більш точні, ніж у звичайному методі переміщень.
Розрахунок стержневих систем, як і будь-яких інших, у МКЕ починають з розбивки заданої системи на окремі кінцеві елементи.
В якості кінцевих елементів (КЕ) ми будемо розглядати прямолінійні стержні, що мають постійну жорсткість по довжині. Між собою КЕ можуть з'єднуватися або жорстко, або за допомогою шарніра. Точки з'єднання елементів у МКЕ називають вузловими, чи вузлами.
Тобто основну систему (дискретну модель) МКЕ одержують, розбиваючи задану систему на окремі прямолінійні елементи, що мають постійну жорсткість по довжині. При наявності в системі криволінійних чи стержнів з перемінною жорстікстю, їх, з достатнім ступенем точності, розбивають на ділянки, у межах яких стержні вважають прямолінійними, з усередненою постійною жосткістю.
Крім того, алгоритм МКЕ вимагає, щоб усі зовнішні навантаження, що діють на споруди, були прикладені до вузлових точок її дискретної моделі. Тому, точки де діють зосереджені сили роблять вузловими, а навантаження, розподілені по довжині стержня, перетворюють до вузлового.
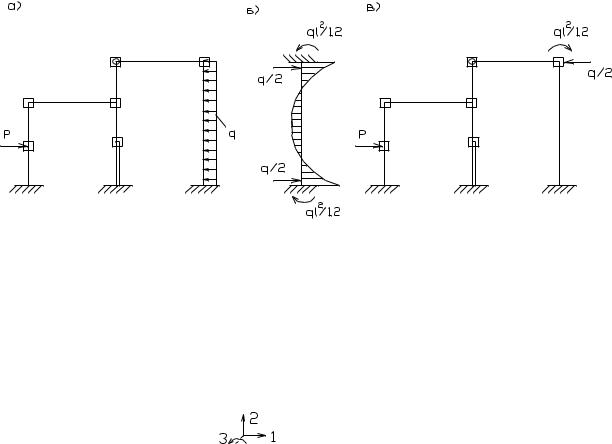
Для перетворення поза вузлових навантажень до вузлового, використовують таблиці методу переміщень (див. рис. б).
У вузлах, де окремі елементи з'єднуються між собою жорстко, мається три невідомих переміщення, у шарнірних вузлах – два. Отже, кількість невідомих МКЕ можна визначити:
n = 3nж.вуз. + 2nш.вуз .
Позитивні напрямки і порядок нумерації невідомих приймаємо наступним чином
Дискретна модель споруди в цілому, що зв'язується з загальною системою осей координат, характеризується n параметрами переміщень Zi і вузлових силових впливів Pi , що складають вектори
Z1
|
|
|
Z2 |
||
{Z} |
|
|
|
|
|
|
|
|
|
|
|
Zn |
|
|
P1
P |
|
|
|
2 |
|
{P} |
|
|
|
|
|
|
|
|
P |
|
|
|
n |
|
Кожний кінцевий елемент зв'язаний з місцевою системою осей координат і характеризується своїми параметрами вузлових переміщень {V} і відповідними вузловими зусиллями {S}’. Крім того, для елементів, у межах яких поза вузлове навантаження перетвориться до вузлового, формують вектори вантажних зусиль {So}.
В рівнянні МКЕ
[r]{Z}={P},
матриця [r], що зветься матрицею жорсткості споруди в цілому, формується з матриць жорсткості окремих елементів.
Матриця жорсткості КЕ в місцевій системі осей координат
Матриця жорсткості КЕ в місцевій системі осей координат [r]j’ установлює зв'язок між одиничними переміщеннями і зусиллями у вузлових точках, для горизонтально розташованого елемента.
Як уже відзначалося, основна система МКЕ являє собою сукупність окремих стержнів, що з'єднуються між собою жорстко чи за допомогою шарнірів. Отже, усе різноманіття КЕ можна звести до трьох типів елементів:

а) елемент із двох сторін обмежений жорсткими вузлами, такий елемент має шість ступенів свободи, тобто невідомими є шість можливих переміщень вузлових точок елемента
б) елемент з однієї сторони обмежений жорстким вузлом, а з іншої шарнірним, такий елемент має п'ять ступенів свободи
г) елемент із двох сторін обмежений шарнірними вузлами, такий елемент має чотири ступені свободи
Розглянемо формування матриць жорсткості для показаних вище трьох типів КЕ, у місцевій системі осей координат.
Для елемента із шістьма ступенями свободи (тип а) матриця жорсткості буде мати вигляд:
|
r11' |
r21' |
r16' |
|
|
[r]j’= |
r' |
r' |
|
r' |
|
21 |
22 |
. |
26 |
, |
|
|
. |
. |
. |
|
|
'r62' . r66'r61
де r12’ - реактивне зусилля в зв'язку 1 від одиничного переміщення зв'язку 2 і т.д. У блоковому виді матриця [r]jэ буде мати вигляд
r' |
r' |
|
[r]j’= нн' |
нк' |
, rнн |
rкн |
rкк |
|
де rнк’ - блок реакцій у зв'язках, накладених на початковий вузол, від одиничних переміщень зв'язків, накладених на кінцевий вузол КЕ і т.д.
Чисельні значення реакцій будемо визначати, використовуючи таблиці методу переміщень. Знак реакцій буде додатнім, якщо напрямок реакцій збігається з позитивним напрямком переміщень Vj.
1.Формування матриці жорсткості для елемента із шістьма ступенями свободи (тип а)
2 |
5 |
1 |
4 |
3 |
6 |
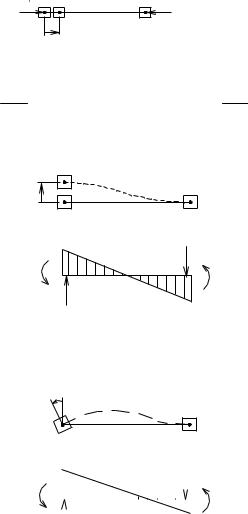
Задамо послідовно одиничні переміщення зв'язкам V1=1, V2=1...V6=1. 1) V1=1
|
EF |
|
EF |
|
l |
|
l |
|
|
V1 =1 |
|
У відповідністі із законом Гука |
|
||
l = |
Nl , |
l = V1 = 1, |
N = EF , |
|
EF |
|
l |
2) V2=1
V2 =1
|
12EJ |
|
l3 |
6EJ |
6EJ |
l2 |
|
l2 |
12EJ |
|
l3 |
3) V3=1
V3 =1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6EJ |
|
|
|
|
2EJ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
4EJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
l2 |
|
|
|
6EJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
і т.д. задаємо |
V4 = 1, |
|
|
|
|
V5 = 1, |
|
V6 = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Розставляючи реакції у відповідні осередки, одержимо матрицю жорсткості для |
|||||||||||||||||||||||||||||||||||||||||||||||||||
елемента із шістьма ступенями свободи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
EF |
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
EF |
|
|
0 |
|
|
|
|
|
0 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
l |
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
12EJ |
|
|
|
6EJ |
|
|
|
|
0 |
|
|
|
|
12EJ |
|
6EJ |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
l3 |
|
|
|
|
l2 |
|
|
|
|
|
|
l3 |
|
|
l2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
’ |
|
0 |
|
|
|
|
|
6EJ |
|
|
|
|
4EJ |
|
|
|
|
|
0 |
|
|
|
|
6EJ |
|
|
2EJ |
|
|
|||||||||||||||||||||
|
= |
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
l |
|
|
|
|
|
|
|
l |
|
|
|
|
|
l |
|
|||||||||||||||||||||
|
[r]j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
EF |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EF |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|||||||||||||||
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
12EJ |
|
|
|
|
6EJ |
|
|
|
|
|
12EJ |
|
|
6EJ |
|
|||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
l3 |
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
|
l3 |
|
|
|
l2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
0 |
|
|
|
|
|
6EJ |
|
|
|
2EJ |
|
|
|
|
0 |
|
|
|
|
6EJ |
|
4EJ |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
l |
2 |
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
l |
2 |
|
|
|
|
l |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Запишемо матриці жорсткості для двох інших типів елементів, формуючи їх аналогічно попередній.
2. Матриця жорсткості для елемента з п'ятьма ступенями свободи (тип б) буде
мати вигляд
|
EF |
|
|
0 |
|
|
|
0 |
|
|
EF |
|
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
l |
|
|
|
|
|
l |
|
|
|||||||||||
|
0 |
|
|
3EJ |
|
3EJ |
|
|
0 |
|
|
3EJ |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
l3 |
|
|
l2 |
|
|
l3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
[r]j’ = |
0 |
|
|
3EJ |
|
|
3EJ |
|
|
|
0 |
|
|
3EJ |
|
|||||
|
|
|
l2 |
|
|
l |
|
|
l2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
EF |
|
|
|
|
|
|
|
|
|
EF |
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
0 |
|
|
|
|
0 |
|
|
||||||
l |
|
|
|
|
|
|
|
|
l |
|
|
|||||||||
|
|
|
|
3EJ |
|
|
3EJ |
|
|
|
3EJ |
|
|
|||||||
|
0 |
|
|
|
|
|
0 |
|
|
|
||||||||||
|
l3 |
l2 |
|
|
|
|
|
l3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3. Матриця жорсткості для елемента з чотирма ступенями свободи (тип в)
запишеться
|
|
EF |
|
|
|
EF |
|
|||
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
l |
l |
|||||||
’ |
|
|
0 |
|
|
|
||||
= |
|
0 |
|
|
|
0 |
|
0 |
||
[r]j |
|
EF |
|
|
EF |
|
||||
|
|
|
|
0 |
|
|
|
|
0 |
|
|
l |
|
|
l |
||||||
|
|
|
0 |
|
|
|
||||
|
|
|
0 |
|
|
|
0 |
|
0 |
|
Лекція 3
Матриця перетворень (направляючих косинусів)
Розглянемо тепер кінцевий елемент в складі рами, розташований під кутом до осі Х в загальній системі осей координат.
Необхідно перейти від матриці реакцій [r]’j у місцевій системі осей координат до матриці [r] у загальній системі координат.
Задачу вирішуємо таким чином. На початку побудуємо матрицю [c]j, що перетворить переміщення КЕ {z}j у загальній системі осей координат у переміщення {v}j, за формулою
{v}j = [c]j {z}j
