Стрмех_2_У_1999

2

Конспект лекцій з дисципліни «Будівельна механіка» Частина 2 (для студентів будівельних спеціальностей) / В.П. Мущанов, М.Р. Жук, В.Т.Гіжко. – 55 с.

Конспект лекцій призначено для студентів будівельних спеціальностей вузів. В конспекті подано матеріал про статично невизначні системи, статично невизначні ферми, нерозрізні балки, статично невизначні комбіновані системи, статично невизначні арки, розглядається метод переміщень, метод сил, а також змішаний метод розрахунку рам та комбінований розрахунок симетричних рам.

Теоретичний матеріал ілюструється рисунками, наводяться приклади вирішення завдань.

Рецензент доц. Демідов О.І.

3

ЗМІСТ

Лекція №22. Спрощення канонічних рівнянь методу сил при розрахунку симетричних

4

Лекція №19. Статично невизначні стержневі системи

Статично невизначної називається така система, яка не може бути розрахована за допомогою одних тільки рівнянь статики, так як вона має “зайві" зв'язки. Іншими словами, якщо в даній системі число невідомих опорних реакцій і зусиль M, Q, N в елементах системи перевищує число рівнянь рівноваги, то така система статично невизначна. Для розрахунку таких систем складають додаткові рівняння, які в тому або іншому вигляді враховують деформації системи.

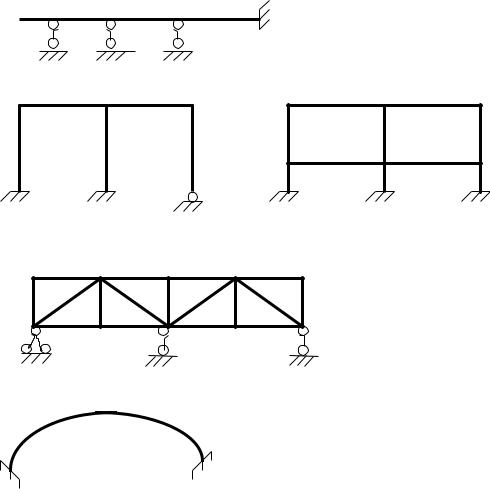
У процесі вивчення курсу будемо розглядати 4 основних вигляду статично невизначних систем:

а) статично невизначні балки

= 3

б) статично невизначні рами

в) статично невизначні ферми

г) статично невизначні арки

= 3

Основні властивості статично невизначних систем:

1)статично невизначні системи більш економічні, ніж статично визначні, так як виникаючі в них зусилля при тих же навантаженнях звичайно менше зусиль статично визначних систем;

2)зусилля, виникаючі в елементах статично невизначних систем залежать від жорсткості елементів: чим більше жорсткість елемента, тим більше виникаючі в йому зусилля;

3)статично невизначні системи більш надійні в роботі, так як при виході з ладу якого-небудь елемента, зусилля перерозподіляються на інші елементи системи;

4)в статично невизначних системах, на відміну від статично визначних внутрішні зусилля можуть виникати навіть при відсутності навантажень: від осідання опор, зміни температури і т.д.

5

Методи розрахунку статично невизначних систем.

Існує декілька методів розрахунку статично невизначних систем, але всі вони являють собою видозміни двох основних методів: методу сил і методу переміщень.

I.Метод сил. Названий так тому, що в додаткові рівняння цього методу як невідомі входять опорні реакції і внутрішні зусилля M, Q, N в яких-небудь перетинах.

II. Метод переміщень. Як невідомі цього методу приймаються кутові і лінійні переміщення вузлових точок споруд.

III. Змішаний метод. У додаткові рівняння цього методу як невідомі входять як зусилля, так і переміщення вузлових точок споруди.

IV.Комбіноване рішення. Застосовується при розрахунку симетричних рам: на прямосиметрічні навантаження раму розраховують методом переміщень, на кососиметрічні навантаження - методом сил.

Метод сил.

Міра статичної невизначенності систем.

Розрахунок статично невизначних систем починають з аналізу розрахункової схеми споруди. Це необхідне для того, щоб визначити міру статичної невизначенності системи, яка рівна числу зайвих зв'язків:

тут: Сопчисло опорних зв'язків; Шо - число простих шарнірів; D - число жорстких дисків.

Наприклад:

= 5 + 1 - 3*2 =1

Однак, ця формула справедлива лише в тому випадку, якщо окремі диски не є замкненими контурами, тобто кожний з них сам по собі статично визначимо. Якщо ж рама має замкнені контури, то необхідно враховувати ще і статичну невизначенність кожного такого контура.

Р

М

N N

Q Q

Замкнений контур тричі статично невизначний

6

M = 0; тобто = 2,

тобто простий шарнір зменшує міру статичної невизначенності замкненого контура на 1 одиницю.

Таким чином, для рам, що мають замкнені контури, міра статичної невизначенності визначається по формулі:

зв'язків. Замість відкинутих зв'язків прикладають невідомі узагальнені сили X1, X2,. ......., Xn.

“Зайві" зв'язки потрібно видаляти таким чином, щоб отримана основна система у всіх своїх частинах була статично визначною і геометрично незмінної.

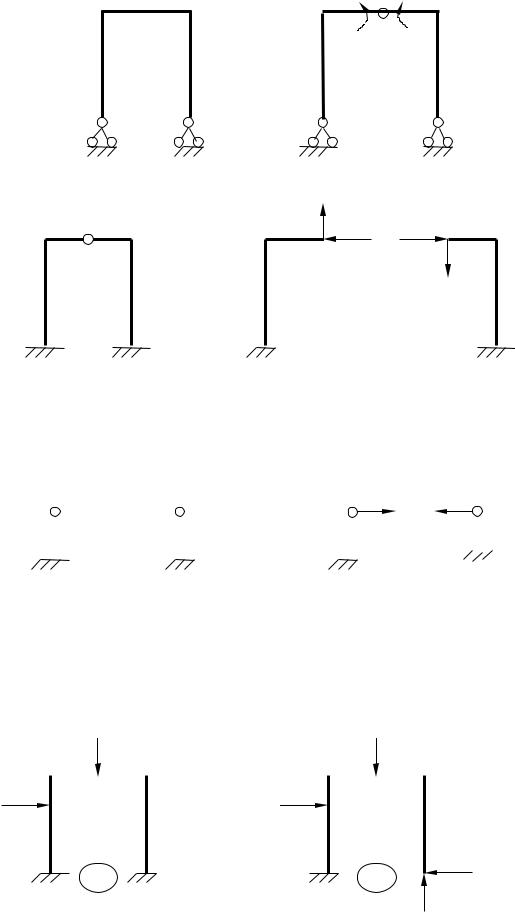
Способи утворення основних систем:

1) можна відкинути “зайві" опорні зв'язки, і у напрямі відкинутих зв'язків прикласти невідомі опорні реакції;

2) можна розрізати суцільний брус і в перетині прикласти парні моменти, поперечні і подовжні сили;

X3 X2

= 3

7

3) можна видалити один внутрішній зв'язок, вводячи на вісь жорсткого елемента шарнір;

Х1

= 1

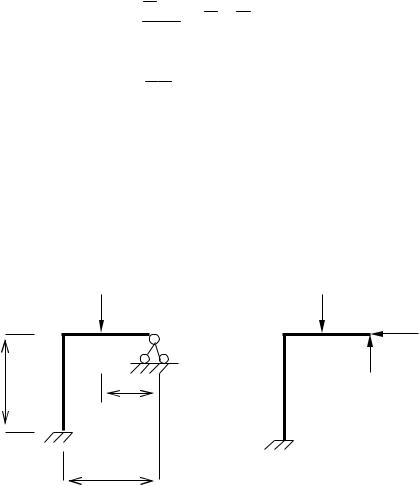
4) можна зробити розріз по шарніру, це рівносильно видаленню двох внутрішніх зв'язків: поперечної і подовжньої сил;

X1

X2 X2

X1

= 2

5)можна розрізати стержень, з двох сторін прикріплений шарнірно до системи. У такому незавантаженому стержні виникає одна подовжня сила.

Канонічні рівняння методу сил.

Ідея методу сил: в заданій системі переміщення у напрямі відкинутих зв'язків рівні нулю. У основній системі у напрямі відкинутих зв'язків переміщення можуть бути як = 0, так і ( 0. Щоб задана і основна системи були рівноцінні в значенні зусиль і деформацій, необхідно підібрати такі зусилля X1, Х2,. . , Хn щоб переміщення у напрямі відкинутих зв'язків, в основній системі, від дії зовнішнього навантаження і зусиль X1, Х2,. . , Хn також дорівнювали нулю.

X2

8

тобто

i = iP + iX1 + iX2 +.......+ iXn = 0 ,

де

iXn = in Xn ,

тоді

i = ii Xi + i2 X2 + ....... + in Xn + iP = 0;

де i1 - переміщення у напрямі і від дії X1 = 1.

iP - переміщення у напрямі і від дії зовнішнього навантаження.

Якщо система має n невідомих, то система канонічних рівнянь методу сил запишеться:

1е рівняння: переміщення у напрямі X1 від дії невідомих X1, X2,. .. , Xn і зовнішнього навантаження, в основній системі, повинно дорівнювати нулю.

Коефіцієнти з однаковими індексами іі - називають головними коефіцієнтами, ік - побічними, причому ік = ік (на основі теореми Максвелла), ір - вантажний коефіцієнт.

Лекція №20. Визначення коефіцієнтів системи канонічних рівнянь

ii - переміщення у напрямі Xі від дії Xі = 1

2

ii = MEIi dx Mi MI ,

тобто для знаходження коефіцієнта ii треба побудувати епюру згинаючих моментів від дії сили Xі = 1 і перемножити її за правилом Верещагина саму на себе.

тобто, будуємо епюри згинаючих моментів від дії Xі = 1 та від зовнішнього навантаження і перемножуємо їх за правилом Верещагіна.

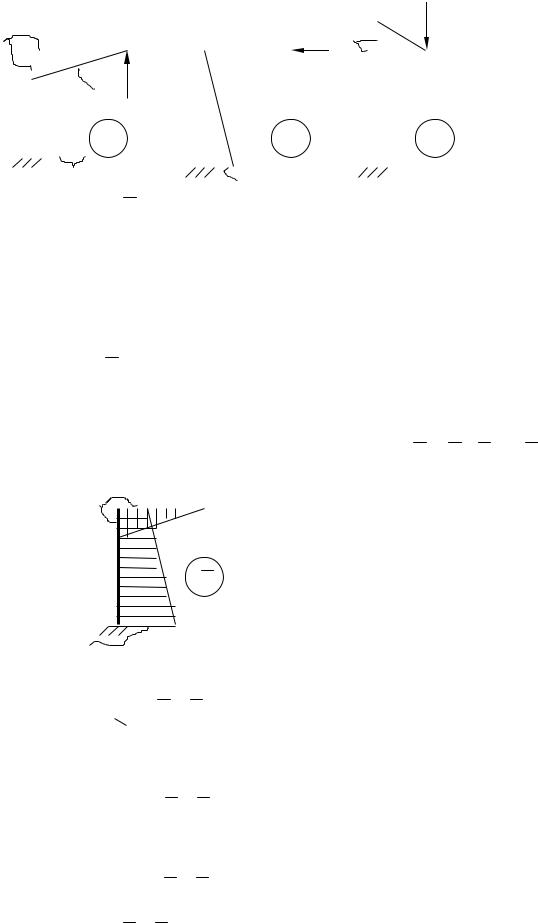
Приклад:

О.С.

iiX1 12X2 1p 0;

21X1 22X2 2p 0;

l

9

Перевірка правильності обчислення коефіцієнтів.

Для виконання перевірок будується сумарна одинична епюра MS M1 M2 ... Mn , отримана шляхом складання усіх одиничних епюр, в прикладі:

l

MS

l+h

1. Універсальна перевірка одиничних коефіцієнтів полягає в тому, що сума всіх одиничних коефіцієнтів дорівнює результату множення сумарної одиничної епюри самої на себе:

ii 2 ik MS MS

в прикладі:

11 22 2 12 MS MS

2. Порядова перевірка одиничних коефіцієнтів полягає в тому, що сума одиничних коефіцієнтів одного рівняння і дорівнює результату перемноження сумарної одиничної епюри на Mi:

i1 i2 ... in MS MS

в прикладі:

11 12 MS M1