Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4613 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Донбасская национальная академия строительства и архитектуры
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Стрмех_3_У_2002

.pdf
Скачиваний:
26
Добавлен:
21.02.2016
Размер:
834.02 Кб
Скачать
☆

Якщо цю масу умовно вважати точковою, то її положення на площіні буде характеризуватися двома параметрами W = 2, а в просторі – трьома W = 3.

У

m

y

Х

x

Усяка розподілена маса на пружньо-деформуємій системі, яку можна розглядати як нескінченно велику кількість нескінченно малих мас, буде мати нескінченне число ступенів свободи.

Для визначення ступеня свободи системи необхідно кожну масу системи закріпити зв'язками від усіх можливих переміщень. Кількість стержнів, що вводяться, і визначає ступінь свободи системи.

m1

Маса рами мала в порівнянні з зосередженими масами, тому нею зневажають.

m2

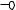
Ст. свободи = 6

Якщо зневажити поворотами мас і вважати їх точковими.

 

У практичних розрахунках часто зневажають

m1

переміщеннями мас за рахунок розтягання чи

 

стиску стержнів, тоді

m2

m1

ст. свободи = 4

m2

m1

ст. свободи =3

ст. свободи =1

Методи динаміки споруд

У динаміці споруд використовують два основних методи досліджень:

1.Кінематичний метод, суть якого полягає в тім, що конструкція в кожен момент часу розглядається в рівновазі під дією заданих динамічних навантажень і сил інерції всіх її мас.

2.Енергетичний метод заснований на дослідженні повної потенційної енергії системи

зурахуванням інерційних сил.

Лекція 13

Коливання систем з одним ступенем свободи

Розглянемо систему з одним ступенем свободи у виді невагомої балки з зосередженою масою m.

a

m

Уст.

Рис. 1

Уст - прогин балки в місці додатка маси при її статичній дії Нехай на балку діє динамічне навантаження Р (t).

Уст m

P(t)

У - прогин з початкового

 

 

деформованого стану

 

 

за рахунок дії

y

 

динамічного навантаження

Рис. 2

 

 

Для висновку диференціального рівняння руху маси використовуємо кинетостатический метод. Розглянемо випадок руху маси униз від стійкого стану (мал. 2).

Покажемо окремо балку і масу з діючими на неї силами.

d2 y m dt2

a P m

R P(t)

Рис. 3

R - реакція балки, що намагається повернути балку у вихідний стан Р - сила опору руху маси

md22y - сила інерції маси, що спрямована протилежно прискоренню маси. dt

На підставі принципу Даламбера, умова динамічної рівноваги маси запишеться:

 

 

d2 y

 

 

у 0;

 

R m dt2

P

(1)

Запишемо переміщення маси m через прогин балки:

y 11R 1P(t)

(2)

де 11 - переміщення балки в місці положення маси m від сили Р=1, прикладеної по напрямку руху маси;

1P(t) - аналогічне переміщення від заданого динамічного навантаження.

P=1

 

P(t)

11

1P(t)

a

З вираження (2) визначимо реакцію балки R

R

 

y

 

 

 

1P(t)

 

 

 

 

11

 

 

11

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Підставляємо вираження (3) у (1)

 

 

 

 

m

d2 y

 

P

 

y

 

 

 

dt2

 

 

 

 

розділимо це рівняння на m

 

 

 

 

11

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

d 2 y

 

P

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dt2

m

m

 

 

 

позначимо

 

 

 

 

11

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

1

 

 

 

 

 

 

 

 

 

 

m 11

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1P(t)

11

1P(t ) m 11

(3)

(4)

(5)

Тоді загальне диференціальне рівняння руху системи з одним ступенем свободи запишеться:

 

d 2 y

 

P

 

 

 

 

2 y

 

2

1P(t )

(6)

 

dt2

 

 

 

m

 

 

 

 

 

 

 

 

Лекція 14

Вільні коливання систем без обліку їх сил опору

Вільні коливання систем з одним ступенем свободи без обліку їх сил опору визначаються по вираженню:

Р=0;

P(t) = 0

1P(t) = 0

 

 

d2 y

 

2 y 0

 

(7)

 

dt2

 

 

 

 

 

Рішення диференціального рівняння (7):

 

 

 

y

A sin t B cos t

(8)

З вираження (8) видно, що вільні коливання системи відбуваються по гармонійному

законі.

Розглянемо для аналогії рух точки по колі радіуса С, з постійною кутовою швидкістю

y

 

A = c cos

K1

B = c sin

t

K

y

C

 

y0 =B

 

A

x

 

 

Тоді

c cos sin t sin cos t c sin t

 

y

 

що відповідає положенню крапки К1 у момент часу t

 

 

 

 

 

 

 

 

y c sin t

(9)

Графік функції (9) y = f(t) являє собою синусоїду

 

y

 

T

 

y0=Csin

C

t

де: - зрушення фази;

С - амплітуда коливань;

 

 

Т - період коливань; - кругова

частота власних коливань.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

З вираження (5)

 

 

 

 

 

 

 

 

рад

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

сек

.

 

 

 

 

 

 

 

 

 

m 11

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Зосереджена маса через вагу записується

 

 

 

 

 

 

 

 

 

 

G = m g

чи

 

m

G

;

 

G

y

 

 

 

;

 

 

 

 

yст

,

 

 

 

 

ст

11

 

 

 

 

 

 

g

11

 

 

 

 

 

 

G

 

тоді:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

g G

 

 

 

 

 

 

чи

 

 

 

 

 

 

 

 

 

G

yст

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

g

 

 

 

 

 

 

 

 

 

(10)

 

 

 

 

 

 

 

 

 

yст

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Період коливань:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Т

 

2

 

 

 

 

 

 

 

 

 

 

 

 

(11)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

тобто час, за який відбувається цикл коливань.

Лекція 15

Змушені коливання систем з одним ступенем свободи при дії вібраційного навантаження

Вібраційне навантаження створюють машини з неврівноваженою обертовою частиною, маса якої має щодо осі обертання ексцентриситет .

m0

P

Psin t

Під час руху неврівноваженої маси виникає відцентрова сила, обумовлена по формулі

P m 2

 

(12)

0

 

 

де m0 - маса неврівноваженої частини, = кутова швидкість обертання маси m0.

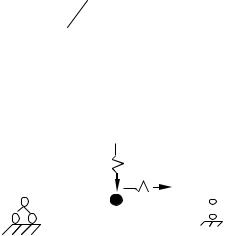
Якщо двигун робить n оборотів у хвилину, то кутова швидкість буде визначати і кругову частоту діючого навантаження

 

 

 

2 n

(13)

 

 

 

 

де n об

 

60

 

 

.

 

 

 

 

мин

 

 

 

 

 

Якщо початок дії навантаження вважати від горизонтальної осі, то складові

відцентрової сили будуть:

 

 

 

 

- вертикальна

 

Ру = Р sin t

 

- горизонтальна

Px = P cos t

 

Psin t

Pcos t

 

 

 

 

 

m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розглянемо дію сили Р sin t. Диференціальне рівняння (6) у цьому випадку

запишеться:

 

 

 

 

 

d 2 y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 y

2

 

 

,

 

 

 

1

 

 

 

 

dt 2

1P ( t )

 

 

 

 

 

 

 

 

 

 

 

 

 

де

2

;

 

 

1P(t )

11P sin t

 

 

 

 

 

 

 

 

 

тоді:

 

 

m 11

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

d 2

y

 

 

2 y

 

P sin t

(14)

 

 

 

 

 

d t 2

 

 

m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

де m - маса двигуна, включаючи і m0.

Повне рішення диференціального рівняння (14):

 

 

y = A sin t + B cos t + Ф

 

 

 

 

 

 

 

(15)

де

Ф = С + Д sin t

 

 

 

 

 

 

 

(16)

 

 

 

 

 

 

 

 

Ф

Д 2

sin t

 

 

 

 

 

 

 

 

підставляючи Ф и Ф’’ у рівняння (14) замість в і

d2 y

 

 

 

dt2

 

 

 

 

 

 

 

 

Д 2 sin t 2 С Д sin t

P

sin t

(17)

 

 

2С 0

 

 

 

m

 

 

при t = 0

так як 0

то С = 0

 

 

Підставляючи С = 0 і розділивши рівняння (17) на sin t, одержимо:

 

 

 

Д 2 2

Д

P

 

,

 

 

 

m

 

 

 

 

 

 

 

 

 

 

чи

 

Д

 

P

 

 

 

 

 

 

 

 

P

 

 

.

 

m 2 2

m

2

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

З вираження:

1

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

2

 

 

 

2m

 

 

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m

 

 

 

 

 

 

 

 

 

 

 

 

 

чи

11

 

 

 

 

 

 

 

 

11

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P 1 1

 

 

 

 

 

 

 

 

Д

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

тоді:

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P 11

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ф

 

sin t

 

 

 

(18)

 

2

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Загальне рішення диференціального рівняння (14) запишеться:

 

 

y Asin t Bcos t

 

P 11

 

sin t

 

 

 

(19)

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

I

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 2

II

Повне рішення складається з 2х частин. I частина являє собою рішення однорідного диференціального рівняння і характеризує вільні коливання системи. При наявності самих незначних сил опору вільні коливання системи швидко загасають і залишається IIя частина рівняння, що являє собою сталі змушені коливання при дії вібраційного навантаження.

У дин

P 11

sin t

(20)

2

 

 

 

 

1 2

Якщо позначити Уст(Р) = Р 11 - прогин від максимального динамічного навантаження, при статичній її дії, то

 

У дин

 

У ст ( Р )

 

 

sin t

(21)

2

 

 

 

 

1

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

Максимальний динамічний прогин одержимо в тому випадку, якщо sin t

1 :

 

У m ax дин

 

 

У ст ( Р )

 

 

 

1

2

 

 

 

 

 

 

позначимо:

 

 

2

 

 

 

 

К дин

 

 

1

 

 

 

 

 

 

 

 

(22)

 

1

 

 

 

2

 

 

 

 

 

 

 

 

2

 

 

 

 

де Кдин - динамічний коефіцієнт при дії вібраційного навантаження

Удинmax Кдин Уст

Знаючи Кдин ми можемо розраховувати систему на динамічне навантаження як на статичне, якщо її попередньо помножити на Кдин, тобто

КдинP sin t

Побудуємо графік зміни динамічного коефіцієнта (по абсолютній величині) у

залежності відносини , де - частота власних коливань; - змушені коливання.

[kдин]

=0; kд=1

4

 

;kд

 

область резонансу

3

2

1

0.5

1

1.5

2

2.5

/

Рис. 1

y

t

Рис. 2. Графік наростання коливань при резонансі

З мал.1 і мал.2 видно, що якщо частота сили, що змушує, наближається до частоти

вільних коливань, то настає явище резонансу. Резонансною вважається область 07,

 

13,.

 

При резонансі коливання необмежено зростають, що на практиці приводить до руйнування споруди.

З огляду на сказане, у динамічних розрахунках завжди необхідно визначати частоту вільних коливань і порівнювати її з частотою сили, що змушує. Необхідно щоб частота змушених коливань була менше частоти вільних коливань , у противному випадку при зупинці і пуску двигуна можливе явище резонансу.

На практиці потрібно, щоб 07, .

Для дотримання цієї умови звичайно змінюють частоту вільних коливань

 

g

 

 

,

Уст

тому що частоту змушених коливань у більшості випадків змінити не можна.

Частота збільшується при збільшенні жорсткості споруди, зменшенні довжин прольотів і т.п.

Лекція 16

Вільні коливання систем із двома ступенями свободи

Системи з двома ступенями свободи є часткою случаємо систем з декількома ступенями свободи. Але ці системи є найпростішими, що дозволяють ще одержати в кінцевому виді розрахункові формули для визначення частот коливань, амплітуд і динамічних прогинів.

d2 y

d2 y

2

 

 

 

 

 

 

 

 

 

 

 

 

1

m2 dt2

 

 

 

 

 

 

 

 

 

 

 

 

m1 dt2

 

 

 

 

 

 

 

 

 

 

 

 

 

m1

m2

x

 

 

 

 

 

 

 

 

 

 

 

 

y1

y2

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

Прогини балки від дії

 

 

 

інерційних сил:

P1=1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

11

21

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

d2 y

11 m2

d2 y

12

 

 

y1 m1

dt

21

dt

22

 

P2=1

 

 

 

 

 

 

 

 

 

 

(1)

 

 

 

 

d2 y

 

 

 

d2 y

 

 

 

y

 

m

 

 

m

 

 

 

 

2

 

1

21

 

 

2

22

 

 

 

1

dt

2

 

2

dt

2

 

 

 

 

 

 

 

 

 

 

 

 

 

12

22

 

 

 

 

 

 

 

 

 

 

 

 

 

Знаки (-) у вираженнях (1) викликані тим, що інерційні сили й од. переміщення мають протилежний напрямок.

Вважаємо, що коливання мас відбуваються по гармонійному законі:

 

 

A1 sin t

y1

 

2

A

2

 

 

 

 

y

 

 

sin t

 

Знайдемо прискорення руху мас:

d 2

y

1

 

A1

2 s in t

 

 

 

 

d t

2

 

 

 

 

 

 

 

 

 

 

 

 

y 2

 

 

 

 

 

 

d 2

 

 

A 2

2

s in t

 

 

d t

2

 

 

 

 

 

 

 

 

 

 

 

 

(2)

(3)

Підставляючи вираження (2) і (3) у рівняння (1) одержимо:

A sin t m

 

A 2

sin t

m

 

 

A 2

sin t

 

 

1

1

11

 

1

 

 

2

 

12

 

2

 

 

(4)

 

 

 

 

 

 

A 2

sin t m

 

 

 

 

A 2

sin t

A sin t m

21

 

22

 

 

2

1

 

1

 

 

2

 

2

 

 

 

чи

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

2

 

 

 

 

 

 

 

 

m1 11 A1 m2 12 A2

 

 

 

 

 

 

 

 

 

 

A1

 

 

 

 

 

 

 

 

(5)

 

 

 

 

 

 

 

2

 

 

2

 

 

 

 

 

 

 

m1 21 A1 m2 22

A2

 

 

 

 

 

 

 

 

 

A2

 

 

 

 

 

 

 

 

Невідомими вважаємо амплітуди коливань А1 і А2, перетворимо рівняння:

 

m1 11

2

1 m2 12

2

А2 0

 

 

 

 

 

 

(6)

 

 

2

A

 

m

 

 

A

 

2 1

 

А

 

m

22

2

0

 

1

21

 

1

2

 

2

 

 

 

 

 

Рішення системи однорідних рівнянь А1 = А2 =0 нас не влаштовує, щоб одержати не нульове рішення прирівняємо нулю детермінант системи (6):

Д

m1 11 2 1

m2 12 2 А2

 

0

(7)

m1 21 2 A1 m2 22 A2 2 1 А2

 

 

 

чи

 

 

 

 

 

m1 11 2 1 m1 22 2 1 m1m2 12

2 4

0

(8)

перетворимо рівняння (8), вважаючи невідомої кругову частоту власних коливань :

m1m2 122 22 4 m1 122 2 m2 22 2 1 m1m2 122 4 0

m1m2 12 22 122 4 m1 11 m2 22 2 1 0

(9)

 

 

Рівняння (9) називається бігармоничним рівнянням вільних коливань систем із двома ступенями свободи.

Заміняючи перемінну 2 = Z, одержимо

Z1,2

m1 11 m2 22

m1 11 m2 22 2 4m1m2 11 22 122

(10)

 

2m1m2 11 22 122

звідси визначаємо Z1 і Z2.

І далі:

1

 

Z1

 

;

2

 

 

Z2

 

;

У результаті можна зробити наступні висновки:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности