2.4. Направленность взаимосвязи

Диаграмма рассеяния на рис. 3.4, кроме сильной статистической взаимосвязи, имеет еще одну особенность – прямо пропорциональную тенденцию зависимости. Это значит, что улучшение, например, результата в толкании ядра весом 3 кг вызывает улучшение (в среднем) результата в толкании ядра весом 5 кг. На рис. 3.5 представлена диаграмма обратно пропорциональной зависимости. В этом случае увеличение одного показателя связано с уменьшением другого (в среднем). Направленность зависимости отражается в знаке коэффициента корреляции. Знак «+» указывает на прямую пропорциональную или положительную взаимосвязь; знак « – » говорит об обратной или отрицательной взаимосвязи (рис. 3.6).

а

б

в

г

д

Рис. 3.6. Примеры статистических взаимосвязей:

а) нелинейная форма зависимости, б) отсутствие статистической зависимости (коэффициент корреляции = 0), в)функциональная зависимость(коэффициент корреляции = +1), г)положительная зависимость (коэффициент корреляции > 0), д)отрицательная зависимость (коэффициент корреляции < 0).

2.5. Методы вычисления коэффициентов взаимосвязи

Величина коэффициента взаимосвязи рассчитывается с учетом шкалы, использованной для измерений.

Для оценки взаимосвязи, когда измерения производят в шкале отношений или интервалов и форма взаимосвязи линейная, используется коэффициент корреляции Бравэ-Пирсона (коэффициенты корреляции для других шкал измерения в данном пособии не рассматриваются). Обозначается он латинской буквой – r. Вычисление значения r чаще всего производят по формуле:

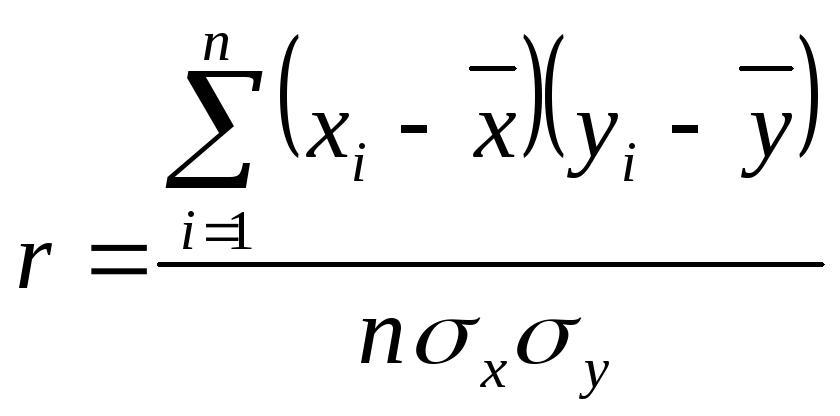, (3.1)

где и– средние арифметические значения показателейx и y, и– средние квадратические отклонения,n – число измерений (испытуемых).

В некоторых случаях тесноту взаимосвязи определяют на основании коэффициента детерминации D, который вычисляется по формуле:

. (3.2)

Этот коэффициент определяет часть общей вариации одного показателя, которая объясняется вариацией другого показателя. Так, для вычисленного значения r = –0,677 коэффициент детерминации определится так:

.

Следовательно, только на 45,8 % распределение спортивного результата в тройном прыжке объясняется результатам в беге на 30 м. Остальная часть (100% – 45,8% = 54,2%) вариации объясняется влиянием других неучтенных факторов.

Рис. 3.7. Зависимость между результатами в беге на 30 м с ходу и тройном прыжке с места (n = 10).

3. Основы теории проверки статистических гипотез

В физическом воспитании и спорте часто приходится делать вывод об общих закономерностях проявления какого-либо показателя: нормально или нет распределены результаты измерений этого показателя в генеральной совокупности, отличается ли среднее арифметическое значение результатов измерения в генеральной совокупности до тренировок от аналогичного параметра после тренировок (эффективна или нет методика тренировок), отличается ли дисперсия генеральной совокупности результатов измерения показателя до тренировок от такого же показателя после тренировок (изменилась или нет стабильность результатов спортсмена) и т.д.

Так как указанные выводы делаются на основании относительно небольшого числа результатов измерения показателя (n = 30), необходима проверка достоверности (бесспорности) таких выводов.

Для этого применяются статистические гипотезы.

Статистической гипотезой называется проверяемое математическими методами предположение относительно статистических характеристик результатов измерений. Статистическую гипотезу обозначают символом H.

Обычно выдвигают и проверяют две противоречащие друг другу гипотезы:

1. нулевую (основную) H₀;

2. конкурирующую (альтернативную) H₁.

Примеры статистических гипотез:

1. Нулевая гипотеза H₀: закон распределения результатов измерения является нормальным. Конкурирующая гипотеза H₁: закон распределения результатов измерения отличен от нормального.

2. Нулевая гипотеза H₀: среднее арифметическое значение генеральной совокупности результатов измерения показателя после цикла тренировок не изменилось. Конкурирующая гипотеза H₁: среднее арифметическое значение увеличилось.