9. Стандартная ошибка среднего арифметического
Чтобы судить о том, насколько точно проведенные измерения отражают состав генеральной совокупности, необходимо вычислить стандартную ошибку средней арифметической выборочной совокупности.
Стандартная ошибка средней арифметической характеризует степень отклонения выборочной средней арифметической от средней арифметической генеральной совокупности.
Стандартная ошибка средней арифметической вычисляется по формуле:
,
где – стандартное отклонение результатов измерений, n – объем выборки.
Зачастую мы имеем дело с одной случайной выборкой и с одной полученной при ее обработке выборочной средней. Задача заключается в суждении о величине неизвестной генеральной средней по полученной неточной величине случайной выборочной средней.
Вычислим среднюю ошибку найденного выборочного среднего значения роста:
195
см; σ = 8,8 см;
см.
2,8 см составляют не максимальную, а среднюю возможную ошибку среднего. Отдельные выборочные средние могут отклоняться от генеральной как больше, так и меньше, чем на 2,8 см.
Каковы же пределы возможных ошибок случайной выборки, какова ее максимальная ошибка? Величина максимальной ошибки зависит от величины средней ошибки и вычисляется по формуле
.
При объеме выборки n = 10:
.
Все
случайные выборочные средние, которые
могут быть получены в подобных опытах
(в том числе и фактически полученная
выборочная средняя
= 195 см), при своем варьировании около
неизвестного генерального среднего в
подавляющем количестве группируются
около него так, что лишь ничтожный
процент их отклоняется от генеральной
средней более, чем на величину максимальной
ошибки.
Другими словами, генеральная средняя определяется как
.
Эти пределы колебаний значительно сужаются, если средняя ошибка уменьшается благодаря увеличению численности выборки.
Искомая
генеральная средняя лежит между
и
.
Таким образом, при высокой точности
выполнения эксперимента и достаточно
большом числе измерений можно определить
среднюю арифметическую бесконечно
большого числа экспериментов.
До сих пор мы определяли максимальную ошибку выборочной средней, исходя из того, что все остальные показатели известны. Если же мы хотим достичь определенной точности, определенного приближения к генеральной средней, в этом случае встает вопрос о численности выборки (о том, сколько измерений, опытов необходимо провести).
Допустим, что максимальная ошибка должна быть равна 5 см. Сколько человек надо обследовать (измерить) в нашем случае?
.
Следовательно, мы должны провести измерения роста у 36 баскетболистов высокого класса.
10. Достоверность различий
Следующим важным вопросом практически для каждого экспериментатора является умение доказать достоверность различий между двумя рядами признаков.
Проверку достоверности различия двух рядов измерений производят путем вычисления критерия достоверности различия – t:
,
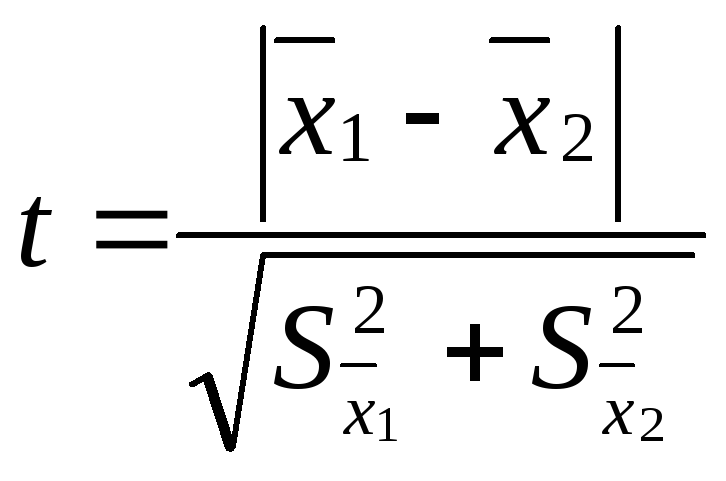где
– средняя одной выборки;
– средняя другой выборки;
– средняя ошибка первой выборки;
– второй выборки. Если t < 2, то различие
между двумя выборками считается
недостоверным, если t
2, то различие между двумя выборками
достоверно на 95%.