Лабораторна робота № 9 Чисельне розв’язання звичайних диференційних рівнянь Теоретичні відомості

Звичайні диференційні рівняння (ЗДР) широко застосовуються для математичного моделювання процесів та явищ в різних галузях науки та техніки. Перехідні процеси в радіотехніці, кінетика хімічних реакцій, динаміка біологічних популяцій, рух космічних об’єктів, моделі економічного розвитку досліджуються за допомогою ЗДР.

До диференційного рівняння n-го порядку як невідомі величини входять функція і її першіn похідних по аргументу x:

(9.33)

Рівняння (9.33) еквівалентно системі n рівнянь першого порядку

,

(9.34)

де k=1, 2,… , n.

Рівняння (9.33) і еквівалентна йому система (9.34) мають безліч розв’язків. Єдині розв’язкі відокремлюють за допомогою додаткових умов, котрим повинні задовольняти шукані розв’язкі. В залежності від виду таких умов розглядають три типа задач, для яких доведено існування та єдність розв’язків.

Перший тип – це задачі Коши, або задачі з початковими умовами. Для таких задач крім початкового рівняння (9.33) в будь-якої точці повинні бути задані початкові умови, тобто значення функціїта її похідних

..., .

Для системи ЗДР типа (9.34) початкові умови задаються у вигляді

, , ...,.

(9.35)

До другого типу задач відносяться так звані граничні або крайові задачі, в яких додаткові умови задаються у вигляді функціональних співвідношень між шуканими розв’язками. Кількість умов повинна співпадати з порядком n-го рівняння або системи. Якщо розв’язок задачі визначається в інтерваліxє[x₀,x_k], то такі умови можуть бути задані як на межах, так і в інтервалі. Мінімальний порядок ЗДР, для яких може бути сформульована гранична задача, дорівнює двом.

Третій тип задач для ЗДР – це задачі на власні значення. Такі задачі відрізняються тим, що окрім шуканих функцій та їх похідних до рівняння входять додатковоmневідомих параметрів12які називаються власними значеннямиДля єдності розв’язка на інтервалі [x₀x_k] необхідно задатиm+nграничних умовЯк приклад можна назвати задачі визначення власних частоткоефіцієнтів дисипаціїструктури електромагнітних полів і механічних напружень в коливальних системахзадачі знаходження фазових коефіцієнтівкоефіцієнтів затуханнярозподілення напруженостей полів хвильових процесів, тощо

Методи наближеного інтегрування диференційних рівнянь можна умовно поділити на три групи:

• аналітичні, які дозволяють одержати розв'язок у вигляді аналітичного вираження;

• графічні, які дають наближений розв'язок у вигляді графіка;

• чисельні, які дають наближений розв'язок у вигляді таблиці.

До чисельного розв'язку ЗДР приходиться звертатися коли не вдається побудувати аналітичний розв'язок задачі через відомі функції Хоча для деяких задач чисельні методи є більш ефективними навіть при наявності аналітичних розв'язків

Метод Ейлера

Дано звичайне диференційне рівняння (ЗДР) першого порядку

.

(9.36)

Необхідно знайти розв’язок цього рівняння , яке задовольняє початковій умові

.

(9.37)

Така задача називається задачею Коші.

Чисельний розв’язок задачі Коші полягає у находженні значень в точкахвідрізка, деh– крок інтегрування; .

Якщо нанести точки на площинуXOY і з’єднати їх відрізками прямої, можна одержати ломану лінію, яка називається ломаною Ейлера, – наближене зображення кривої.

Позначимо ;,.

Змінимо похідну в (1) – відношенням кінцевих різниць

,

(9.38)

.

При маємоабо.

При маємоабо.

Для наступних значень x маємо

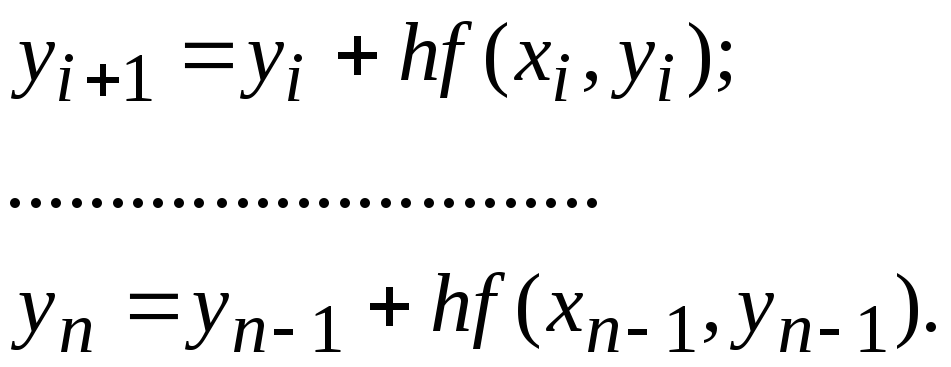
Таким чином, одержимо таблицю значень у відповідних точках, яка є грубим наближенням розв’язку ЗДР.

Метод Ейлера найпростіший і порівняльно грубий чисельний метод інтегрування.

Приклад 9.1.

Розв’язати диференційне рівняння в інтервалі.