Билет 11.

1. Достаточные признаки сходимости знакоположительных рядов: признак сравнения в конечной и предельной формах

1) В КОНЕЧНОЙ Если , и ряд сходится, то сходится и ряд .Если , и ряд расходится, то расходится и ряд .

2) В ПРЕДЕЛЬНОЙ Если заданы ряды и существует , то ряды сходятся либо расходятся одновременно.

Пример: 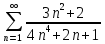; исследуем по признаку сравнения в предельной форме:

2. Непрерывная случайная величина. Функция и плотность распределения, их свойства

Непрерывная СВ может принимать любое значение из некоторого промежутка или на всей числовой прямой. Перечислить все значения или задать с помощью таблицы НСВ невозможно. Ее можно определить с помощью задания функции распределения: F(x)=P(X<x). Эта функция не имеет скачков. Свойства ф. распределения: 1) 0≤F(x) ≤1; 2) F(-∞)=0; F(+∞)=1; 3) F(x1) ≤F(x2) – функция постоянная или возрастает; 4) P(a<X<b)=F(b)-F(a). НСВ также можно задать с помощьюплотности распределения: f(x)=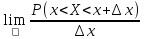; f(x)=F’(x). Свойства плотности распр.: 1) f(x) ≥0; 2) 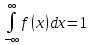; 3)P(a<X<b) = 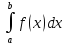; 4)F(x)=;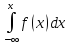

Пример: Дана функция распределения, найти вероятность того, что в результате испытания случайная величина Х примет значение, заключенное в интервале (0;2). F(x)=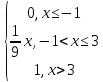 P(0<X<2)=F(2)-F(0)=1/2.

Билет 12.

12. Достаточные признаки сходимости знакоположительных рядов: признак Даламбера

Если существует то:   при ряд сходится;  при ряд расходится.

ПРИМЕР  

Таким образом, ряд сходится.

Радикальный признак Коши Если существует то:  при ряд сходится; при ряд расходится. ПРИМЕР Исследовать знакопол. числовой ряд 

Следовательно, ряд сходится.

Интегральный признак Коши Пусть задан ряд  члены которого являются значениями непрерывной, положительной и монотонно убывающей функции f(x) на промежутке . Тогда ряд сходится, если сходится несобственный интеграл . Если же расходится, то ряд также будет расходящимся.

ПРИМЕР

. Она положительная, непрерывная и убывающая на интервале.Она отрицательная на промежутке.

Таким образом, функция  

2. Числовые характеристики непрерывной случайной величины

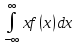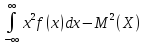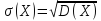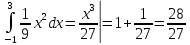Числовыми характеристиками НСВ являются мода, мат.ожидание, дисперсия, среднее квадратическое отклонение. Мода НСВ – такое возможное значение этой величины, при котором плотность распределения f(x) достигает абсолютного максимума. Мат.ожидание – M(X)=; Дисперсия – D(X) = ;.Пример: Дана плотность распределения, найти мат.ожидание и дисперсию. f(x)=. M(X) = ;D(X) = .

Билет 13.

1. Знакочередующие ряды. Признак Лейбница

Пусть для знакочередующегося ряда выполняются следующие условия: (монотонное убывание {a_n}) Тогда этот ряд сходится.

ПРИМЕР .

. гармонический ряди воспользуемся вторым признаком сравнения:

Таким образом, ряд из модулей

 - расходящийся.

ряд сходится, так как выполняются условия признака Лейбница: последовательностьмонотонно убывает и.

Следовательно, исходный ряд условно сходящийся.

Абсолютная сходимость

Знакопеременный ряд называют абсолютно сходящимся, если сходится ряд . Если ряд сходится, а ряд расходится, то ряд называют сходящимся условно. Очевидно, что если ряд сходится, то ряд также сходится. Обратное утверждение в общем случае неверно.