
- •Билет 1.
- •1. Понятие функции нескольких переменных. Частные производные первого порядка
- •2. Теоремы сложения вероятностей для несовместных и совместных событий
- •Билет 2.
- •1. Полный дифференциал функции нескольких переменных и его применение
- •2. Зависимые и независимые события. Условная вероятность. Теорема умножения вероятностей
- •Билет 3.
- •1. Градиент функции нескольких переменных
- •2. Теорема сложения вероятностей для совместных событий. Вероятность появления хотя бы одного события
- •Билет 4.
- •1. Частные производные и дифференциалы высших порядков
- •2. Формула полной вероятности. Вероятность гипотез. Формулы Байеса
- •Билет 5.
- •1. Локальный экстремум функции двух переменных
- •Билет 6.
- •1. Условный экстремум
- •2. Предельные теоремы в схеме Бернулли
- •Билет 7.
- •1.Наибольшее и наименьшее значение функции в замкнутой области
- •2. Закон распределения вероятностей дискретной случайной величины. Функция распределения
- •Билет 8.
- •1.Метод наименьших квадратов
- •2. Математическое ожидание дискретной случайной величины и его свойства
- •Билет 9.
- •1.Числовые ряды. Основные понятия. Сходимость ряда. Свойства сходящихся рядов
- •2. Дисперсия дискретной случайной величины и ее свойства. Среднее квадратическое отклонение
- •Билет 10.
- •1.Необходимый признак сходимости. Гармонический ряд
- •2. Частные виды дискретных случайных величин: биномиальное распределение, распределение Пуассона, геометрическое распределение
- •Билет 11.
- •1. Достаточные признаки сходимости знакоположительных рядов: признак сравнения в конечной и предельной формах
- •2. Непрерывная случайная величина. Функция и плотность распределения, их свойства
- •Билет 12.
- •12. Достаточные признаки сходимости знакоположительных рядов: признак Даламбера
- •2. Числовые характеристики непрерывной случайной величины
- •Билет 13.
- •1. Знакочередующие ряды. Признак Лейбница
- •2. Равномерное распределение.Показательное распределение
- •Билет 14.
- •1. Степенные ряды. Область сходимости степенного ряда
- •2. Нормальное распределение. Правило трех сигм
- •Билет 15.
- •1. Ряд Маклорена. Разложение в ряд Маклорена некоторых элементарных функций
- •2. Дискретная двумерная случайная величина
- •Билет 16.
- •2. Числовые характеристики двумерной случайной величины. Корреляционный момент. Коэффициент корреляции
- •Билет 18.
- •1. Однородные ду первого порядка
- •2. Условные числовые характеристики системы случайных величин. Регрессия
- •Билет 19.
- •1. Линейные ду первого порядка
- •2. Линейная регрессия. Прямые линии среднеквадратической регрессии
- •Билет 20.
- •1. Ду второго порядка, допускающие понижение порядка
- •2. Выборочный метод. Эмпирическая функция распределения. Полигон и гистограмма
- •Билет 21.
- •1. Линейные ду второго порядка. Теоремы о структуре общего решения однородного и неоднородного уравнения
- •2. Точечные оценки параметров
- •Билет 22.
- •1. Линейные однородные ду второго порядка с постоянными коэффициентами
- •2. Методы получения точечных оценок: метод моментов, метод наибольшего правдоподобия
- •Билет 23.
- •2. Проверка статистических гипотез
- •Билет 25.
- •1. Элементыкомбинаторики. Классическое,статистическое и геометрическое
- •2. Критерий согласия Пирсона для проверки гипотезы о законе распределения наблюдаемой случайной величины
- •Билет 26.
- •1. Алгебра событий
- •2. Элементы теории корреляции. Выборочное уравнение прямой линии регрессии
2. Предельные теоремы в схеме Бернулли
Случай,
когда в схеме Бернулли число испытаний
велико или же вероятность появления
события А очень маленькая, вычисления
по формуле Бернулли затруднительные.
Поэтому для вычисления используются
предельные теоремы : 1) р<0,1, npq<9
– формула
Пуассона
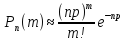 ;
2)
р>0,1, npq>9
– Локальная
формула Лапласа
;
2)
р>0,1, npq>9
– Локальная
формула Лапласа
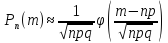 ;
3) вероятность того, что в серии изn
испытаний событие произойдет m1≤m≤m2
раз – Интегральная
формула Лапласа
;
3) вероятность того, что в серии изn
испытаний событие произойдет m1≤m≤m2
раз – Интегральная
формула Лапласа
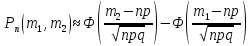 .
.
Пример:
Найти
вероятность того, что событие наступит
80 раз в 400 испытаниях, если вероятность
события в каждом испытании равна 0,2. По
локальной формуле Лапласа:
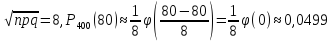
Билет 7.
1.Наибольшее и наименьшее значение функции в замкнутой области
Для того, чтобы найти наибольшее и наименьшее значения функции z=f (х, у), непрерывной в ограниченной замкнутой области D, необходимо воспользоваться следующим правилом:
1) Найти критические точки данной функции, лежащие в области D и вычислить значения функции в этих точках (не классифицируя экстремума).
2)Найти наибольшее и наименьшее значения функции на линиях, образующих границу области.
3)Из всех полученных значений выбрать наибольшее и наименьшее.
Пример:
Найти
наиб и наим знач ф-ции
z = x2 +
2xy -
4x +
8y
в прямоуголь, огранич прямыми
х = 0, у = 0, х = 1, у = 2.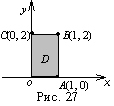
а) частные производные данной функции:
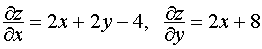 .
.Приравн их к 0, получ сист ур-ний для нахожд коорд крит точек:
![]() или
или
![]()
Отсюда: х = -4, у = 6., M0(-4, 6)– критическая точка, не принадлежащая области D
б) Найдём наиб и наим знач ф-ции на каждой из линий, образующих границу области.
На отрезке ОА, у = 0, имеем z (x,0) = x2 - 4x. Так как z′= 2x - 4 = 0 при х = 2 и точка не принадлежит отрезку [ 0, 1] , то, вычисляя значения z (х, 0) на его концах, получаем: z (0, 0) = 0, z (1, 0) = -3.
АВ, где х = 1, имеем: z (1, у) = 1+2у-4+8у =10у -3, z′ = 10 > 0. Отсюда следует, что функция
z = 10у-3для у ![]() [
0, 2] всюду возрастает, следовательно,
достигает наибольшего и наименьшего
значений на концах отрезкаАВ:
z (1, 0) = - 3, z (1, 2) = 17.
[
0, 2] всюду возрастает, следовательно,
достигает наибольшего и наименьшего
значений на концах отрезкаАВ:
z (1, 0) = - 3, z (1, 2) = 17.
ВС (прямая у = 2) имеем z (х, 2) = x2 +16. Тогда z′ = 2x = 0 при х = 0, то есть критическая точка совпадает с точкой С. Поэтому вычислим значения функции z = x2 +16 лишь на концах отрезка ВС: z (0, 2) = 16, z (1, 2) = 17.
ОС, где х = 0, имеем: z = 8у, z′ = 8 > 0. Таким образом, функция z = 8у возрастает на отрезке [ 0, 2] и достигает наибольшего и наименьшего значений на концах отрезка ОС: z (0, 0) = 0, z (0, 2) = 16.
в) Выбирая из всех полученных значений исходной функции наибольшее и наименьшее, имеем zнаиб(1, 2) = 17, zнаим(1, 0) = -3.
2. Закон распределения вероятностей дискретной случайной величины. Функция распределения
Случайная величина – величина, которая в результате испытания принимает значение, заранее неизвестное. ДСВ – принимает изолированные друг от друга значения (подбрасывание кубика). Закон распределения вероятностей ДСВ – соответствие между возможными значениями СВ и вероятностями. Он может быть задан при помощи формулы, таблицы или графика.
Пример: В цехе 2 станка, вероятность безотказной работы в течении часа равна 0,6. Составить закон распределения и построить многоугольник распределения.
Р(Х=0)=Р2(0)=С20р0q2=0,16.
Построить график.
Распределение
вероятностей можно так же задать при
помощи задания функции
распределения
– вероятность того, что СВ будет меньше
х: F(x)=P(X<x).
Геометрический
смысл функции распределения:
значение функции в точке х равняется
возможности того, что значения СВ будут
лежать левее точки х на числовой оси.
______х______>
Для
ДСВ значения функции распределения по
известной таблице можно найти с помощью
формулы F(x)=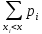 .
.
Пример:
1)
х<0, F(x)=0;
2) 0<x≤1,
F(x)
= 0,16; 3) 1<x≤2,
F(x)
= 0,64; 4) x>2,
F(x)
= 1.
 График
функции распределения имеет ступенчатый
вид. Свойства функции: 1) 0≤F(x)≤1;
2) неубывающая функция ; 3) непрерывна
слева; 4) F(-∞)=0,
F(+∞)=1;
5) P(a≤X≤b)=F(b)-F(a).
График
функции распределения имеет ступенчатый
вид. Свойства функции: 1) 0≤F(x)≤1;
2) неубывающая функция ; 3) непрерывна
слева; 4) F(-∞)=0,
F(+∞)=1;
5) P(a≤X≤b)=F(b)-F(a).
