
- •Билет 1.
- •1. Понятие функции нескольких переменных. Частные производные первого порядка
- •2. Теоремы сложения вероятностей для несовместных и совместных событий
- •Билет 2.
- •1. Полный дифференциал функции нескольких переменных и его применение
- •2. Зависимые и независимые события. Условная вероятность. Теорема умножения вероятностей
- •Билет 3.
- •1. Градиент функции нескольких переменных
- •2. Теорема сложения вероятностей для совместных событий. Вероятность появления хотя бы одного события
- •Билет 4.
- •1. Частные производные и дифференциалы высших порядков
- •2. Формула полной вероятности. Вероятность гипотез. Формулы Байеса
- •Билет 5.
- •1. Локальный экстремум функции двух переменных
- •Билет 6.
- •1. Условный экстремум
- •2. Предельные теоремы в схеме Бернулли
- •Билет 7.
- •1.Наибольшее и наименьшее значение функции в замкнутой области
- •2. Закон распределения вероятностей дискретной случайной величины. Функция распределения
- •Билет 8.
- •1.Метод наименьших квадратов
- •2. Математическое ожидание дискретной случайной величины и его свойства
- •Билет 9.
- •1.Числовые ряды. Основные понятия. Сходимость ряда. Свойства сходящихся рядов
- •2. Дисперсия дискретной случайной величины и ее свойства. Среднее квадратическое отклонение
- •Билет 10.
- •1.Необходимый признак сходимости. Гармонический ряд
- •2. Частные виды дискретных случайных величин: биномиальное распределение, распределение Пуассона, геометрическое распределение
- •Билет 11.
- •1. Достаточные признаки сходимости знакоположительных рядов: признак сравнения в конечной и предельной формах
- •2. Непрерывная случайная величина. Функция и плотность распределения, их свойства
- •Билет 12.
- •12. Достаточные признаки сходимости знакоположительных рядов: признак Даламбера
- •2. Числовые характеристики непрерывной случайной величины
- •Билет 13.
- •1. Знакочередующие ряды. Признак Лейбница
- •2. Равномерное распределение.Показательное распределение
- •Билет 14.
- •1. Степенные ряды. Область сходимости степенного ряда
- •2. Нормальное распределение. Правило трех сигм
- •Билет 15.
- •1. Ряд Маклорена. Разложение в ряд Маклорена некоторых элементарных функций
- •2. Дискретная двумерная случайная величина
- •Билет 16.
- •2. Числовые характеристики двумерной случайной величины. Корреляционный момент. Коэффициент корреляции
- •Билет 18.
- •1. Однородные ду первого порядка
- •2. Условные числовые характеристики системы случайных величин. Регрессия
- •Билет 19.
- •1. Линейные ду первого порядка
- •2. Линейная регрессия. Прямые линии среднеквадратической регрессии
- •Билет 20.
- •1. Ду второго порядка, допускающие понижение порядка
- •2. Выборочный метод. Эмпирическая функция распределения. Полигон и гистограмма
- •Билет 21.
- •1. Линейные ду второго порядка. Теоремы о структуре общего решения однородного и неоднородного уравнения
- •2. Точечные оценки параметров
- •Билет 22.
- •1. Линейные однородные ду второго порядка с постоянными коэффициентами
- •2. Методы получения точечных оценок: метод моментов, метод наибольшего правдоподобия
- •Билет 23.
- •2. Проверка статистических гипотез
- •Билет 25.
- •1. Элементыкомбинаторики. Классическое,статистическое и геометрическое
- •2. Критерий согласия Пирсона для проверки гипотезы о законе распределения наблюдаемой случайной величины
- •Билет 26.
- •1. Алгебра событий
- •2. Элементы теории корреляции. Выборочное уравнение прямой линии регрессии
Билет 8.
1.Метод наименьших квадратов
В основе метода наименьших квадратов (МНК) лежит поиск таких значений коэффициентов регрессии, при которых сумма квадратов отклонений теоретического распределения от эмпирического была бы наименьшей.
![]()
Пример: y=ax+b ; найти зависимость
|
xi |
1 |
2 |
3 |
4 |
5 |
6 |
|
yi |
-0.5 |
0.2 |
0.4 |
1 |
1.4 |
1.6 |
∑xi=1+2+3+4+5+6=21
∑xi2=12+22+32+42+52+62=91
∑yi=-0.5+0.2+0.4+1+1.4+1.6=4.4
∑xi yi=1*(-0.5)+2*0.2+3*0.4+4*1+5*1.4+6*1.6=23.5
Сист ур-ний
91a+21b=23.5
21a+6b=4.4
a*=∆i /∆=48.6/105≈0.46
b*=-93.1/105≈-0.89
y=0.46x-0.89
2. Математическое ожидание дискретной случайной величины и его свойства
Одной
из характеристик ДСВ является мат.
ожидание
- сумма произведений значений СВ на
соответствующие вероятности. M(X)= .Мат.
ожидание приблизительно равно среднему
значению величины. Свойства:
1) M(c)=c;
2) M(cX)=cM(X);
3) M(X1+…+Xn)=M(X1)+…M(Xn);
4) M(X+c)=M(X)+c;
5) M(X-Y)=M(X)-M(Y);
6) M(XY)=M(X)M(Y).
.Мат.
ожидание приблизительно равно среднему
значению величины. Свойства:
1) M(c)=c;
2) M(cX)=cM(X);
3) M(X1+…+Xn)=M(X1)+…M(Xn);
4) M(X+c)=M(X)+c;
5) M(X-Y)=M(X)-M(Y);
6) M(XY)=M(X)M(Y).
Пример: Найти мат.ожидание СВ, зная ее распределение
|
Х |
0 |
1 |
2 |
|
Р |
0,16 |
0,48 |
0,36 |
М(Х) = 0,48+2*0,36=1,2
Билет 9.
1.Числовые ряды. Основные понятия. Сходимость ряда. Свойства сходящихся рядов
Рядом
наз выражение вида U1+
U2+
U3+…=
Если члены ряда числа, то ряд наз числовым, если ф-ции – то функциональным.
Если все члены ряда явл полож числами, тогда ряд знакополож.
Если члены ряда имеют произвольный характер, тогда знакоперемен.
Частный случай знакопеременного ряда - знакочередующий
Ряд
называется сходящимся, если существует
конечный предел последовательности
частичных сумм
 ,
а числоS
называется суммой ряда.
,
а числоS
называется суммой ряда.
Если
последовательность не имеет конечного
предела, то говорят, что ряд расходится.
Однако в случае, когда
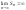 ,
говорят, что ряд имеет бесконечную
сумму.
,
говорят, что ряд имеет бесконечную
сумму.
Ряд
 называетсяn-ым
остатком ряда U1+
U2+
U3+…=
называетсяn-ым
остатком ряда U1+
U2+
U3+…=
СВОЙСТВА
1.Из
сходимости ряда (U1+U2+U3+…= )
следует сходимость ряда
)
следует сходимость ряда и обратно.
и обратно.
2.
Если сходится ряд (U1+U2+U3+…= )
и а
- некоторое действительное число, то
сходится и ряд
)
и а
- некоторое действительное число, то
сходится и ряд
 ,
и его сумма равнаaS,
т.е. справедливо равенство
,
и его сумма равнаaS,
т.е. справедливо равенство
 (здесьS
- сумма ряда).
(здесьS
- сумма ряда).
3.
Если сходятся ряды (U1+U2+U3+…= )
и
)
и
 ,
,
имеющие,
соответственно, суммы S
и ,
то сходится и ряд
 ,
причём сумма его равна (S
+).
,
причём сумма его равна (S
+).
4.
Необходимое условие сходимости ряда.
Если ряд (U1+U2+U3+…= )
сходится, то
)
сходится, то .
.
5. Ряд, составленный из элементов геометрической прогрессии
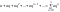 ,
,
сходится
при
 ,
причём
,
причём ,
и расходится при
,
и расходится при .
Его называют рядом бесконечной
геометрической прогрессии.
.
Его называют рядом бесконечной
геометрической прогрессии.
Пример:
Исследовать
на сходимость ряд
 Рассмотрим
Рассмотрим .
Ряд расходится, так как не выполняется
необходимое условие сходимости (
.
Ряд расходится, так как не выполняется
необходимое условие сходимости ( при
при )
)
