Встановлення закону зміни випадкових величин за результатами досліду і. Основні поняття та визначення теорії ймовірностей і математичної статистики

Випробуванням або дослідом називають реалізацію деяких правил, умов. Наприклад, випробуванням буде контроль придатності виробів прохідними і непрохідними калібрами, визначення величини розміру виробу, обробленого на верстаті. Явища, що виникають в результаті досліду, називають подіями. Подіями будуть: поява бракованого виробу при контролі калібрами, одержання певного розміру виробу при його вимірі. В теорії ймовірностей зазвичай розглядають масові досліди, тобто досліди, що виникають при незмінних основних умовах неодноразово.

Події поділяються на наступні.

1. Подія називається вірогідною, якщо в результаті даного досліду вона обов’язково відбудеться. Наприклад, поява бракованого зразка в партії бракованих виробів буде вірогідною подією.

2. Подія називається неможливою, якщо в результаті даного випробування вона відбутися не може. Наприклад, поява придатного зразка в партії непридатних деталей буде неможливою подією.

3. Подія називається випадковою (або можливою), якщо в результаті даного випробування вона може трапитись, але може і не трапитись. Наприклад, поява бракованого зразка в партії виготовлених виробів при невстановленому або невивченому технологічному процесі є випадковою (або можливою) подією.

4. Дві події називають несумісними, якщо при випробуванні поява однієї з них виключає можливість появи іншої. Наприклад, прохід прохідної та непрохідної сторін калібру під час перевірки придатної деталі є несумісними подіями.

5. Дві події називаються сумісними, якщо при випробуванні поява однієї з них не виключає можливість появи іншої. Наприклад, прохід прохідної і непрохідної сторін калібру під час контролю бракованої деталі є подія сумісна.

6. Події називаються єдино можливими, коли під час випробувань відбудеться хоч би одна з цих подій. Наприклад, під час контролю виробів калібрами єдино можливими подіями будуть поява або не поява бракованих виробів; для придатних виробів єдино можливими подіями є прохід через прохідний калібр і непрохід через непрохідний калібр.

7. Якщо при випробуванні можуть з’явитись декілька можливих подій, і при цьому немає підстав вважати, що поява однієї – більш можлива, ніж інших, то такі події називаються рівноможливими. Наприклад, партія виробів має в собі 10 пронумерованих бракованих виробів. При вийманні з партії деталей однієї у нас немає підстав вважати, що поява того чи іншого номера бракованого виробу більш можлива появи іншого номера. Поява бракованого виробу з тим чи іншим номером у даному випадку – подія рівноможлива.

Ймовірністю події називається відношення числа випадків, сприятливих для настання даної події, до всього числа несумісних, єдино можливих і рівноможливих подій

,

де P(A) – ймовірність події А;

m – число випадків, сприятливих для настання випадку А;

N – число несумісних, єдино можливих і рівноможливих подій.

Наприклад, нехай заданий допуск на діаметр 0,1. Вироби, що виходять за ці межі допуску, вважаються бракованими, а ті, що входять до поля допуску, – придатними. Уявимо, що партія, яка складається зN = 1000 виробів, має m₁ = 15 виробів, що виходять за верхню межу допуску, і m₂ = 18 виробів, які виходять за нижню межу допуску. У цьому випадку ймовірність появи в партії бракованих виробів під час випробування буде дорівнювати:

Якщо m = N, то –подія А вірогідна.

Якщо m = 0, то Р(А) = 0 – подія неможлива.

Випадковою величиною називають величину, котра в результаті досліду може набувати різні значення. Наприклад, можливість дістати з партії деталей бракований виріб є випадкова величина, яка може набувати значення „ + ” при появі бракованого виробу, і значення „ – ” при його відсутності. Величина розміру обробленого на верстаті придатного виробу є також випадкова величина, котра може набувати будь-яке значення в межах заданого поля допуску. Випадкові величини зазвичай позначають великими літерами, наприклад Х. Значення випадкової величини, котре вона набуває в результаті досліду, позначають малими літерами х₁, х₂,...х_n. При масових дослідах кожне з можливих значень випадкової величини х₁, х₂,...х_n може зустрітися m₁, m₂,…m_nраз. Ці числа називаються частотами. Якщо було проведено всього N випробувань, тобто , то відношенняназиваютьчастістю або відносною частотою.

Сукупність, що містить всі досліджувані вироби, називається генеральною сукупністю. Вибрані з генеральної сукупності N виробів утворюють вибірку об’єму N.

Дискретними випадковими величинами називають такі, котрі можуть набувати лише певні значення, наприклад: 0,1; 0,2; 0,3 і т.д.

Безперервними випадковими величинами називають такі, котрі в деякому інтервалі можуть набувати будь-яке значення.

Число бракованих виробів в різноманітних вибірках з генеральної сукупності є дискретна випадкова величина, а розмір цих виробів – безперервна випадкова величина.

Дискретна випадкова величина задана, якщо є ймовірність кожного її значення (табл. 1).

Таблиця 1

X	X1	x2	x3	…	xn
P(X=xi)	P(x1)	P(x2)	P(x3)	…	P(xn)

Будь-яку безперервну випадкову величину можна задати у вигляді дискретної, якщо всі можливі її значення розбити на інтервали і задати ймовірність появи цих інтервалів (через обмеженість вимірювальних засобів всі заміри безперервних величин задаються в дискретному вигляді).

Дамо поняття щільності та інтегральної функції розподілу випадкових величин.

Якщо Х – випадкова величина, а х – деяке її значення, то ймовірність того, що Х < х рівна:

F(x) =P(X< x),(1),

де F(х) – так звана інтегральна функція розподілу (рис. 1). На рис. 1 F(x) – ордината кривої в деякій точці х. При будь-якому х0 = F(x) = 1.

Густина ймовірності φ(х) є границя відношення ймовірності того, що випадкова величина Х набуде значення, котре лежить між х і х + Δх, до величини інтервалу Δх при Δх→0, тобто:

. (2)

Функцію φ(х) називають також диференційним законом розподілу.

φ(х) і F(x) зв’язані співвідношенням:

<< Х < х). (2а)

Будемо вважати, що випадкова величина задана теоретичним законом, якщо задані її інтегральний закон або густина ймовірності.

Випадкова величина задана емпіричним законом розподілу, якщо для кожного значення випадкової величини відомі частота, з якою вона зустрічається, або частість отримання з N дослідів (табл. 2).

Рис. 1

Таблиця 2

Значення х	х1	х2	х3	...	xn
Частоти	m1	m2	m3	...	mn
Частість				...

При

В границі частості прямують до ймовірностей відповідних значень випадкової величини.

Будь-який теоретичний розподіл характеризується величиною своїх основних параметрів: математичним очікуванням МХ (центром групування) і дисперсією DX (величиною розсіювання).

Для дискретної випадкової величини (див. табл. 1).

; (3)

; (4)

; (5)

;(6)

Або ; (7)

; (8)

Рис. 2

Формули (5), (6) застосовуються для тих випадків, коли випадкова величина приймає значення від a до b; формули (7), (8) – коли Х змінюється від – ∞ до ∞.

називається середнім квадратичним відхиленням або стандартом.

Емпіричний розподіл характеризується середнім значенням , рівним:

. (9)

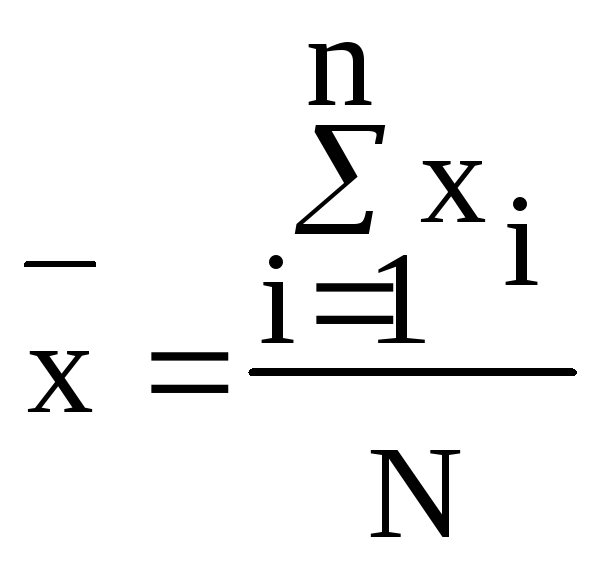
або . (9а)

Середнє значення характеризує центр групування значень випадкової величини. При достатньо великому N – (N → ∞)вибіркове значення х по величині прямує до математичного очікування, тобто х ≈ МХ.

Величина розсіювання вибіркових значень навколо їх середнього значення характеризується емпіричною дисперсією S² , дорівнює:

. (10)

Для N ≥ 25замість формули (10) користуються формулою (10а):

, (10а)

де .

називається емпіричним середнім квадратичним відхиленням.

При N → ∞ S² ≈ DX .

Крім середнього значення і дисперсії, криві розподілення характеризуються також асиметрією (А) і ексцесом (Е):

. (11)

Якщо А = 0 , то крива – симетрична. Якщо А > 0 – крива має позитивну асиметрію, а якщо А < 0 – негативну (рис. 3).

А = 0 А > 0 А < 0

Рис. 3

Ексцес характеризує крутизну кривої. За кривоу з нульовим ексцесом прийнята крива нормального розподілення, що має густину ймовірності:

(12)

де α = МХ – математичне очікування;

σ² – дисперсія.

Якщо Е > 0 , то говорять, що маємо позитивний ексцес, тобто вершина кривої знаходиться вище кривої нормального розподілу. Якщо Е < 0 – маємо негативний ексцес, і вершина кривої знаходиться нижче кривої нормального розподілу (рис. 4).

Нормальна Нормальна

φ(х) крива φ(х) крива

0 х 0 х

Е < 0 Е > 0

Рис. 4

У багатьох технічних додатках [*], [**], [***] функції розподілу характеризуються коефіцієнтом відносного розсіювання (К), коефіцієнтом відносної асиметрії (α) і величиною практично граничного поля розсіювання. Дамо визначення цих понять.

Будемо вважати, що похибка відхилень розмірів від їх номінального значення задана функцією густини φ(х) і величинами параметрів МХ, DX (рис. 5). Приймемо номінальне значення за початок координат.

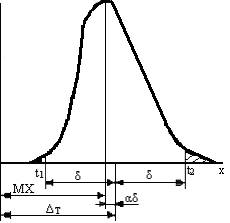
Рис. 5

Практично граничним полем розсіювання називають відстань між такими двома значеннями t₁ i t₂ випадкової величини, при яких площа, обмежена кривою, віссю абсцис і відрізком [t₁, t₂], дорівнює 1 – 2β, де 2β – ймовірність ризику (браку). Зазвичай приймають 2β = 0,0027. За визначенням можна написати

__________________

* Бородачев Н.А. Анализ качества и точности производства, М., Машгиз, 1960.

** Бородачев Н.А. Основные вопросы теории точности производства. Академиздат, 1950.

*** Вандер Ваден Б.А. Математическая статистика, М. ИЛ., 1960.

На практиці звичайно t₁ i t₂вибирають так, що

.

Визначене таким чином практично граничне поле розсіювання приймають за поле допуску, тобто 2δ_т = t₂-t₁.

Введемо позначення:

– половина поля допуску;

– координата середини поля допуску (рис. 5);

– коефіцієнт відносної асиметрії;

–коефіцієнт відносного розсіювання, де .

(індекс „Т” при Δ, δ, α, К вказує на теоретичне значення цих коефіцієнтів. Ці ж коефіцієнти, що визначаються для емпіричних розподілень, будуть мати в подальшому індекс „Э” і позначатися Δ_э, δ_э, α_э, К_э).

В тих випадках, коли метою експерименту є лише визначення і уточнення коефіцієнтів відносно заданого конструктором поля допуску, що не підлягає перегляду, коефіцієнти α_э і К_э визначаються за формулами:

.

При цьому може виявитись, що задане конструктором поле допуску не відповідає практично граничному полю розсіювання, тобто ймовірність ризику (браку) не дорівнює 2β = 0,0027.

Практично граничне поле розсіювання виявляється нерівним полю допуску також у тих випадках, коли за величину поля допуску приймається вся зона розсіювання R (величина розмаху), рівна різниці між максимальним і мінімальним значеннями випадкової величини в вибірці, тобто R = x_max – x_min .