
- •Ю.П.Золотухин, а.А.Гринь Практикум по дифференциальной геометрии
- •Часть 1
- •Часть 1.
- •Содержание
- •Предисловие
- •Введение
- •§1. Вектор-функции
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •Часть I. Кривые на плоскости и в пространстве
- •§2. Способы задания кривых
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§3. Замечательные кривые
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§4. Касательная прямая. Длина дуги. Натуральная параметризация
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§5. Сопровождающий трехгранник. Кривизна и кручение
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§6. Формулы Френе. Натуральные уравнения. Эволюта и эвольвента
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§7. Плоские кривые
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§8. Дополнительные задачи
- •Группа в
- •1. Плоские алгебраические кривые третьего порядка
- •Литература а. Основные учебники
- •Б. Дополнительная литература учебного характера
- •В. Сборники задач
- •Г. Методические указания
- •Д. Литература справочно-энциклопедического характера
- •Е. Вводные курсы, научно-популярная литература
- •Ж. Литература по истории дифференциальной геометрии
Упражнения и задачи для самостоятельной работы
Группа А
Написать уравнения ребер и граней сопровождающего трехгранника кривой
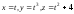 в точке (1;1;5).
в точке (1;1;5).
Найти точки на кривой
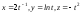 ,
в которых ее бинормаль параллельна
плоскостиxy+8z+2=0.
,
в которых ее бинормаль параллельна
плоскостиxy+8z+2=0.
Найти точку, в которой кривизна кардиоиды
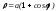
принимает наименьшее значение, и найти это значение.
Есть ли на кардиоиде точки спрямления?
Показать, что кривая
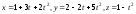 плоская, и найти уравнение плоскости,
в которой она расположена.
плоская, и найти уравнение плоскости,
в которой она расположена.
5.
Показать, что кривизна регулярной
плоской кривой, заданной полярным
уравнением
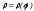 ,
может быть вычислена по формуле
,
может быть вычислена по формуле
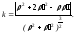
Группа Б
На бинормалях винтовой линии отложены единичные отрезки. Какую кривую образуют концы этих отрезков?
Доказать, что если все соприкасающиеся плоскости проходят через одну и ту же точку, то кривая плоская.
Доказать, что кривизна гладкой кривой F(x,y)=0 может быть вычислена по формуле:
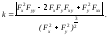
Найти кривизну кривых, заданных дифференциальным уравнением P(x;y)dx+Q(x;y)dy = 0.
10.
На кривой
 найти
точки спрямления, точки уплощения и
дуги, на которых кручение сохраняет
знак.
найти
точки спрямления, точки уплощения и
дуги, на которых кручение сохраняет
знак.
§6. Формулы Френе. Натуральные уравнения. Эволюта и эвольвента
Основные вопросы
Репер Френе (канонический репер). Формулы Френе.
Натуральные уравнения кривой.
Эволюта плоской кривой.
Эвольвента кривой.
Упражнения с решениями
1.
Пусть
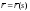 -
натуральная параметризация пространственной
кривой,
-
натуральная параметризация пространственной
кривой,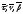 -
векторы ее репера Френе. Доказать
тождества: а)
-
векторы ее репера Френе. Доказать
тождества: а)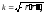 б)
б)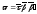 .
.
Доказательство. а) Используя формулы Френе, имеем:
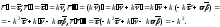
б) Применяя третью формулу Френе, получаем:
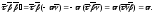
Составить натуральные уравнения кривой
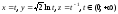 .
.
Решение. Найдем зависимость между параметром t и натуральным параметром s. Имеем:
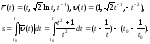
Полагая
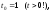 получаем,
что
получаем,
что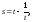 откуда находим зависимость s от t:
откуда находим зависимость s от t:
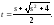
Вычисляя теперь
кривизну и кручение данной кривой как
функции параметра t
и учитывая найденную зависимость,
находим натуральные уравнения: 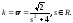
(Здесь учтено, что
множество значений функции
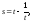 t>0
- вся числовая прямая).
t>0
- вся числовая прямая).
Ответ:
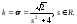
Найти параметрические уравнения плоской кривой, зная ее натуральные уравнения:
а)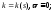 б)
б)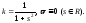
Решение.
а) Пусть x
= x(s),
y
= y(s)
- натуральная параметризация кривой,
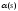 -
угол, образованный касательной к этой
кривой в точке с параметромs
и осью х.
Орт касательной имеет тогда вид:
-
угол, образованный касательной к этой
кривой в точке с параметромs
и осью х.
Орт касательной имеет тогда вид: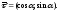 Следовательно,
Следовательно,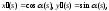 и
и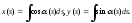
Кроме того,
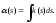
В
самом деле, дифференцируя соотношение
 и пользуясь формулами Френе, получим:
и пользуясь формулами Френе, получим:
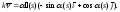
Отсюда
вытекает соотношение
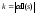 ,
которое удобнее заменить соотношением
,
которое удобнее заменить соотношением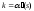 ,
присваивая кривизне соответствующий
знак.
,
присваивая кривизне соответствующий
знак.
б) В соответствии с результатами, полученными в пункте а), находим:
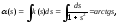
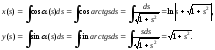
(здесь взяты конкретные значения констант интегрирования, поскольку они влияют только на положение кривой на плоскости, но не на ее форму).
Итак, найдена натуральная параметризация кривой, заданной натуральными уравнениями:
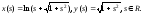
Исключая из этих соотношений параметр s, получаем: y = chx.
Ответ:
а)
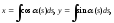 где
где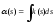 ;
;
б)
 ( цепная линия ).
( цепная линия ).
Найти уравнение эволюты регулярной плоской кривой
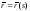 (s
- натуральный параметр). Показать, что
расстояние между соответствующими
точками плоской кривой и ее эволюты
равно радиусу кривизны кривой. ( Эволютой
плоской
кривой называется кривая, каждая
касательная которой служит нормалью
этой кривой.)
(s
- натуральный параметр). Показать, что
расстояние между соответствующими
точками плоской кривой и ее эволюты
равно радиусу кривизны кривой. ( Эволютой
плоской
кривой называется кривая, каждая
касательная которой служит нормалью
этой кривой.)
Решение.
Будем искать уравнение эволюты в виде:
 где
где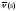 -
орт нормали кривой
-
орт нормали кривой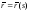 .
В силу определения эволюты направляющий
вектор
.
В силу определения эволюты направляющий
вектор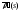 ее
касательной коллинеарен вектору
ее
касательной коллинеарен вектору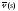 .
.
Применяя формулы Френе, его можно записать так:

Следовательно,
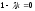 ,
т.е.
,
т.е.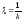 .
Итак, уравнение эволюты имеет вид
.
Итак, уравнение эволюты имеет вид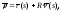 где
где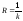 - радиус кривизны кривой. Очевидно,
- радиус кривизны кривой. Очевидно,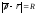 .
.
Ответ:
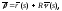 где
где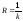 (k
- кривизна кривой).
(k
- кривизна кривой).
Замечание1. Здесь, кроме того, показано, что эволюта - геометрическое место центров кривизны кривой.
Замечание2.
Эволюта плоской кривой
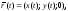 гдеt
- произвольный параметр, может быть
задана уравнением
гдеt
- произвольный параметр, может быть
задана уравнением
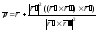
или в координатах:
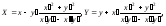

где
X,Y
- координаты радиус-вектора
 точки эволюты. (Эти уравнения могут быть
легко получены из следующих:
точки эволюты. (Эти уравнения могут быть
легко получены из следующих: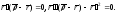 Первое непосредственно вытекает из
определения эволюты, второе получается
из него дифференцированием по параметруt.)
Первое непосредственно вытекает из
определения эволюты, второе получается
из него дифференцированием по параметруt.)
Найти уравнение эвольвенты регулярной кривой
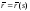 (s
- натуральный параметр). (Эвольвентой
или разверткой
кривой называется ортогональная
траектория ее касательных, т.е. кривая,
пересекающая каждую касательную под
прямым углом).
(s
- натуральный параметр). (Эвольвентой
или разверткой
кривой называется ортогональная
траектория ее касательных, т.е. кривая,
пересекающая каждую касательную под
прямым углом).
Решение.
Пусть
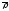 -
радиус-вектор текущей точки эвольвенты.
Тогда
-
радиус-вектор текущей точки эвольвенты.
Тогда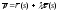 ,
где
,
где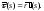 Чтобы найти
Чтобы найти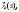 воспользуемся
ортогональностью
воспользуемся
ортогональностью и
и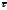 .
Применяя формулы Френе, имеем:
.
Применяя формулы Френе, имеем:
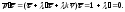
Таким
образом,
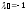 ,
т.е.
,
т.е.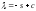 (с=const),
и
(с=const),
и
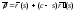 .
.
Ответ:
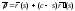 ,
где с - произвольная константа.
,
где с - произвольная константа.
Замечание3.
Эвольвенты кривой
 ,
гдеt
- произвольный параметр, очевидно, могут
быть заданы уравнением
,
гдеt
- произвольный параметр, очевидно, могут
быть заданы уравнением

или в координатах:
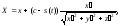

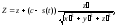
где
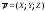 -
радиус-вектор точки эвольвенты,
-
радиус-вектор точки эвольвенты,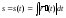 -
зависимость натурального параметра
данной кривой от параметраt,
с - произвольная постоянная.
-
зависимость натурального параметра
данной кривой от параметраt,
с - произвольная постоянная.
