
- •Ю.П.Золотухин, а.А.Гринь Практикум по дифференциальной геометрии
- •Часть 1
- •Часть 1.
- •Содержание
- •Предисловие
- •Введение
- •§1. Вектор-функции
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •Часть I. Кривые на плоскости и в пространстве
- •§2. Способы задания кривых
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§3. Замечательные кривые
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§4. Касательная прямая. Длина дуги. Натуральная параметризация
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§5. Сопровождающий трехгранник. Кривизна и кручение
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§6. Формулы Френе. Натуральные уравнения. Эволюта и эвольвента
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§7. Плоские кривые
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§8. Дополнительные задачи
- •Группа в
- •1. Плоские алгебраические кривые третьего порядка
- •Литература а. Основные учебники
- •Б. Дополнительная литература учебного характера
- •В. Сборники задач
- •Г. Методические указания
- •Д. Литература справочно-энциклопедического характера
- •Е. Вводные курсы, научно-популярная литература
- •Ж. Литература по истории дифференциальной геометрии
Введение
§1. Вектор-функции
Основные вопросы
Вектор-функции одной и двух переменных. Координатные функции. Годограф вектор-функции одной переменной.
Предел и производные вектор-функций. Классы непрерывных и гладких вектор- функций.
Правила дифференцирования вектор-функций.
Упражнения с решениями
Найти годографы вектор-функций:
а)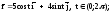
б)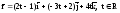 .
.
Решение. a) Выписывая координатные функции, получаем параметрические уравнения годографа:
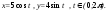
Исключая параметр t, имеем:
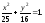
Учитывая
множества значений координатных функций
(Е(х)=[-5;5), E(y)=[-4;4]), заключаем, что годографом
вектор-функции
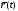 является эллипс
является эллипс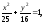 из которого исключена точка (5;0).
из которого исключена точка (5;0).
При
изменении t от 0 до
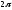 точка P(x;y)
на годографе движется по годографу от
точки (5;0) до этой же точки, совершая один
полный оборот против часовой стрелки.
точка P(x;y)
на годографе движется по годографу от
точки (5;0) до этой же точки, совершая один
полный оборот против часовой стрелки.
б) Параметрические уравнения годографа имеют вид
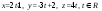 ,
,
и задают прямую в пространстве, проходящую через точку (-1; 2; 0) в направлении вектора ( 2; -3; 4). Ее канонические уравнения:
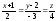 .
.
При
изменении t
от
 точка Р(x;
y;
z)
движется по годографу в направлении
вектора (2; -3; 4).
точка Р(x;
y;
z)
движется по годографу в направлении
вектора (2; -3; 4).
Ответ:
а) эллипс
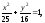 из которого исключена точка (5;0),
из которого исключена точка (5;0),
б) прямая
 .
.
Найти производные вектор-функций:
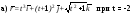 ;
;
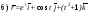 в точке (1;
1; 1).
в точке (1;
1; 1).
Решение. а) Имеем:
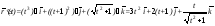 .
.
Подставляя вместо t значение -2, находим:
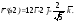
б)Определяем
значение параметра t,
соответствующее точке (1; 1; 1), решая
систему уравнений
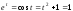 .Получаемt=0.
Далее вычисляем:
.Получаемt=0.
Далее вычисляем:
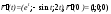 .
.
Ответ:
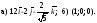
Найти
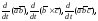
если
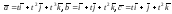 .
*
.
*
Решение. Вычисляя последовательно скалярное, векторное и смешанное произведения соответствующих векторов, находим:
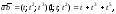
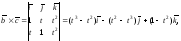
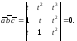
Дифференцируя полученные функции, окончательно имеем:
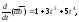
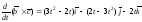 ,
,
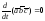 .
.
Ответ:
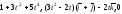 .
.
Пусть
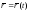 ,
где
,
где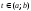 ,-вектор-функция
класса
,-вектор-функция
класса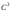 .
.
Найти производные следующих функций:
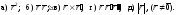
Решение.
a)
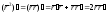 ;
;
б)
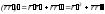 ;
;
в)
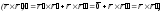
г)
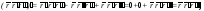
д)
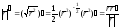 .
.
Ответ:
а)
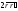 ;
б)
;
б)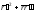 ;
в)
;
в)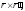 г)
г)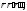 д)
д)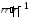 .
.
Для вектор-функции
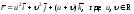 ,
,
найти:
а)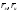 в
точке (1;0;-1); б)
в
точке (1;0;-1); б)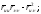
в)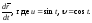 (Использованы обозначения:
(Использованы обозначения:
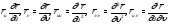 )
)
Решение. а) Находим частные производные вектор-функции
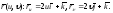 Определяем значения
параметров u,
Определяем значения
параметров u,
соответствующие точке (1;0;-1), решая систему уравнений:
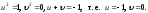 Окончательно
получаем:
Окончательно
получаем:
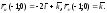
б)
Имеем:
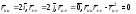 .
.
в)
Используя формулу
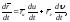 вычисляем:
вычисляем:
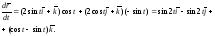
Ответ:
а)
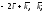 б) 0;
в)
б) 0;
в)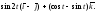
Упражнения и задачи для самостоятельной работы
Группа А
Найти годографы вектор-функций:
а)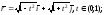
б)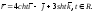
Найти производные вектор-функций:
а)
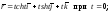
б)
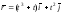 в точке (-2;1).
в точке (-2;1).
Найти
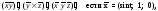
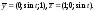
Пусть
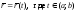 ,
-
вектор-функция
класса
,
-
вектор-функция
класса
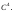
Найти производные следующих функций:
а)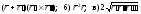
Для вектор-функции
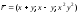 найти:
найти:
а)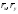 в точке (2;0;1);
б)
в точке (2;0;1);
б)
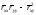 ;в)
;в)

Группа Б
Доказать, что траектория материальной точки, движущейся под действием центральной силы, является плоской. (Центральную силу можно представить в виде
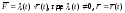 -
уравнение траектории движения)
-
уравнение траектории движения)
Пусть
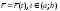 ,
- вектор-функция класса
,
- вектор-функция класса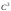 ,
а
,
а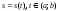 ,
-диффеоморфизм класса
,
-диффеоморфизм класса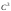 ,
осуществляющий замену аргумента.
Произвести замену аргумента в выражениях:
,
осуществляющий замену аргумента.
Произвести замену аргумента в выражениях: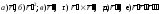
(штрихом обозначены производные по t).
Вектор-функция
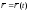 удовлетворяет дифференциальному
уравнению
удовлетворяет дифференциальному
уравнению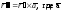 -постоянный
вектор. Доказать равенства: а)
-постоянный
вектор. Доказать равенства: а)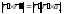 б)
б)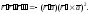
Пусть
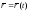 -
гладкая вектор-функция, и
-
гладкая вектор-функция, и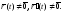
Доказать:
а)
для того, чтобы для любого t
векторы
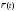 имели одинаковую длину, необходимо и
достаточно, чтобы векторы
имели одинаковую длину, необходимо и
достаточно, чтобы векторы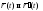 были
ортогональны;
были
ортогональны;
б)
для того, чтобы для любого t
векторы
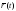 имели одинаковое направление, необходимо
и достаточно, чтобы векторы
имели одинаковое направление, необходимо
и достаточно, чтобы векторы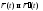 были
коллинеарны.
были
коллинеарны.
Пусть
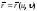 -
гладкая вектор-функция, и
-
гладкая вектор-функция, и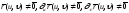 .
.
Доказать:
а)
для того, чтобы для любых u
и векторы
векторы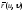 имели одинаковую длину, необходимо и
достаточно, чтобы вектор
имели одинаковую длину, необходимо и
достаточно, чтобы вектор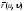 был ортогонален векторам
был ортогонален векторам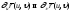 ;
;
б)
для того, чтобы для любых u
и векторы
векторы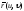 имели одинаковое направление, необходимо
и достаточно, чтобы векторы
имели одинаковое направление, необходимо
и достаточно, чтобы векторы
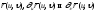 были
коллинеарны.
были
коллинеарны.
(Использованы
обозначения:
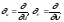 )
)
