- •Ю.П.Золотухин, а.А.Гринь Практикум по дифференциальной геометрии
- •Часть 1
- •Часть 1.
- •Содержание
- •Предисловие
- •Введение
- •§1. Вектор-функции
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •Часть I. Кривые на плоскости и в пространстве
- •§2. Способы задания кривых
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§3. Замечательные кривые
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§4. Касательная прямая. Длина дуги. Натуральная параметризация
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§5. Сопровождающий трехгранник. Кривизна и кручение
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§6. Формулы Френе. Натуральные уравнения. Эволюта и эвольвента
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§7. Плоские кривые
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§8. Дополнительные задачи
- •Группа в
- •1. Плоские алгебраические кривые третьего порядка
- •Литература а. Основные учебники
- •Б. Дополнительная литература учебного характера
- •В. Сборники задач
- •Г. Методические указания
- •Д. Литература справочно-энциклопедического характера
- •Е. Вводные курсы, научно-популярная литература
- •Ж. Литература по истории дифференциальной геометрии
Упражнения и задачи для самостоятельной работы
Группа А
Для каждой из заданных кривых составить уравнение касательной прямой, а также нормали (если кривая плоская) или нормальной плоскости (если кривая пространственная) в указанной точке; сделать рисунки кривых:
а) y=tgx (в точке с абсциссой 0);
б)
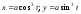 (в произвольной точке);
(в произвольной точке);
в)
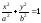 (в произвольной точке);
(в произвольной точке);
г)
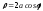 (в точке, для которой
(в точке, для которой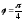 );
);
д)
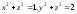 (в произвольной точке).
(в произвольной точке).
Найти точки пересечения и углы, под которыми пересекаются следующие кривые; сделать рисунки:
а)
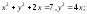 б)
б)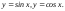
Вычислить:
а) длину дуги трактрисы между двумя ее произвольными точками;
б)
длину кардиоиды, заданной полярным
уравнением:
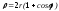 (см. рис.9);
(см. рис.9);
в)
длину дуги кривой
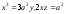 ,
заключенной между плоскостями
,
заключенной между плоскостями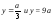 .
.
Найти натуральные параметризации кривых:
а)
окружности
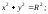 б)
винтовой линииx
= acost,
y
= asint,
z
= bt;
б)
винтовой линииx
= acost,
y
= asint,
z
= bt;
в) гиперболической винтовой линии x = acht, y = asht, z = at.
Траектория движения точки задана в цилиндрических координатах:
 ,
,
где
t - время,
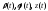 -
известные функции. Найти: а) косинус
угла
-
известные функции. Найти: а) косинус
угла между
радиус- вектором движущейся точки и
вектором ее мгновенной скорости; б)
длину дуги траектории между точками с
параметрами
между
радиус- вектором движущейся точки и
вектором ее мгновенной скорости; б)
длину дуги траектории между точками с
параметрами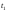 и
и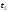 .
.
5.2 То же задание, если траектория движения точки задана в сферических координатах:
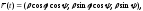 где t - время,
где t - время,
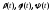 -
известные функции.
-
известные функции.
Группа Б
6.
Найти множество вершин прямых углов,
касающихся: а) параболы
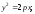 б)
эллипса
б)
эллипса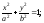 в)
гиперболы
в)
гиперболы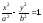
7.
Пусть касательная к гладкой кривой y
= y(x)
в точке М пересекает ось х
в точке Т, а нормаль - в точке N, и пусть
 -
проекция точки М на осьх.
Доказать, что длины касательной МТ,
нормали MN, подкасательной
-
проекция точки М на осьх.
Доказать, что длины касательной МТ,
нормали MN, подкасательной
 Т
и поднормали
Т
и поднормали N
выражаются формулами:
N
выражаются формулами:
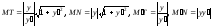
8.
Показать, что тангенс угла
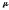 ,
образованного касательной к гладкой
кривой
,
образованного касательной к гладкой
кривой
с
радиус-вектором точки касания, может
быть найден по формуле
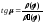 .
.
Используя
эту формулу, найти все кривые, пересекающие
под постоянным углом
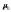 все лучи, выходящие из полюса.
все лучи, выходящие из полюса.
9.
Найти длину дуги одного витка кривой
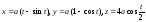 между двумя ее точками пересечения с
плоскостьюxz.
между двумя ее точками пересечения с
плоскостьюxz.
10.
Найти длину замкнутой кривой
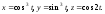
§5. Сопровождающий трехгранник. Кривизна и кручение
Основные вопросы
Сопровождающий трехгранник пространственной кривой. Касательная, бинормаль, главная нормаль. Соприкасающаяся, нормальная и спрямляющая плоскости.
Кривизна кривой. Точки спрямления.
Кручение кривой. Точки уплощения.
Упражнения с решениями
Найти уравнения ребер и граней сопровождающего трехгранника винтовой линии
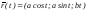 в произвольной точке, а также кривизну
в произвольной точке, а также кривизну и
кручение
и
кручение .
.
Решение. Последовательно находим:
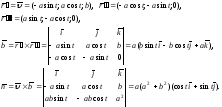
Следовательно, искомые уравнения имеют вид:
(1)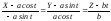 (касательная),
(касательная),
(2)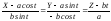 (бинормаль),
(бинормаль),
(3)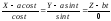 (главная нормаль),
(главная нормаль),
(4)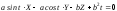 (нормальная
плоскость),
(нормальная
плоскость),
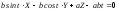 (соприкасающаяся
плоскость),
(соприкасающаяся
плоскость),
 (спрямляющая
плоскость).
(спрямляющая
плоскость).
Переходя к вычислению кривизны и кручения винтовой линии, имеем:
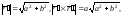
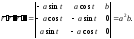
Следовательно,
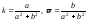 .
.
Ответ:
Уравнения
ребер - (1), (2), (3), уравнения граней - (4),
(5), (6). Кривизна -
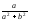 ,
кручение -
,
кручение -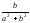 .
.
Найти уравнение соприкасающейся плоскости кривой
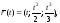 проходящей через точку М(0;0;9).
проходящей через точку М(0;0;9).
Решение. Находим нормальный вектор соприкасающейся плоскости данной кривой в ее точке с параметром t:
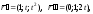
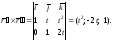
Уравнение
соприкасающейся плоскости, проходящей
через точку
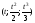 и
перпендикулярной вектору
и
перпендикулярной вектору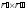 ,
можно записать в виде:
,
можно записать в виде:
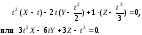
Подставляя координаты точки М в полученное уравнение, находим значение параметра t, при котором соприкасающаяся плоскость проходит через эту точку: t = 3. Таким образом, искомое уравнение имеет вид: 9X-6Y+Z-9 = 0.
Ответ: 9X-6Y+Z-9 = 0.
Найти вершины указанных кривых, т.е. точки, в которых их кривизна принимает экстремальные значения, а также найти эти значения: а)
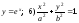
Есть ли на этих кривых точки спрямления?
Решение.
а) Имеем:
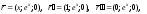
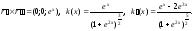
Исследование
показывает, что функция k=k(x),
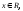 имеет единственную точку экстремума:
имеет единственную точку экстремума: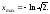 В точке
В точке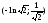 кривизна принимает максимальное
значение:
кривизна принимает максимальное
значение: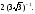 При
При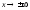 кривизна стремится к нулю. Точек
спрямления нет, так как
кривизна стремится к нулю. Точек
спрямления нет, так как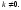
б)
Параметризуем эллипс:
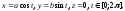
Вычисляя
кривизну, находим:
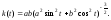
Функция
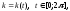 достигает экстремальных значений в тех
точках, в которых имеет экстремальные
значения функция
достигает экстремальных значений в тех
точках, в которых имеет экстремальные
значения функция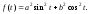 Исследование показывает, что таковыми
являются точки
Исследование показывает, что таковыми
являются точки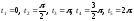 На эллипсе им соответствуют точки (a;0),
(0;b),
(-a;0),
(0;-b).
Кривизна принимает в них значения
На эллипсе им соответствуют точки (a;0),
(0;b),
(-a;0),
(0;-b).
Кривизна принимает в них значения
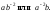 Точки спрямления отсутствуют, так как
Точки спрямления отсутствуют, так как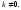
Ответ:
а) Максимальное значение кривизны -
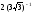 (
в точке
(
в точке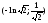 ),
точек спрямления нет; б) Кривизна
достигает экстремальных значений (
),
точек спрямления нет; б) Кривизна
достигает экстремальных значений (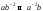 )
в вершинах эллипса. Точек спрямления
нет.
)
в вершинах эллипса. Точек спрямления
нет.
Показать, что кривая, образованная пересечением цилиндров
 является плоской, и найти уравнение
плоскости, в которой она расположена.
является плоской, и найти уравнение
плоскости, в которой она расположена.
Решение.
Параметризуем кривую:
 Вычислим ее кручение
Вычислим ее кручение .
.
Имеем:
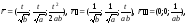
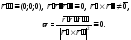
Последнее тождество означает, что данная кривая - плоская.
Подставляя,
например, значения
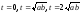 в параметрические уравнения кривой,
находим три точки, ей принадлежащие:
в параметрические уравнения кривой,
находим три точки, ей принадлежащие: Уравнение плоскости, проходящей через
эти точки, имеет вид:
Уравнение плоскости, проходящей через
эти точки, имеет вид: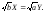
Ответ:
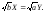
5.
Показать, что кривизна регулярной
плоской кривой, заданной параметрическими
уравнениями x
= x(t),
y
= y(t),
может быть вычислена по формуле
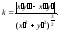
Решение.
Имеем:
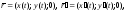
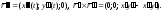
Итак,