2. Часть I. Кривые на плоскости и в пространстве

   1. §2. Способы задания кривых

      1. Основные вопросы

1. Параметризованные кривые. Параметризация кривой в декартовых координатах.

2. Регулярные кривые.

3. Замена параметра. Эквивалентные параметризации.

4. Явное и неявное задания кривых в декартовых координатах.

5. Задание кривых в недекартовых координатах.

1. Упражнения с решениями

1. Составить параметрические уравнения луча

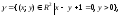
принимая в качестве параметра: а) абсциссу х точки луча;

б) расстояние s от точки луча до его вершины.

Решение: а)Пусть M(x;y) - произвольная точка луча .

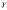Полагая x = t (t >-1), находим из уравнения луча: y = t+1. Соответствующие параметрические уравнения луча имеют вид:;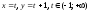

б) Из прямоугольного треугольника LMN где L - начало луча, N - проекция точки M на ось х, полагая ML=s ( s >0 ), получим:

LN=MN=s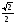. Учитывая, что ON=LN-1= s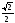-1, составляем параметрические уравнения луча :.

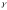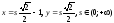Ответ: а) 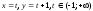; б).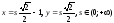

2. Показать, что вектор-функци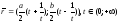и и

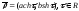, заданные в декартовых координатах, определяют эквивалентные регулярные параметризации кривой. Указать эту кривую. (Здесь и далее, если не оговаривается другого, параметры а, b считаются положительными.)

Решение. Будем искать взаимно-обратные замены параметров, удовлетворяющие соотношению

.

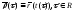Имеем:

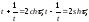
откуда 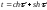, или, что то же самое ,.

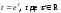Найденная функция является диффеоморфизмом класса 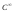прямойR на луч 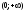. Обратный диффеоморфизм есть функция.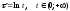

Итак, параметризации 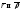- эквивалентные параметризации класса.

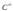Проверим, что параметризация 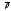- регулярная: она принадлежит классу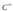, и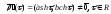. Следовательно, и параметризацияявляется регулярной (класса).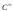

Чтобы определить форму кривой, воспользуемся параметрическими уравнениями .

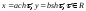Исключая параметр , получаем: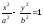. Учитывая, что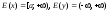, приходим к выводу, что данная кривая - правая ветвь гиперболы.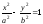

Ответ: Правая ветвь гиперболы .

3. Записать параметрические уравнения плоской кривой, заданной уравнением 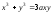(декартов лист; см.рис.1), принимая в качестве параметра точки кривой отношение t ее ординаты к абсциссе. Указать порядок точек на кривой, определяемый полученной параметризацией. Найти особые точки неявного задания декартового листа.

Решение. Заменяя в данном уравнении y по формуле y=tx, выражаем абсциссу x, а затем ординату y текущей точки кривой через параметр t:

.

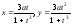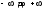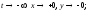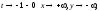Для определения порядка точек, изменяя параметр t от , находим контрольные и предельные точки кривой. В частности, имеем: приприпри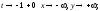приt=0 x=y=0;

при

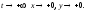
(В других случаях может возникнуть необходимость в более детальном исследовании поведения функций x=x(t) и y=y(t).)

Анализируя полученные результаты, приходим к выводу: полученная параметризация отвечает разбиению декартова листа на две непересекающиеся элементарные кривые (можно показать, что они являются регулярными.) Одна из них, соответствующая изменению параметра t от 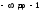, расположена строго внутриIV-го квадранта, причем точка на кривой движется в направлении от точки (0;0) вниз вправо. Другая из указанных элементарных кривых расположена во II-м и I-м квадрантах. При изменении t от точка движется в направлении от бесконечно удаленной точки кривой к точке (0;0), которую проходит приt=0, а далее огибает петлю, расположенную в I-м квадранте в направлении против часовой стрелки и подходит вплотную опять к точке (0;0).

Записывая неявное уравнение декартового листа в виде F(x,y)=0, где 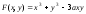, имеем: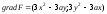. Нетрудно проверить, чтоgradF обращается в нуль-вектор только в точках (0;0) и (a;a), которые и являются особыми точками неявного задания этой кривой.

Ответ: .

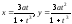
(0;0), (a;a) - особые точки неявного задания.

4. Параметризовать в декартовых координатах кривую, являющуюся линией пересечения сферы радиуса R и кругового цилиндра радиуса , одна из образующих которого проходит через центр сферы (Эта кривая называетсякривой Вивиани (см.рис.19).)

Решение. Выбирая прямоугольную декартову систему координат соответствующим образом, уравнение кривой Вивиани запишем в виде:

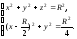
Полагая теперь 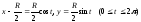, имеем:

.

Кривая Вивиани является общей кривой, состоящей из двух простых кривых-«петель», выходящих из одной точки. Полученные уравнения суть параметризации каждой из этих петель в отдельности (верхней соответствует знак плюс, нижней - минус). Нетрудно записать уравнения, задающие единую параметризацию данной кривой.

Ответ: .

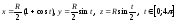4. Кривая задана уравнением в полярных координатах. Записать:

а) ее параметрические уравнения в декартовых координатах; б) ее уравнение в декартовых координатах.(Здесь и далее, если не оговаривается другое, считать, что полярная ось совпадает с неотрицательной полуосью абсцисс.)

Решение: а) Вводя в качестве параметра полярный угол 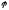точки кривой и используя формулы, выражающие связь между ее декартовыми (x;y) и полярными 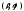координатами, имеем: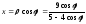

.

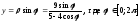б) Перепишем данное уравнение в эквивалентной форме: .

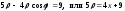Обе части полученного уравнения неотрицательны, поэтому, возведя его в квадрат и используя равенство 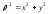, получим равносильное уравнение: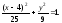

(Данная кривая-эллипс с центром в точке (4;0) и полуосями 5 и 3.)

Ответ: а),;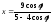

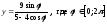б)