3. Упражнения и задачи для самостоятельной работы

Группа А

1. Составить параметрические уравнения луча

принимая в качестве параметра: а) ординату y точки луча; б) угол 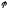между осьюx и радиус-вектором точки луча.

2. Показать, что вектор-функции

и

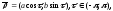
заданные в декартовых координатах, являются эквивалентными регулярными параметризациями кривой. Указать эту кривую.

3. Записать параметрические уравнения плоской кривой, заданной уравнением

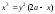(циссоида Диоклесса; см.рис.2), принимая в качестве параметра точки кривой отношение t ее ординаты к абсциссе. Указать порядок точек на кривой, определяемый полученной параметризацией. Найти особые точки неявного задания циссоиды.

3. Параметризовать в декартовых координатах кривую, являющуюся линией пересечения двух прямых круговых цилиндров радиусов а и b , оси которых пересекаются под прямым углом (Эта кривая называется бицилиндрикой (см. рис. 20)). Показать, что каждая из двух компонент бицилиндрики является простой регулярной кривой.

Указание. Оси х,у прямоугольной декартовой системы координат в пространстве совместить с осями цилиндров.

1. Кривая задана уравнением в полярных координатах. Записать: а) ее параметрические уравнения в декартовых координатах;б) ее уравнение в декартовых координатах.

2. То же задание для кривой заданной полярным уравнением

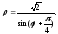
Группа Б

6. Параметризовать полуокружность ,

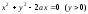приняв в качестве параметра:

а) угловой коэффициент k прямой, проходящей через начало координат и точку окружности;

б) угол 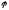между осьюx и прямой, проходящей через точку окружности и ее центр, отсчитываемый от оси x против часовой стрелки.

Будут ли эти параметризации регулярными? Эквивалентными?

6. Составить параметрические уравнения следующих кривых, принимая в качестве параметра угол t между осью х и радиус-вектором точки кривой:

а) эллипса 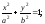б) гиперболы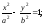в) параболы

6. Исключив параметр t, найти уравнения кривых в декартовых координатах и построить эти кривые:

а) ;

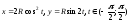б)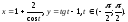

6. Составить параметрические уравнения диаметра сферы

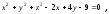перпендикулярного плоскости

1. Установить, какие кривые определяются следующими уравнениями

а) 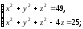б)

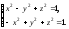
2. Показать, что кривая 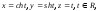лежит на гиперболическом цилиндре. Найти ее проекции на координатные плоскости.

1. §3. Замечательные кривые

   1. Основные вопросы

1. Плоские алгебраические кривые.

2. Плоские трансцендентные кривые.

3. Пространственные кривые.

1. Упражнения с решениями

1. Отрезок АВ длины а скользит своими концами по осям прямоугольной системы координат. Прямые АС и ВС, параллельные координатным осям, пересекаются в точке С, из которой проведен перпендикуляр СМ к прямой АВ. Написать уравнение кривой, являющейся траекторией точки М ( астроида (см.рис.4)).

Решение. Предположим, что точка А расположена на оси х, В - на оси у. Пусть далее М(x;y) - произвольная точка данной кривой. Выберем в качестве параметра t, определяющего положение точки М на кривой, угол ОАМ. Наша задача - выразить х и у через t.

Из треугольника АВС находим: 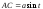, а из треугольника АМС -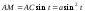. Далее рассматриваем треугольник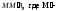проекция точки М на осьх. Имеем:

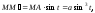
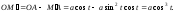
Итак, параметрические уравнения астроиды имеют вид:

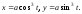
Исключая параметр t, получаем неявное уравнение астроиды в декартовых координатах: .

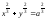Ответ: 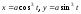(параметрические уравнения);

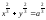(неявное уравнение в декартовых координатах).

2. Написать уравнение плоской кривой, состоящей из точек, произведение расстояний от которых до двух данных точек 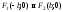есть величина постоянная, равная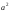(овалы Кассини, при а=b - лемниската Бернулли (см. рис. 5 и 6)).

Решение. Пусть М(x;y)-произвольная точка данной кривой. Тогда по определению имеем: 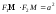, или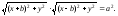

Упрощая это уравнение, получаем неявное уравнение овалов Кассини в декартовых координатах:

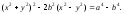
Переходя к полярным координатам, полученное уравнение перепишем в виде:

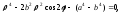
или

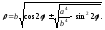
Если а > b, то овал имеет форму замкнутой кривой, симметричной относительно осей координат.

Если a < b, то имеем две замкнутые кривые.

При a = b получаем лемнискату Бернулли, неявное и полярное уравнения которой имеют соответственно вид:

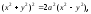
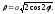
Ответ: 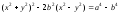(неявное уравнение в декартовых координатах),

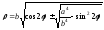(полярное уравнение).

2. Точка М равномерно движется по лучу ON, который равномерно вращается в плоскости вокруг начала О. Найти уравнение кривой, являющейся траекторией точки М (спираль Архимеда (см. рис.13)).

Решение. Примем точку О за полюс полярной системы координат, а начальное положение луча ON - за полярную ось. Будем считать, что в момент времени t = 0 точка М находилась в полюсе. Обозначим полярные координаты точки М через.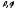

За время t луч ON повернулся на угол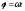, а точка М прошла по нему путь длины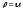, где- угловая скорость вращения луча,- линейная скорость движения точки М по лучуON (их следует считать известными величинами). Итак, полярное уравнение спирали Архимеда имеет вид:

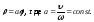
Ответ:

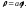
2. Окружность радиуса а катится по прямой l без скольжения. Найти уравнение кривой, являющейся траекторией точки М, жестко закрепленной на окружности (циклоида (см. рис. 15)).

Решение. В качестве оси х прямоугольной декартовой системы координат примем прямую l. Предположим, что в начальный момент движения точка М находилась в начале координат. Координаты точки М после поворота окружности на угол t будут равны: x=OS=OP-SP, y=SM=CP-CN, где С - центр окружности, Р - точка касания окружности и прямой l, S - проекция точки М на прямую l, N - проекция точки М на прямую СР.

Поскольку 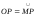=at, SP=MN=asint, CN=acost, то параметрические уравнения циклоиды имеют вид:

x=atasint, y=aacost.

Ответ: x=atasint, y=aacost.

2. Точка М движется по цилиндру 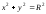так, что ее проекция на осьz перемещается с постоянной скоростью , а проекция на плоскостьху равномерно вращается по окружности с угловой скоростью . Найти уравнение кривой, являющейся траекторией точки М (винтовая линия (см. рис.21)).

Решение. Пусть в начальный момент времени точка М находится на оси х (совпадает с точкой А). Найдем координаты точки М в момент времени t. Обозначая через N проекцию точки M на плоскость ху, через P и Q ее проекции на оси х и у соответственно, находим:

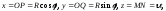
где 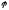-угол между векторами.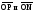

Учитывая, что 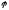=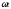, записываем параметрические уравнения винтовой линии:

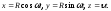
Ответ: