
- •Ю.П.Золотухин, а.А.Гринь Практикум по дифференциальной геометрии
- •Часть 1
- •Часть 1.
- •Содержание
- •Предисловие
- •Введение
- •§1. Вектор-функции
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •Часть I. Кривые на плоскости и в пространстве
- •§2. Способы задания кривых
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§3. Замечательные кривые
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§4. Касательная прямая. Длина дуги. Натуральная параметризация
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§5. Сопровождающий трехгранник. Кривизна и кручение
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§6. Формулы Френе. Натуральные уравнения. Эволюта и эвольвента
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§7. Плоские кривые
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§8. Дополнительные задачи
- •Группа в
- •1. Плоские алгебраические кривые третьего порядка
- •Литература а. Основные учебники
- •Б. Дополнительная литература учебного характера
- •В. Сборники задач
- •Г. Методические указания
- •Д. Литература справочно-энциклопедического характера
- •Е. Вводные курсы, научно-популярная литература
- •Ж. Литература по истории дифференциальной геометрии
§4. Касательная прямая. Длина дуги. Натуральная параметризация
Основные вопросы
Касательная прямая. Нормаль плоской кривой, нормальная плоскость пространственной кривой.
Угол между кривыми в точке их пересечения.
Длина дуги кривой. Натуральная параметризация.
Упражнения с решениями
Для каждой из заданных кривых составить уравнение касательной прямой, а также нормали (если кривая плоская) или нормальной плоскости (если кривая пространственная) в указанной точке; сделать рисунки кривых:
а)
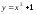 (в точке с абсциссой 0);
(в точке с абсциссой 0);
б)
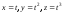 (в точке (2;4;8));
(в точке (2;4;8));
в)
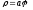 (в
точке, для которой
(в
точке, для которой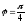 );
);
г)
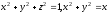 (в точке (0;0;1)).
(в точке (0;0;1)).
Решение.
а)Параметризуем кривую:
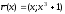 .
Находим координаты заданной точки (х=0,
y=1)
и вычисляем в ней вектор скорости
параметризации:
.
Находим координаты заданной точки (х=0,
y=1)
и вычисляем в ней вектор скорости
параметризации:
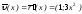 ,
,
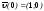 .
Следовательно, искомая касательная
имеет уравнение
.
Следовательно, искомая касательная
имеет уравнение
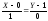 ,
илиY=1.
,
илиY=1.
Нормаль в заданной точке, очевидно, совпадает с осью y.
б) Параметр указанной точки находим, решая систему уравнений:
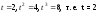 .
Имеем:
.
Имеем: .
.
Итак,
уравнение касательной прямой имеет
вид: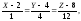
а уравнение нормальной плоскости -
(X-2)+4(Y-4)+12(Z-8)=0, или X+4Y+12Z-114=0.
в)
Параметризуем кривую, выбирая в качестве
параметра полярный угол
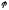 :
: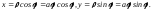 Находим
декартовы координаты точки
Находим
декартовы координаты точки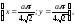 вектор скорости параметризации в ней:
вектор скорости параметризации в ней: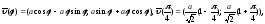
а также уравнение касательной -

и, наконец, уравнение нормали -
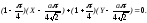
г)
Обозначим:
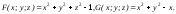 Находим:
Находим:
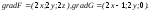 В
точке
(0;0;1)
имеем:
В
точке
(0;0;1)
имеем:
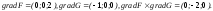 Следовательно,
уравнения касательной прямой и нормальной
плоскости соответственно имеют вид:
Следовательно,
уравнения касательной прямой и нормальной
плоскости соответственно имеют вид:
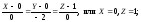
0(X-0)-2(Y-0)+0(Z-1)=0, или Y=0.
Ответ:
а) Y=1
и X=0;
б)
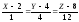 и X+4Y+12Z-114=0;
и X+4Y+12Z-114=0;
в)
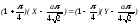 и
и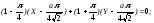
г) X=0, Z=1 и Y=0.
Доказать, что гиперболы
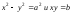 пересекаются под прямым углом .
пересекаются под прямым углом .
Доказательство.
Обозначим:
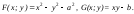
Имеем:
 Следовательно, в любой точке пересечения
гипербол
Следовательно, в любой точке пересечения
гипербол
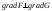 ,
т.е. их касательные прямые перпендикулярны.
,
т.е. их касательные прямые перпендикулярны.
Вычислить: а) длину дуги цепной линии
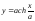 (см. рис.17) между точками с абсциссами
(см. рис.17) между точками с абсциссами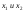 ;
б) длину одной арки циклоиды; в) длину
одного витка винтовой линии.
;
б) длину одной арки циклоиды; в) длину
одного витка винтовой линии.
Решение.
а) Параметризуя цепную линию
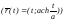 и
применяя формулу для нахождения длиныl
дуги параметризованной кривой
и
применяя формулу для нахождения длиныl
дуги параметризованной кривой
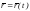 между точками с параметрами
между точками с параметрами , находим:
, находим:
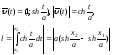
б) Параметрические уравнения циклоиды имеют вид (см. §3, п.II, задача 4):
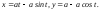
Одной
ее арке соответствует изменение параметра
t
от 0 до
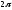 (см. рис.15). Поэтому имеем:
(см. рис.15). Поэтому имеем:
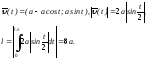
в) Параметрические уравнения винтовой линии имеют вид (см. §3, п.II, задача 5):
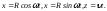
Одному
ее витку соответствует изменение
параметра t
от 0 до
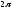 (см. рис.21). Поэтому имеем:
(см. рис.21). Поэтому имеем:
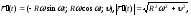
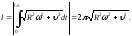
Ответ:
а)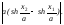 ;
б)8а; в)
;
б)8а; в)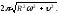
Найти натуральную параметризацию кривой
 .
.
Решение.
Воспользуемся формулой
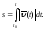
Положим
для простоты
 ,
т.е. отсчет длины дуги
,
т.е. отсчет длины дуги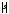 будем проводить от точки кривой, имеющей
параметрt=0.
Имеем:
будем проводить от точки кривой, имеющей
параметрt=0.
Имеем:
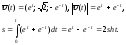
Решая
уравнение
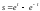 относительноt
получаем:
относительноt
получаем:
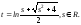
Следовательно, натуральная параметризация кривой имеет вид:
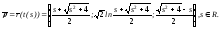
Ответ:
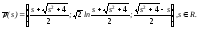
Вывести формулу для нахождения длины дуги плоской регулярной кривой, заданной полярным уравнением
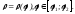 Используя эту формулу, найти длину
первого витка спирали Архимеда.
Используя эту формулу, найти длину
первого витка спирали Архимеда.
Решение.
Параметризуя кривую в виде
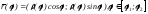 ,
и применяя формулу для нахождения длины
дуги параметризованной кривой
,
и применяя формулу для нахождения длины
дуги параметризованной кривой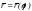 между точками с параметрами
между точками с параметрами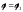 и
и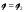 ,
получаем:
,
получаем:
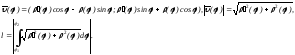
Найдем
длину первого витка спирали Архимеда
(см. §3,
п.II,
задача 3 и рис.13). Имеем:
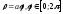 ,
,
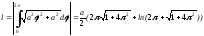 .
.
Ответ:
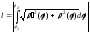 ,
,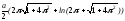 .
.
