
- •Ю.П.Золотухин, а.А.Гринь Практикум по дифференциальной геометрии
- •Часть 1
- •Часть 1.
- •Содержание
- •Предисловие
- •Введение
- •§1. Вектор-функции
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •Часть I. Кривые на плоскости и в пространстве
- •§2. Способы задания кривых
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§3. Замечательные кривые
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§4. Касательная прямая. Длина дуги. Натуральная параметризация
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§5. Сопровождающий трехгранник. Кривизна и кручение
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§6. Формулы Френе. Натуральные уравнения. Эволюта и эвольвента
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§7. Плоские кривые
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§8. Дополнительные задачи
- •Группа в
- •1. Плоские алгебраические кривые третьего порядка
- •Литература а. Основные учебники
- •Б. Дополнительная литература учебного характера
- •В. Сборники задач
- •Г. Методические указания
- •Д. Литература справочно-энциклопедического характера
- •Е. Вводные курсы, научно-популярная литература
- •Ж. Литература по истории дифференциальной геометрии
Упражнения и задачи для самостоятельной работы
Группа А
Пусть
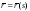 - натуральная параметризация
пространственной кривой класса
- натуральная параметризация
пространственной кривой класса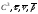 -
векторы ее репера Френе. Доказать
тождества:
-
векторы ее репера Френе. Доказать
тождества:
а)
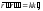 б)
б)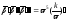
Составить натуральные уравнения кривой x = cht, y = sht, z = t,
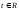 .
.
Найти параметрические уравнения плоской кривой, зная ее натуральные уравнения:
а)
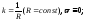 б)
б)
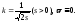
Найти уравнения и сделать чертежи эволют следующих плоских кривых: а)
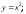
б)
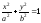 (рассмотреть случаи когда
(рассмотреть случаи когда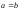 и
и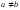 ).
).
Найти эвольвенты следующих кривых: а) цепной линии y = chx (проходящую через точку (0;1)); б) винтовой линии x = acost, y = asint, z = bt.
Группа Б
Доказать, что формулы Френе можно записать в виде:
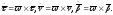 Найти вектор
Найти вектор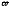 (вектор Дарбу).
(вектор Дарбу).
Обобщенной винтовой линией или линией откоса называется пространственная кривая, касательная к которой образует постоянный угол
 с фиксированным направлением. Для того,
чтобы бирегулярная кривая
с фиксированным направлением. Для того,
чтобы бирегулярная кривая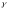 класса
класса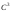 была
линией откоса необходимо и достаточно,
чтобы
была
линией откоса необходимо и достаточно,
чтобы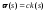 ,
где с=const.
Доказать.
,
где с=const.
Доказать.
Найти полярное уравнение кривой, заданной натуральными уравнениями
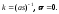
Доказать, что если вдоль регулярной кривой, не имеющей точек спрямления, производная кривизны по натуральному параметру сохраняет знак, то ее эволюта является регулярной кривой.
Выразить кривизну
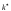 эвольвенты
регулярной кривой через кривизнуk
и кручение
эвольвенты
регулярной кривой через кривизнуk
и кручение
 этой кривой.
этой кривой.
§7. Плоские кривые
Основные вопросы
Точки перегиба.
Особые точки кривой.
Асимптоты.
Соприкосновение кривых. Порядок соприкосновения. Соприкасающаяся окружность.
Огибающая семейства кривых.
Упражнения с решениями
Определить точки перегиба следующих кривых:
а)
 б)
б)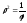 (жезл;
см.рис.18); в)
(жезл;
см.рис.18); в)
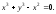
Решение.
а) Точка перегиба параметризованной
кривой x
= x(t),
y
= y(t)
характеризуется тем, что в ней кривизна
k
равна нулю, т.е.
 и
и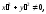 причем выражение
причем выражение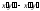 меняет в ней знак (см.§5,
п.II,
задача 5.). В данном случае имеем:
меняет в ней знак (см.§5,
п.II,
задача 5.). В данном случае имеем:
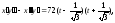
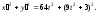
Первое
выражение обращается в нуль при
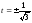 ,
причем его знак изменяется при переходе
через эти точки. Второе выражение отлично
от нуля. Итак,
,
причем его знак изменяется при переходе
через эти точки. Второе выражение отлично
от нуля. Итак,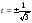 - параметры точек перегиба. Сами точки
перегиба - (
- параметры точек перегиба. Сами точки
перегиба - (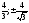 ).
).
б)
Поскольку кривизна k
кривой, заданной полярным уравнением
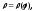 вычисляется по формуле
вычисляется по формуле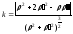 ( см.§5,
п.III,
задача 5
), решаем систему:
( см.§5,
п.III,
задача 5
), решаем систему:
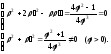
Так
как k=0
при
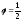 , и выражение
, и выражение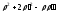 меняют
знак при переходе через точку
меняют
знак при переходе через точку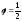 ,
то
,
то -
точка перегиба.
-
точка перегиба.
в)
Обозначим:
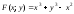 .
Тогда имеем:
.
Тогда имеем:
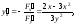
 ( учли, что
( учли, что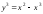 ).
).
Если
0<x<1,
то
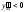 ,
и кривая выпукла вверх; еслиx>1,
то
,
и кривая выпукла вверх; еслиx>1,
то
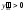 ,
и кривая выпукла вниз. Следовательно,
(1;0)
- точка перегиба кривой.
,
и кривая выпукла вниз. Следовательно,
(1;0)
- точка перегиба кривой.
Ответ:
а) (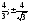 );
б)
);
б)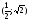 ;
в)(1;0).
;
в)(1;0).
Найти особые точки следующих кривых и указать их тип:
а)
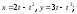 б)
б) в)
в)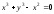 .
.
Решение.
а) Сначала ищем точки возврата. Имеем:
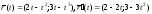 ,
следовательно,
,
следовательно,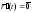 ,
еслиt=1.
Порядок первой отличной от нуля
производной функции
,
еслиt=1.
Порядок первой отличной от нуля
производной функции
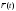 приt=1
будет четным
приt=1
будет четным
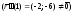 ,
поэтому точка с параметромt=1
- особая. Порядок первой из производных,
не коллинеарных при t=1
вектору
,
поэтому точка с параметромt=1
- особая. Порядок первой из производных,
не коллинеарных при t=1
вектору
 ,
будет нечетным (вектор
,
будет нечетным (вектор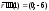 неколлинеарен
вектору
неколлинеарен
вектору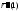 ),
поэтому найденная особая точка (ее
координаты - (1;2)) является точкой возврата
1-го рода (кривая расположена по обе
стороны от касательной в этой точке).
),
поэтому найденная особая точка (ее
координаты - (1;2)) является точкой возврата
1-го рода (кривая расположена по обе
стороны от касательной в этой точке).
Для
нахождения узловых точек (самопересечения,
самоприкасания) составляем уравнение
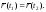 Нетрудно убедиться, что данное равенство
может иметь место в том и только том
случае, когда
Нетрудно убедиться, что данное равенство
может иметь место в том и только том
случае, когда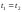 .
Следовательно, кривая не имеет узловых
точек.
.
Следовательно, кривая не имеет узловых
точек.
б)
В этом случае производная функции
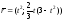 существует
и не обращается в нуль. Следовательно,
точек излома и возврата кривая не имеет.
существует
и не обращается в нуль. Следовательно,
точек излома и возврата кривая не имеет.
Уравнение
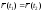 для
нахождения параметров
для
нахождения параметров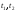 узловых
точек эквивалентно следующей системе:
узловых
точек эквивалентно следующей системе: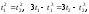
которая
имеет две пары решений, удовлетворяющих
условию
 .
Таким образом, значениям параметра
.
Таким образом, значениям параметра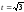 и
и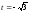 соответствует
одна и та же узловая точка на кривой -
(3;0).
соответствует
одна и та же узловая точка на кривой -
(3;0).
Поскольку
векторы
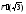 и
и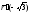 не
коллинеарны, то эта точка является
точкой самопересечения.
не
коллинеарны, то эта точка является
точкой самопересечения.
в)
Обозначим:
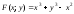 .
Так как
.
Так как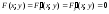 приx
= 0, y
= 0, то начало
координат является особой точкой.
приx
= 0, y
= 0, то начало
координат является особой точкой.
Вычисляем
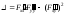 в точке (0;0):
в точке (0;0):
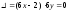 при x
= y
= 0. Это
означает, что (0;0) - либо изолированная
точка, либо точка возврата, либо точка
самоприкасания.
при x
= y
= 0. Это
означает, что (0;0) - либо изолированная
точка, либо точка возврата, либо точка
самоприкасания.
Чтобы
установить тип точки проведем
дополнительное исследование. При
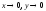 имеем:
имеем: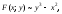 поскольку
поскольку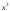 -
бесконечно малая высшего порядка по
сравнению с
-
бесконечно малая высшего порядка по
сравнению с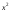 .
.
Следовательно,
строение данной кривой в окрестности
начала координат походит на строение
полукубической параболы
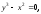 т.е
(0;0) - точка возврата 1-го рода.
т.е
(0;0) - точка возврата 1-го рода.
Ответ: а) (1;2) - точка возврата 1-го рода; б) (3;0) - точка самопересечения; в) (0;0) - точка возврата 1-го рода.
Найти асимптоты плоских кривых:
а)
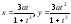 (декартов
лист);
(декартов
лист);
б)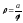 (гиперболическая спираль);
(гиперболическая спираль);
в)
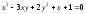 (гипербола).
(гипербола).
Решение.
а) Кривая уходит в бесконечность при
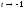 ,
поскольку
,
поскольку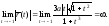 Ищем невертикальную асимптоту, уравнение
которой имеет видY
= kX+b:
Ищем невертикальную асимптоту, уравнение
которой имеет видY
= kX+b:
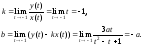
Итак, X+Y+a = 0 - невертикальная асимптота. Других асимптот нет.
б)
Пусть Oxy
- декартова система координат, согласованная
с полярной обычным образом. Так как
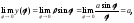 то прямаяy
= а - асимптота
(ее полярное уравнение -
то прямаяy
= а - асимптота
(ее полярное уравнение -
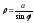 ).
Других асимптот нет.
).
Других асимптот нет.
Замечание.
Полюс является асимптотической точкой
гиперболической спирали, поскольку
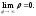
в)
Будем искать уравнение невертикальной
асимптоты в виде Y=kX+b.
Чтобы найти угловой коэффициент
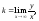 разделим обе части уравнения на
разделим обе части уравнения на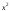 :
:
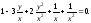
Переходя
к пределу при
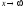 ,
имеем:
,
имеем:
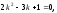
откуда
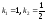 .
.
Для нахождения коэффициента b предварительно перепишем уравнение кривой в виде (y-x)(2y-x)+x+1=0. С учетом этого представления находим:
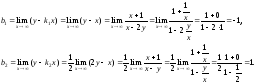
Итак,
невертикальные асимптоты данной кривой
имеют уравнения
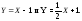 Других асимптот нет.
Других асимптот нет.
Ответ:
а) X+Y+a
= 0; б)
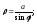 в)
в)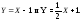
Написать уравнение соприкасающейся окружности кривой y = sinx в точке
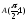 и
найти порядок соприкосновения.
и
найти порядок соприкосновения.
Решение.
Уравнение соприкасающейся окружности
может быть записано в виде
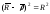 ,
где
,
где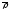 -
радиус-вектор центра окружности,
-
радиус-вектор центра окружности,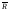 -
радиус-вектор ее текущей точки,R
- радиус. Последний равен радиусу кривизны
кривой y
= sinx
в точке А:
-
радиус-вектор ее текущей точки,R
- радиус. Последний равен радиусу кривизны
кривой y
= sinx
в точке А:
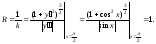
Находим
вектор центра:
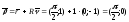 (здесь:
(здесь: -
радиус-вектор точки данной кривой,
-
радиус-вектор точки данной кривой,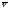 -
орт ее нормали (он направлен в сторону
вогнутости кривой)). Итак, уравнение
соприкасающейся окружности в точке А
имеет вид:
-
орт ее нормали (он направлен в сторону
вогнутости кривой)). Итак, уравнение
соприкасающейся окружности в точке А
имеет вид: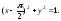 Чтобы найти порядок соприкосновения,
исключим из полученного уравненияy,
заменяя его по формуле
y
= sinx
:
Чтобы найти порядок соприкосновения,
исключим из полученного уравненияy,
заменяя его по формуле
y
= sinx
:
 Обозначая левую часть черезF(x),
имеем:
Обозначая левую часть черезF(x),
имеем:
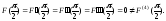
Таким образом порядок соприкосновения равен 3.
Ответ:
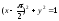 ;
3.
;
3.
Найти огибающую семейства кривых
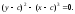
Решение. Составляем систему уравнений, определяющую координаты точек дискриминантной кривой.
Имеем:
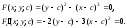
Чтобы исключить параметр с, перепишем полученную систему в виде:
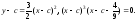
Отсюда
вытекает, что дискриминантная кривая
распадается на две ветви: y=x
и
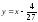 .Легко проверить,
что первая из них состоит из особых
точек кривых семейства (вдоль нее
.Легко проверить,
что первая из них состоит из особых
точек кривых семейства (вдоль нее
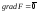 ),
а вторая - не содержит особых точек, т.е.
является огибающей.
),
а вторая - не содержит особых точек, т.е.
является огибающей.
Ответ:
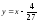 .
.
