- •Ю.П.Золотухин, а.А.Гринь Практикум по дифференциальной геометрии
- •Часть 1
- •Часть 1.
- •Содержание
- •Предисловие
- •Введение
- •§1. Вектор-функции
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •Часть I. Кривые на плоскости и в пространстве
- •§2. Способы задания кривых
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§3. Замечательные кривые
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§4. Касательная прямая. Длина дуги. Натуральная параметризация
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§5. Сопровождающий трехгранник. Кривизна и кручение
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§6. Формулы Френе. Натуральные уравнения. Эволюта и эвольвента
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§7. Плоские кривые
- •Основные вопросы
- •Упражнения с решениями
- •Упражнения и задачи для самостоятельной работы
- •§8. Дополнительные задачи
- •Группа в
- •1. Плоские алгебраические кривые третьего порядка
- •Литература а. Основные учебники
- •Б. Дополнительная литература учебного характера
- •В. Сборники задач
- •Г. Методические указания
- •Д. Литература справочно-энциклопедического характера
- •Е. Вводные курсы, научно-популярная литература
- •Ж. Литература по истории дифференциальной геометрии
1. Плоские алгебраические кривые третьего порядка
Рис.2. Циссоида
Диоклесса
Рис.3. Строфоида
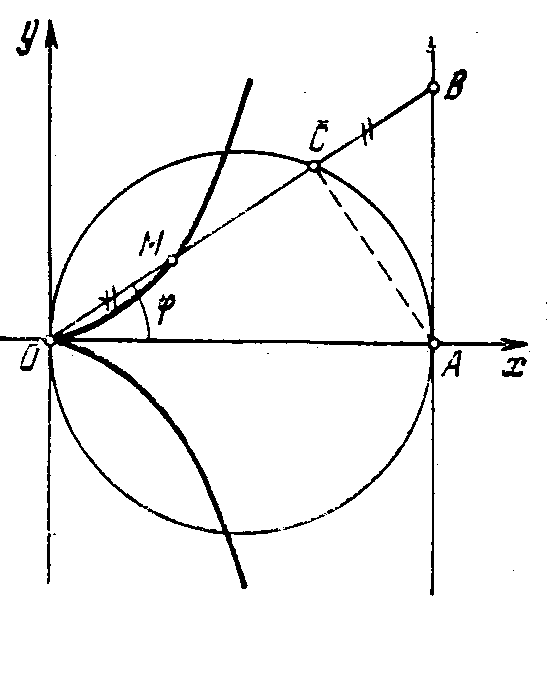
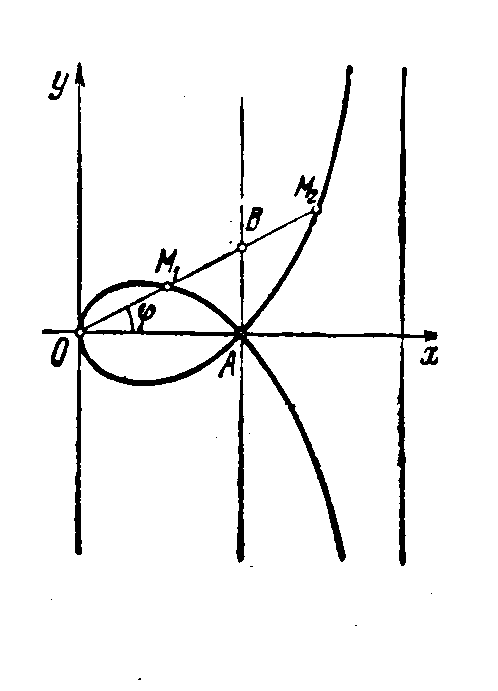
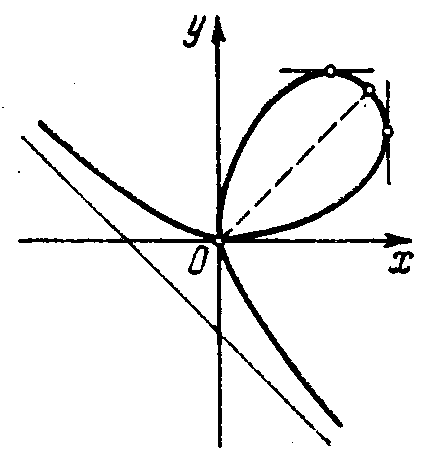 Рис.1. Декартов лист
Рис.1. Декартов лист
2. Плоские алгебраические кривые четвертого и высших порядков
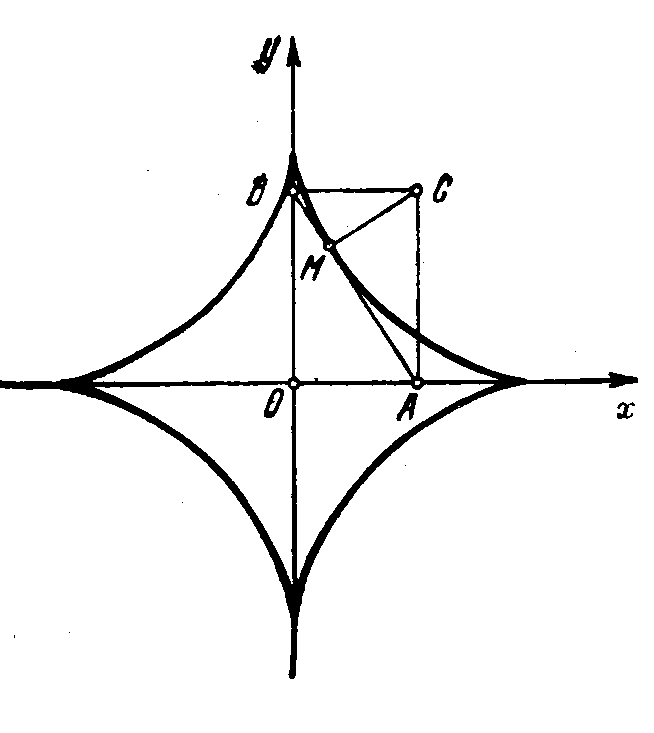
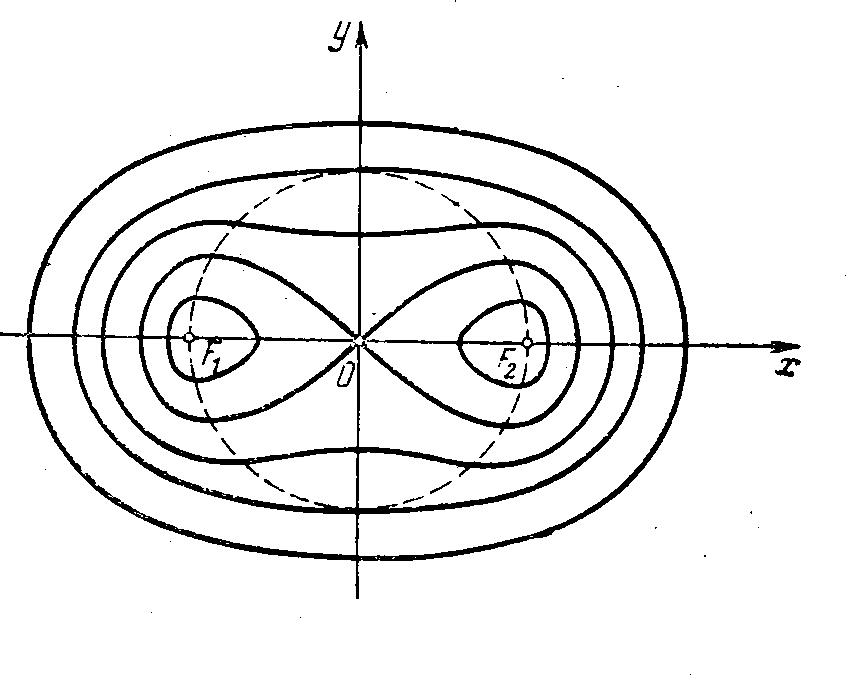
Рис. 4. Астроида Рис.5. Овалы Кассини
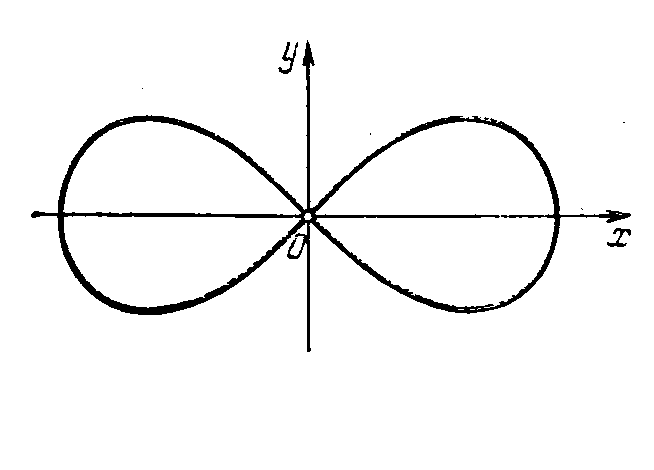
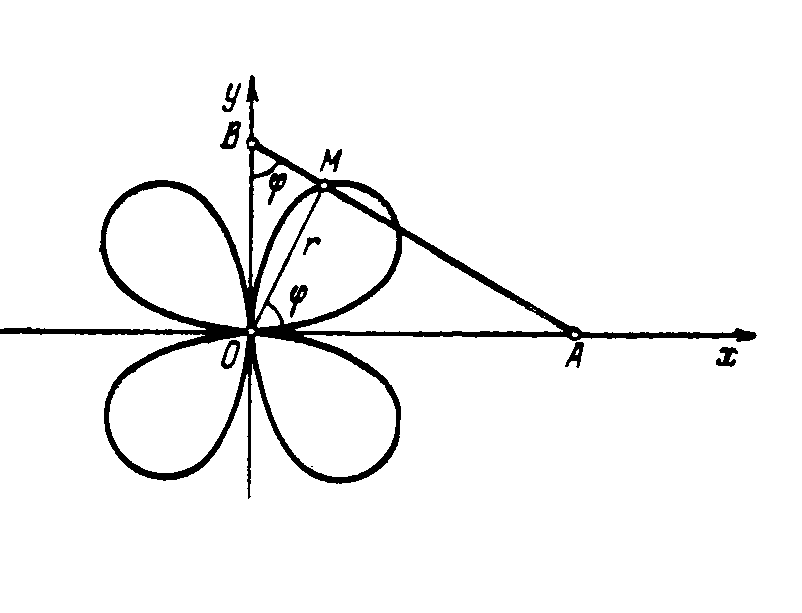
Рис.6. Лемниската Бернулли Рис. 7. Четырехлепестковая роза
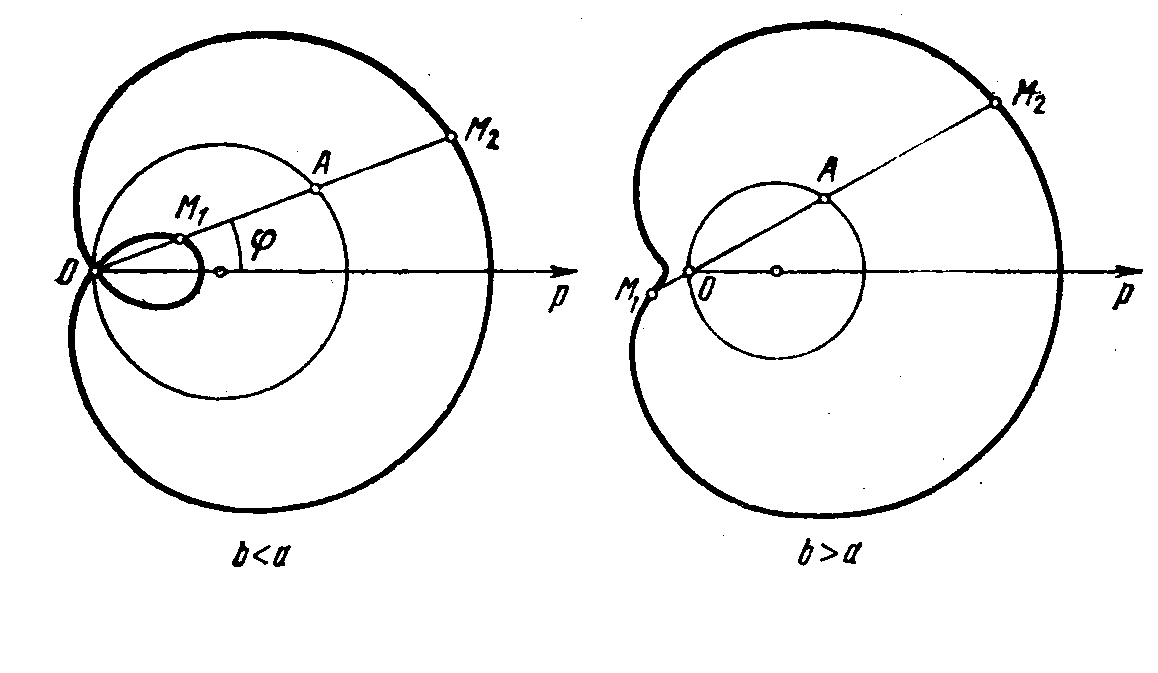
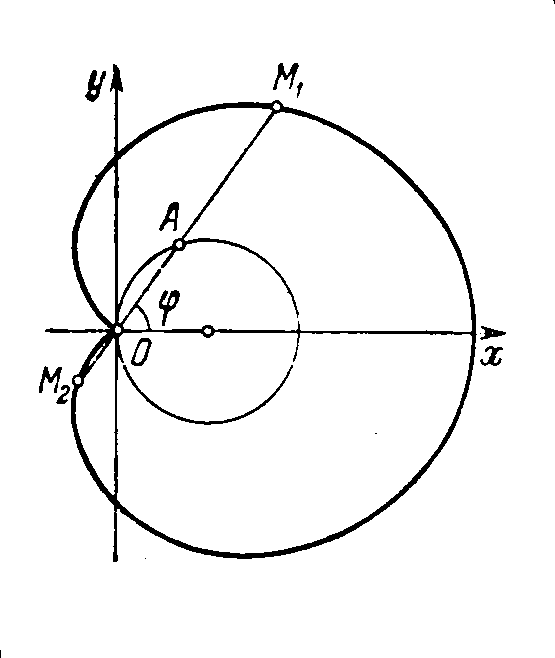
Рис. 8. Улитки Паскаля Рис.9. Кардиоида

Рис. 10. Эпициклоиды
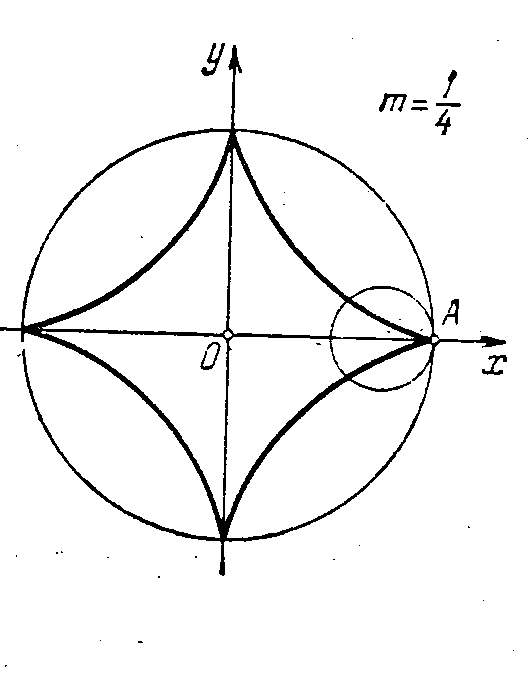

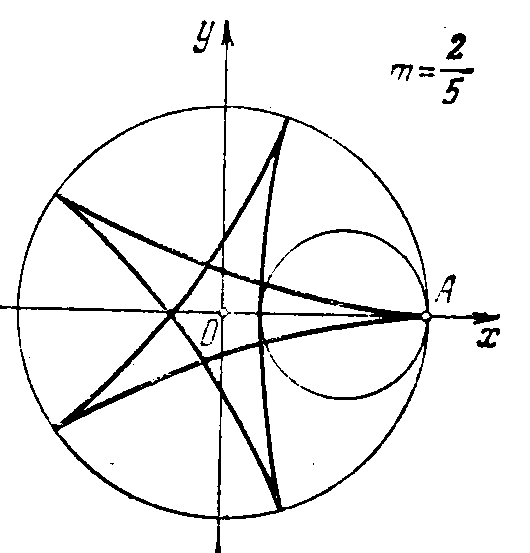
Рис. 11. Гипоциклоиды
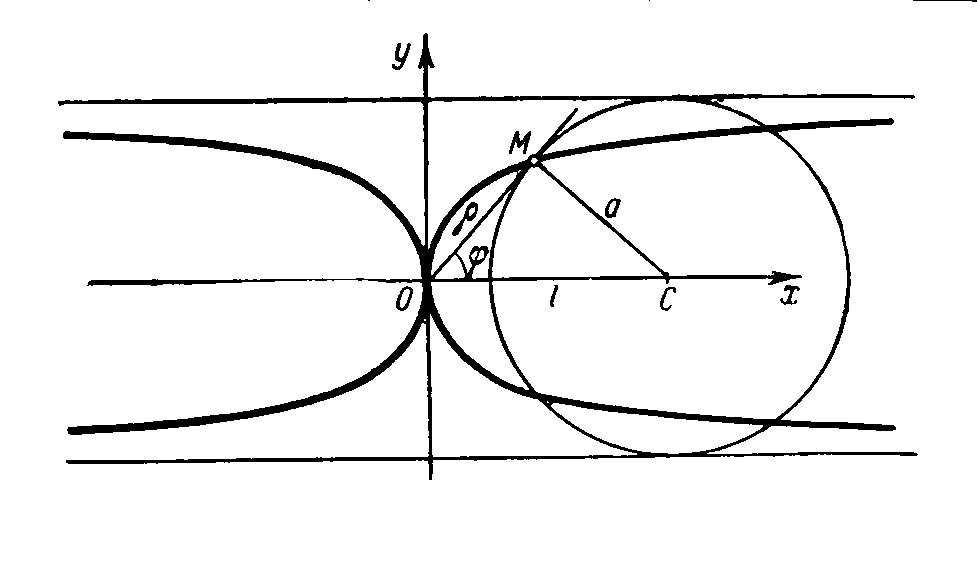
Рис. 12. Каппа
3. Плоские трансцендентные кривые
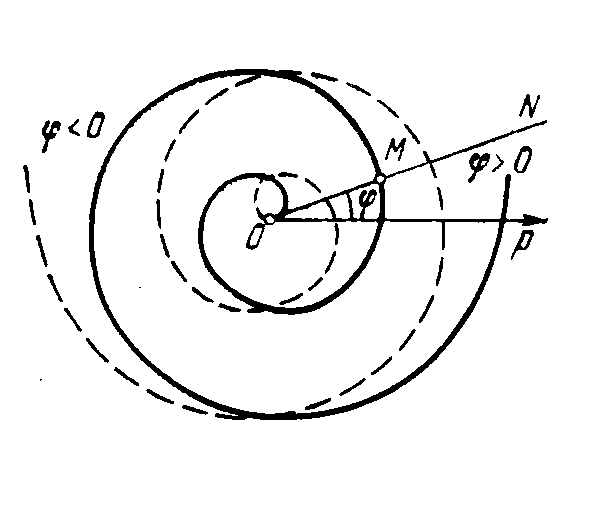
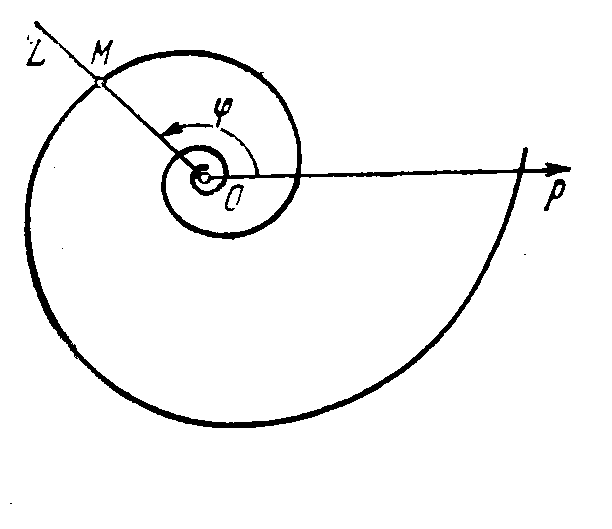
Рис. 13. Спираль Архимеда Рис. 14. Логарифмическая спираль
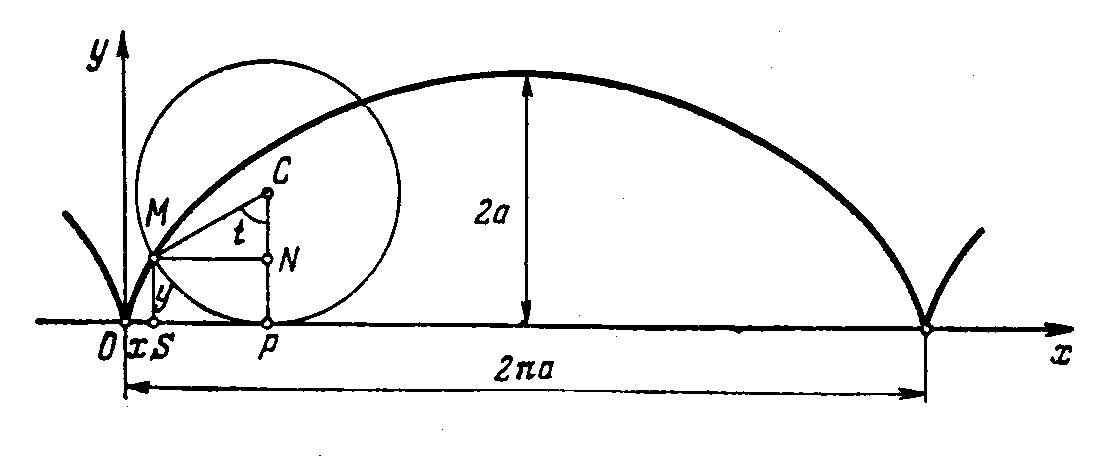
Рис. 15. Циклоида
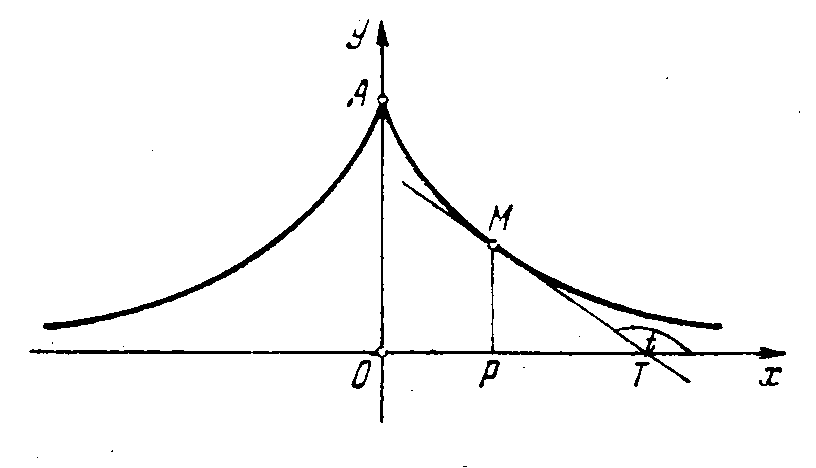
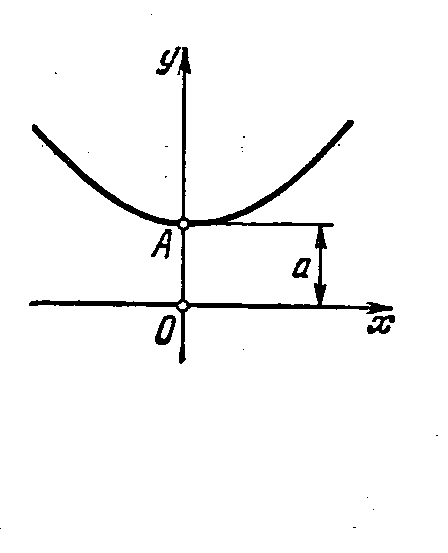
Рис. 16. Трактрисса Рис. 17. Цепная линия
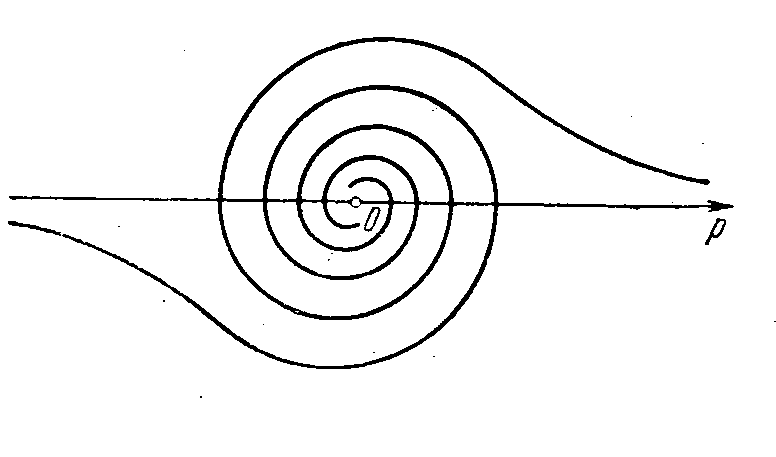
Рис. 18. Жезл
4. Пространственные кривые
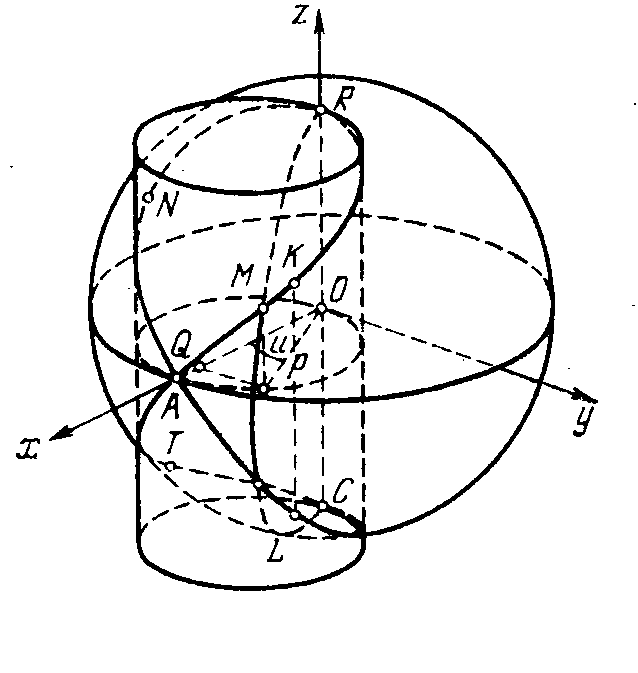
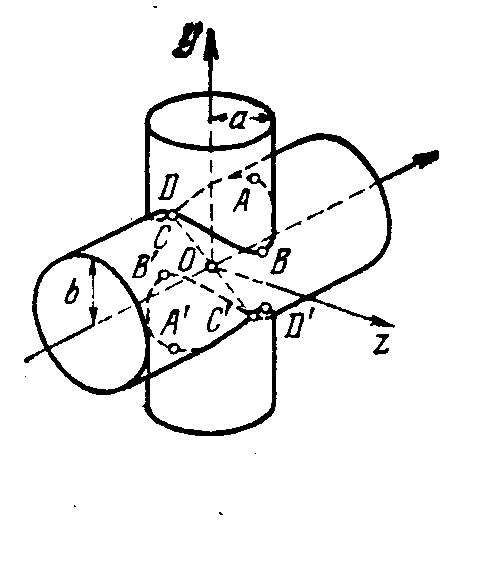
Рис. 19. Кривая Вивиани Рис. 20. Бицилиндрика
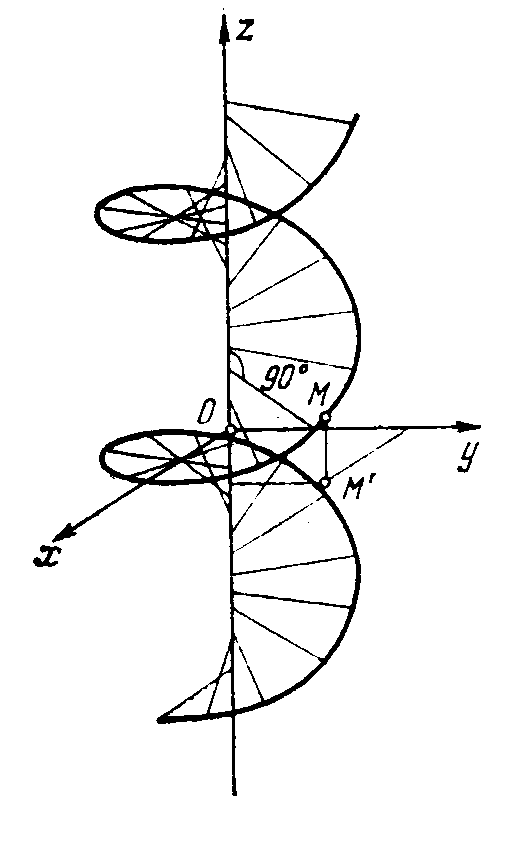
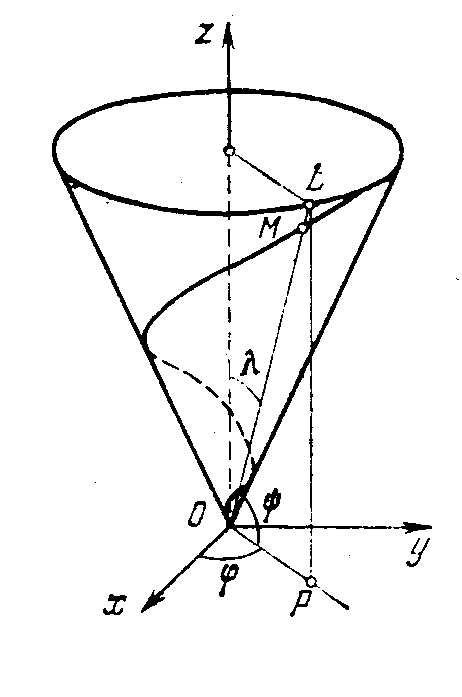
Рис. 21. Винтовая линия Рис. 22. Коническая винтовая линия
Ответы, указания, краткие решения
§1
а) Дуга окружности
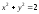 между точками (1;1) и
между точками (1;1) и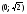 ;
б) Левая ветвь гиперболы
;
б) Левая ветвь гиперболы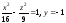 .
.а) (1;0;1); б)(4;-2).
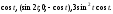
а)
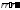 ;
б)
;
б)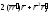 в)
в)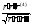
а) (1;1;2), (1;-1;2); б) -12х2y2; в)(3u2+5u4; 3u2-5u4; 16u15).
а)
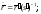 б)
б)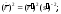 в)
в)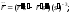 г)
г)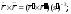 д)
д)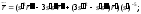 е)
е)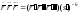 (точками обозначены производные по s).
(точками обозначены производные по s).
§2
а)
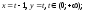 б)
б)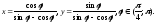
Замена переменной - диффеоморфизм
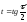 ,
,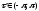 . Эллипс
. Эллипс
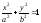 с выколотой точкой (-а;0).
с выколотой точкой (-а;0).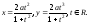 При изменении t
от -
При изменении t
от - до
+
до
+ точка движется по кривой снизу вверх.
(0;0) - особая точка неявного задания.
точка движется по кривой снизу вверх.
(0;0) - особая точка неявного задания.Одна из возможных параметризаций в случае, когда a<b:
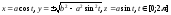 (Знакам «+» и «-» соответствуют различные
компоненты бицилиндрики).
(Знакам «+» и «-» соответствуют различные
компоненты бицилиндрики).
а)
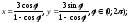 б)y2
=
6x+9.
б)y2
=
6x+9.а)
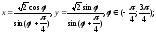 б)x+y-2
=
0.
б)x+y-2
=
0.
а)
 б)
б)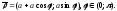 Параметризации
Параметризации и
и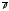 -
регулярные и эквивалентные (замена
параметра:
-
регулярные и эквивалентные (замена
параметра: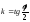 ).
).
7.
а)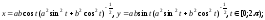 б)
б)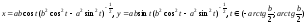 для правой ветви и
для правой ветви и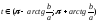 для
левой ветви; в)
для
левой ветви; в)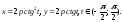
а) Окружность (xR)2+y2=R2 с выколотой точкой (0;0); б) Правая ветвь гиперболы
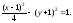
а) Окружность: x2+y2=13, z=6; б) Две пары пересекающихся прямых: x2-y2 = 0,
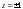 .
.y = shz, x = 0; x = chz, y=0(цепная линия(см.рис.17)); x2-y2=1, z = 0 (гипербола).
§3
Параметрические уравнения: x=asin2tcost, y=asin2tsint (t - угол между отрезком и положительной полуосью х); неявное уравнение: (x2+y2)3 = 4a2x2y2; полярное уравнение:
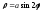 (полярные координаты согласованы с
декартовыми стандартным образом).
(полярные координаты согласованы с
декартовыми стандартным образом).Если выбрать в качестве полюса начало луча, а полярную ось провести через центр окружности, то полярное уравнение кривой будет иметь вид:
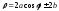 .Неявное уравнение:
(x2+y2-2ax)2
=
4b2(x2+y2).
.Неявное уравнение:
(x2+y2-2ax)2
=
4b2(x2+y2).Если выбрать в качестве полюса точку О и считать, что в начальный момент времени (t = 0) точка М находилась на полярной оси на расстоянии
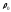 от
полюса, то полярное уранение кривой
будет иметь вид:
от
полюса, то полярное уранение кривой
будет иметь вид: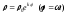 .
.Если принять прямую l за ось х, то параметрические уравнения кривой будут иметь вид:
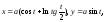 гдеt
- угол наклона касательной к оси х.
гдеt
- угол наклона касательной к оси х.Если в момент времени t = 0 точка М находится в начале системы координат, то параметрические уравнения кривой будут иметь вид:
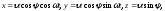 где
где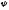 -
угол между прямойOL
и плоскостью z
= 0.
-
угол между прямойOL
и плоскостью z
= 0.Полярное уравнение:
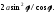 Параметрические уравнения:
Параметрические уравнения: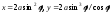 или
или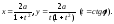 Неявное уравнение:x3
= y2(2ax).
Неявное уравнение:x3
= y2(2ax).Полярное уравнение:
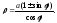 Параметрические уравнения:
Параметрические уравнения: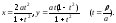 Неявное уравнение: (2a-x)y2
= x(xa)2.
Неявное уравнение: (2a-x)y2
= x(xa)2.Если поместить начало прямоугольной декартовой системы координат Oxy в центр неподвижной окружности и считать, что в исходном положении точка М совпадает с точкой (R;0), то параметрические уравнения кривой будут иметь вид:
x = (R+mR)cosmtmRcos(t+mt), y = (R+mR)sinmtmRsin(t+mt), где t - угол между радиусом катящейся окружности, оканчивающимся в точке М, и радиальной осью окружностей, r = mR. При r = R получим кардиоиду.
9. x = (R-mR)cosmt+mRcos(t-mt), y = (R-mR)sinmt-mRsin(t-mt),r=mR. При R = 4r получим астроиду.
§4
а)Y=X, Y= X; б) 2Xsint+2Ycostasin2t = 0, Xcost-Ysintacos2t = 0; в)
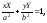
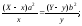 г)Y
= a;
X
= a;
д)
г)Y
= a;
X
= a;
д)

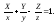
а)
 б)
б)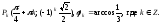
а)
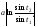 где
где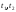 -
углы, образованные с осьюх
касательными,
проведенными в концах дуги (см. §3,
п.III,
задача 4 и рис.16); б)16r;
в)9а.
-
углы, образованные с осьюх
касательными,
проведенными в концах дуги (см. §3,
п.III,
задача 4 и рис.16); б)16r;
в)9а. а)
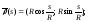 б)
б)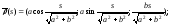 в)
в)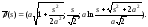
а)
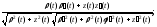 б)
б)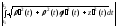
а)
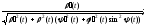 б)
б)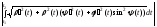
а)
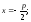 б)
б)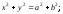 в)
в)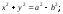
8.
Гиперболические спирали
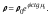
10.
§5
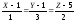 (касательная),
(касательная),
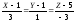 (бинормаль),
(бинормаль),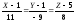 (главная нормаль);
(главная нормаль); (нормальная
плоскость),
(нормальная
плоскость),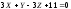 (соприкасающаяся
плоскость),
(соприкасающаяся
плоскость),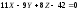 (спрямляющая плоскость).
(спрямляющая плоскость).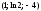
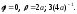 Точек спрямления
нет.
Точек спрямления
нет.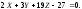
6. Винтовая линия
9.
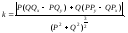
10.
Точки спрямления
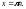 Точки уплощения
Точки уплощения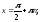
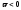 при
при
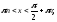
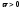 при
при
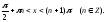
§6
а)
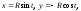 где
где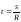 (окружность);
(окружность);
б)
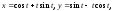 где
где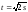 (эвольвента
окружности радиуса 1).
(эвольвента
окружности радиуса 1).
а)
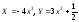 (полукубическая парабола);
(полукубическая парабола);
б) Если
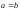 ,
эволюта - точка, центр данной окружности.
,
эволюта - точка, центр данной окружности.
Если
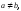 то
то
а)
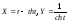 (трактриса). (Стандартные параметрические
уравнения можно получить перейдя к
параметру
(трактриса). (Стандартные параметрические
уравнения можно получить перейдя к
параметру )
)
б)
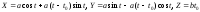 (
( -
произвольная
-
произвольная
постоянная).
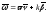 Вектор
Вектор
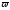 есть
мгновенная угловая скорость репера
Френе при движении вдоль кривой с
единичной скоростью.
есть
мгновенная угловая скорость репера
Френе при движении вдоль кривой с
единичной скоростью.
8.
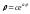 (логарифмическая спираль).
(логарифмическая спираль).
10.
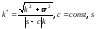 -
натуральный параметр точки.
-
натуральный параметр точки.
§7
а) (1;1); б)
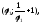 где
где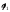 -
корень уравнения
-
корень уравнения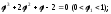 в)
в)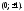
а) (0;0) - точка возврата 2-го рода;
б)
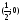 -
точка самопересечения;
-
точка самопересечения;
в) (0;0) - изолированная точка.
а)
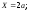 б)
б)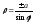 (прямые,
параллельные полярной оси); в)
(прямые,
параллельные полярной оси); в)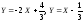 .
.
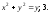
x=0, y=0.
8.
x=0,
y=0,
пара
гипербол
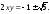
§8
Положим
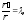 где
где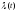 -
непрерывная на отрезке [a;b]
функция, сохраняющая определенный
знак. Имеем:
-
непрерывная на отрезке [a;b]
функция, сохраняющая определенный
знак. Имеем: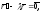 откуда
откуда
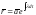 ,
где
,
где .
Так как производная от функции
.
Так как производная от функции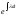 равна
равна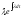 ,
то она сохраняет знак на отрезке [a;b],
т.е.
,
то она сохраняет знак на отрезке [a;b],
т.е.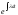 - монотонная и непрерывная функция
t.
- монотонная и непрерывная функция
t.
Пусть
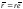 ,
где
,
где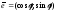 .
.
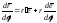 .
.
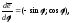 т.е.
т.е.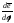 получается
из
получается
из поворотом на угол
поворотом на угол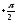 .
Обозначим вектор, получающийся из
.
Обозначим вектор, получающийся из поворотом
на
поворотом
на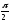 ,
через
,
через .
.
Следовательно,
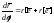 .
Далее:
.
Далее:
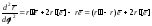 ,
,
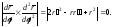
Полагая
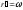 ,
находим:
,
находим:
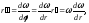
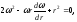
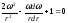 .
.
Полагая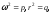 имеем
уравнение
имеем
уравнение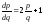 .
Решая его, находим:
.
Решая его, находим: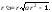 Окончательно имеем :
Окончательно имеем :
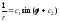 или
или
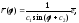
где
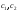 -
произвольные числа.
-
произвольные числа.
а) Имеем:
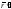 и
и -
параллельны, т.е.
-
параллельны, т.е.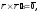 тогда
тогда ;
следовательно,
;
следовательно,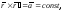
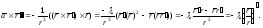
Итак,
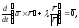
и
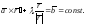
Умножая обе части
последнего равенства скалярно на
 и учитывая, что
и учитывая, что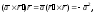 получим:
получим: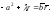 Так как из соотношения
Так как из соотношения следует, что
следует, что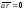 ,
то кривая лежит в плоскости, перпендикулярной
вектору
,
то кривая лежит в плоскости, перпендикулярной
вектору .
Если ввести в этой плоскости полярную
систему координат, совместив полюс с
началом радиус-векторов и направляя
полярную ось по вектору
.
Если ввести в этой плоскости полярную
систему координат, совместив полюс с
началом радиус-векторов и направляя
полярную ось по вектору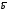 ,
найдем:
,
найдем:
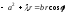 ,
т.е.
,
т.е.
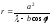 .
.
б) Окружности,
центры которых расположены на прямой,
проходящей через начало радиус-векторов
коллинеарно вектору
 ,
а плоскости этих окружностей перпендикулярны
к указанной прямой.
,
а плоскости этих окружностей перпендикулярны
к указанной прямой.
в)Прямые, по которым
пересекаются плоскости, перпендикулярные
вектору
 ,
с плоскостями, проходящими через прямую,
проведенную через полюс коллинеарно
вектору
,
с плоскостями, проходящими через прямую,
проведенную через полюс коллинеарно
вектору .
.
Радиус-вектор
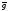 произвольной
точки неподвижной центроиды может быть
определен следующими соотношениями:
произвольной
точки неподвижной центроиды может быть
определен следующими соотношениями:
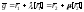 .
.
Далее имеем:


Следовательно,

Рассмотрим вектор
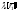 ,
где
,
где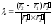 .
.
Если
этот вектор отложить от конца вектора
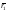 ,
то его конец попадет в мгновенный центр
вращения. Проекции вектора
,
то его конец попадет в мгновенный центр
вращения. Проекции вектора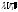 на векторы
на векторы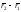 и
и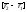 соответственно равны:
соответственно равны:
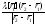 и
и

Поэтому уравнения подвижной центроиды имеют вид:
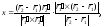
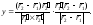
6.
а) Возьмем начало системы координат
(не обязательно прямоугольной) в точке
с радиус-вектором
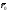 ,
а векторы
,
а векторы и
и примем за базисные векторы осейх
и y.
Тогда параметрические уравнения кривой
будут x=t,
y=t2,
т.е. y=x2.
Следовательно, имеем уравнение параболы.
В случае коллинеарности векторов
примем за базисные векторы осейх
и y.
Тогда параметрические уравнения кривой
будут x=t,
y=t2,
т.е. y=x2.
Следовательно, имеем уравнение параболы.
В случае коллинеарности векторов
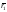 и
и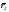 получим
прямую или полупрямую.
получим
прямую или полупрямую.
б)
Эллипс. В случае коллинеарности векторов
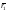 и
и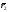 - отрезок прямой.
- отрезок прямой.
в)
Ветвь гиперболы. В случае коллинеарности
векторов
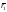 и
и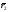 - луч или прямая.
- луч или прямая.
Так как пучок проектирующих прямых параллелен плоскости yz, то уравнения проекции будут иметь вид:
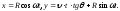
Проекция
будет иметь особые точки (точки возврата
первого рода), если
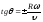 .
.
Уравнение подэры будем искать в виде
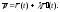
Параметр
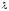 найдем из условия
найдем из условия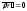 :
:
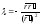
Таким
образом,
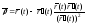 .
.
Так как для винтовой линии
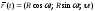 ,
то:
,
то:
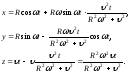
Искомая подэра лежит на однополостном гиперболоиде, уравнение которого
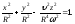
Возьмем уравнение параболы в виде
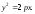
Касательная к параболе в точке
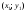 имеет
уравнение
имеет
уравнение
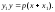 (1)
(1)
Пусть А(0;с) - точка на касательной, проведенной к вершине параболы, тогда
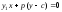 (2)
(2)
- перпендикуляр к касательной, проведенный из точки А. Кроме того,
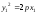 .
(3)
.
(3)
Координаты точки пересечения прямых (1) и (2):
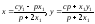 .
(4)
.
(4)
Исключая из равенств
(3) и (4) величины
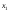 и
и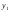 ,
получим уравнение искомой подэры:
,
получим уравнение искомой подэры:
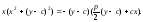
В(
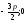 )
- точка на оси параболы, симметричная
фокусу. Уравнение трисектрисы
)
- точка на оси параболы, симметричная
фокусу. Уравнение трисектрисы
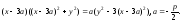
Применить теорему Ролля к функции
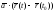 ,
где
,
где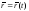 - параметризация кривой
- параметризация кривой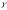 .
.
Выберем систему координат так, как указано на рисунке, где точка А - вершина циклоиды. Параметрические уравнения циклоиды в данном случае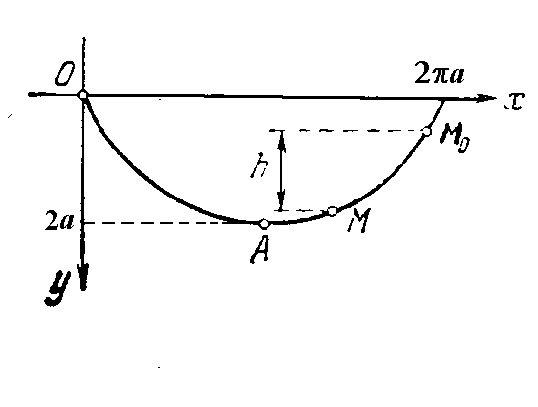
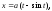
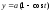 .
Скорость падающего тела определяется
по формуле
.
Скорость падающего тела определяется
по формуле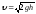 ,
гдеg
- ускорение свободного падения. В нашей
задаче
,
гдеg
- ускорение свободного падения. В нашей
задаче
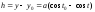 ,
,
где
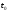 и
и соответствуют
точкам
соответствуют
точкам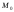 и
и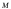 кривой.
кривой.
Отсюда
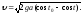
С
другой стороны скорость
 есть производная путиs
по времени Т:
есть производная путиs
по времени Т:
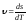
Поскольку
для циклоиды
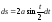 ,
то для определения времени Т получаем
дифференциальное уравнение
,
то для определения времени Т получаем
дифференциальное уравнение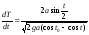 .
.
Интегрируя
его, находим время Т, затрачиваемое
материальной точкой на перемещение из
точки
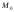 в точку А:
в точку А:
 .
.
За начало радиус-векторов возьмем точку М, ось абсцисс совместим с общей касательной l (см. рисунок).
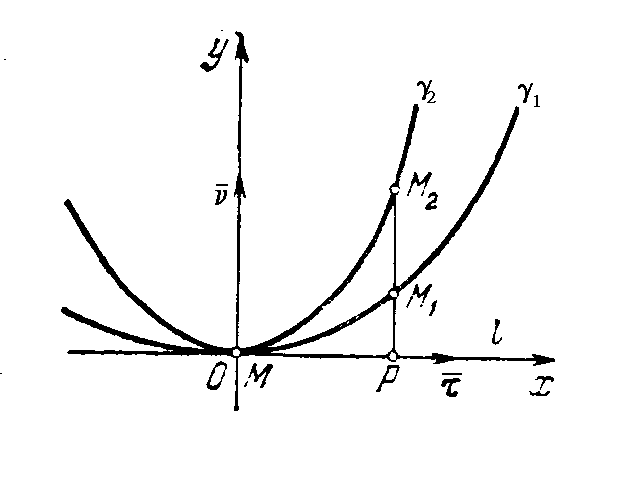
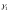 имеет параметризацию
имеет параметризацию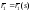 ,
гдеs
- длина дуги этой кривой, отсчитываемой
от точки М. Запишем уравнения кривой
,
гдеs
- длина дуги этой кривой, отсчитываемой
от точки М. Запишем уравнения кривой
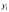 относительно
репера Френе, взятого в точке М. Подставляя
в разложение
относительно
репера Френе, взятого в точке М. Подставляя
в разложение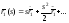 выражения
выражения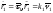 ,
получаем
,
получаем
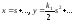 (1)
(1)
Аналогично
для кривой
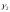
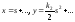 (2)
(2)
Если
Р - точка на касательной l,
близкая к точке М, и перпендикуляр к l,
проведенный в точке Р, пересекает кривые
 в точках
в точках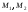 соответственно, то из уравнений (1), (2)
получаем
соответственно, то из уравнений (1), (2)
получаем
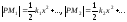
Поскольку
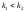 ,
то
,
то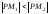 .
.
Имеем:
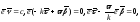
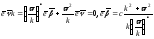 .
.
Дифференцируя еще раз, получаем требуемое соотношение. Заметим, что в силу приведенных выше равенств, можно считать, что
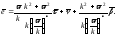
Если выполнено соотношение
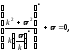
то
 -
постоянный вектор, образующий с вектором
-
постоянный вектор, образующий с вектором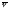 угол, косинус которого равен
угол, косинус которого равен
Докажем, что из свойства (1) вытекают свойства (2), (3) и (4).
Пусть
кривая
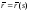 удовлетворяет
свойству (1), т.е. ее касательная образует
постоянный угол
удовлетворяет
свойству (1), т.е. ее касательная образует
постоянный угол с направлением, задаваемым ортом
с направлением, задаваемым ортом .
Тогда
.
Тогда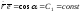 ,
или, что то же самое,
,
или, что то же самое,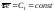 .
.
Дифференцируя
полученное равенство по натуральному
параметру s,
имеем:
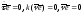 .
Последнее означает, что главные нормали
кривой параллельны плоскости, для
которой вектор
.
Последнее означает, что главные нормали
кривой параллельны плоскости, для
которой вектор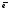 -
нормальный. Таким образом, свойство (2)
выполняется.
-
нормальный. Таким образом, свойство (2)
выполняется.
Далее
находим:
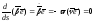 ,
т.е.
,
т.е. .Итак,
свойство (3) также выполняется.
.Итак,
свойство (3) также выполняется.
Наконец,
дифференцируя равенство
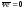 ,
,
получаем:
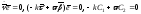 .
.
Поэтому
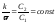 ;
свойство (4) имеет место.
;
свойство (4) имеет место.
а)
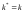 .
Если А* -
центр кривизны косой окружности
.
Если А* -
центр кривизны косой окружности
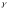 в
точке А,
в
точке А,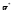 -
кручение
-
кручение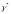 в
точке А* .
Если
в
точке А* .
Если
 -
кручение
-
кручение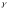 в
точке А, то
в
точке А, то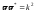 ,
т.е.
,
т.е.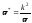 .
.
б)
Косая окружность
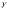 .
.
Уравнения кривых Бертрана можно записать в виде
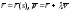 .
(1)
.
(1)
Так
как
 и
и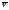 перпендикулярны,
то
перпендикулярны,
то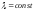 .
Из условия компланарности векторов
.
Из условия компланарности векторов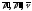 получаем:
получаем:
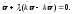
Разделив
последнее равенство на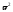 ,
имеем:
,
имеем:
 (2)
(2)
откуда
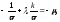
и, окончательно,
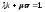 (3)
(3)
Обратно.
Из (3) следует (2).Подставляя значение
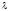 из (2) в (1), получаем уравнение искомой
линии.
из (2) в (1), получаем уравнение искомой
линии.
Так как расстояние между двумя точками кривой эквивалентно длине дуги
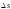 между ними, то задача сводится к
вычислению кратчайшего расстояния
между прямыми
между ними, то задача сводится к
вычислению кратчайшего расстояния
между прямыми
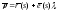 и
и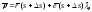
где
вектор
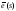 последовательно
равен
последовательно
равен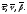
Кратчайшее расстояние вычислим по формуле
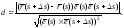
При
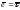

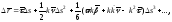
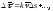
откуда
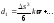 .
.
т.е.
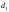 -
третьего порядка малости, если
-
третьего порядка малости, если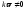 .
Аналогично можно найти, что
.
Аналогично можно найти, что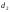 и
и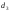 - первого порядка малости.
- первого порядка малости.
Если
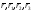 -
радиус-векторы точек кривых, то
-
радиус-векторы точек кривых, то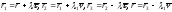 ,
,
где
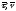 -
единичные векторы касательной и нормали
кривой
-
единичные векторы касательной и нормали
кривой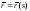 .
При этом
.
При этом
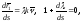
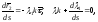

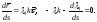
Отсюда
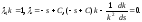
Следовательно,
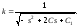
Получили
натуральное уравнение кривой
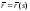 ,
которое определяет ее с точностью до
положения на плоскости.
,
которое определяет ее с точностью до
положения на плоскости.
Выберем в заданной вертикальной плоскости систему координат Oxy, поместив начало координат в заданную точку и направив ось у вертикально вверх (см. рисунок). Тогда параметрические уравнения кривых семейства будут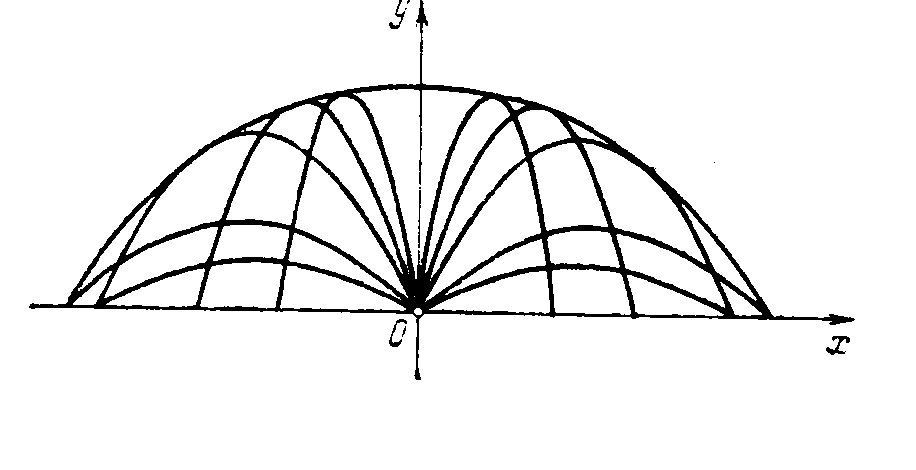
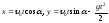 ,
где
,
где -
параметр семейства,
-
параметр семейства, -
ускорение свободного падения. Имеем:
-
ускорение свободного падения. Имеем:
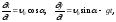
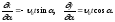
Приравнивая
нулю якобиан
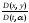 ,
получаем
,
получаем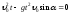 ,
откуда
,
откуда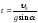 ,
и параметрические уравнения дискриминанты
имеют вид
,
и параметрические уравнения дискриминанты
имеют вид
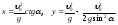
Исключив
 ,
получим
,
получим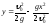
Дискриминанта
является огибающей и представляет собой
параболу безопасности, ось которой
направлена вертикально вниз по оси у,
параметр равен
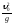 ,
а вершина находится в точке
,
а вершина находится в точке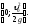
27.