127838-229237

Рис. 2.64

291

Для того чтобы получить действительное изображение Луны на экране, необходимо передвинуть окуляр вправо по ходу распространения световых лучей, увеличивая тем самым длину трубы, так, чтобы A′B′ было расположено на расстоянии, большем (по модулю) фокусного расстояния окуляра (рис. 2.64 б). Запишем формулу тонкой линзы, соответствующую этому случаю:

Из рис. 2.64 б видно, что искомое расстояние l , на которое необходимо передвинуть окуляр, будет равно:

Dl = a1¢¢ - a1¢ = 4,30 - 3,45 = 0,85 см.

Определим размер полученного на экране изображения. Из рис. 2.64 б следует геометрическое соотношение:

где a л – угловой размер Луны. Знак «–» означает, что изображе-

ние A′B′ является перевернутым относительно исходного предмета AB . Поскольку угол a л очень мал, то выражение (6) примет вид:

С учетом соотношения (7), выражение (8) примет окончательный вид:

Пример 32. Близорукий человек носит очки с оптической силой –2,0 дптр. На каком расстоянии от лица он должен держать выпуклое сферическое зеркало радиусом 0,30 м, чтобы резко видеть в зеркале свое изображение без очков?

293

Дано:

D0 = -2,0 дптр,

R = 30 см = 0,30 м.

Найти: l .

Решение. В соответствии с условием задачи при использовании очков с оптической силой D0 близорукий человек получает резкое изображение на сетчатке предмета, расположенного на расстоянии наилучшего зрения ( L0 = 25 см) от него. Соответственно без очков он будет отчетливо (резко) видеть предметы, расположенные на меньшем расстоянии a1 . Кроме того, учтем, что очки

расположены в непосредственной близости от глаз человека, поэтому будем рассматривать оптическую систему «хрусталик – линза очков» как две линзы, сложенные вплотную. В этом случае мы можем приближенно считать, что оптическая сила системы будет равна сумме оптических сил отдельных линз. Формула тонкой линзы [21.3] для двух случаев будет иметь вид:

1 + 1 (1)

L0 a2

где a2 – расстояние от хрусталика глаза (собирающей линзы) до сетчатки, D – оптическая сила глаза близорукого человека.

Вычитая из (1) соотношение (2), определим расстояние a1 , на

котором должен находиться предмет, чтобы близорукий человек видел его отчетливо:

Выпуклое зеркало человек должен держать на таком расстоянии a1′ , чтобы его изображение в зеркале получилось на расстоя-

294

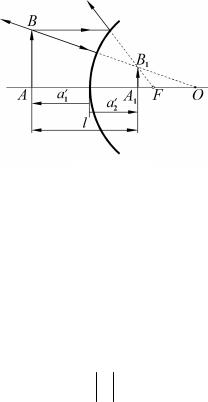
нии, равном a1 от его глаз. Для определения a1′ запишем формулу сферического зеркала [21.2]:

Рис. 2.65

После подстановки числовых значений a1 = −0,17 м и R = 0,30 м в

(4) и, обозначив a1′ = x , имеем уравнение второй степени относительно искомой величины:

Решая уравнение (5), получим: x1 = 0,237 и x2 = −0,107 .

Поскольку в соответствии с принятым правилом знаков расстояние a1′ < 0 , то физический смысл будет иметь только корень

x2 = −0,107 , то есть a1′ = −0,107 м. В таком случае расстояние от зеркала до лица будет равно l = a1′ = 0,107 м.

Ответ: l = 0,107 м.

295

Пример 33. Найти концентрацию свободных электронов в среде, если для радиоволн с частотой 150 МГц ее показатель преломления равен 0,92.

Дано:

ν = 150 МГц = 1,50×108 Гц, n = 0,92 .

Найти: N .

Решение. В соответствии с формулой дисперсии [22.12]:

Искомая концентрация свободных электронов выразится из соотношения (2) в виде:

N = e0 m(1 - n2 )(2pn)2 . e2

Подставляя числовые значения величин, получим:

N = 8,85 ×10−12 × 9,1×10−31( (1 - 0,92)2 )(2 × 3,14 ×1,50 ×108 )2 = 4,29 ×1013 м-3. 1,6 ×10−19 2

Ответ: N = 4,29 ×1013 м-3.

Пример 34. Показатель преломления воздуха при нормальном давлении и температуре 273 К для желтой линии натрия равен

296

1,0002918. Определить показатель преломления воздуха при температуре 30 °С и давлении 3,0 ×106 Па.

Дано:

λ = 589,3 нм = 589,3 ×10−9 м, n0 =1,0002918 ,

t = 30 °С, T = 303 К, T0 = 273 К,

p = 3,0×106 Па, p0 =1,0 ×105 Па.

Найти: n .

Решение. В соответствии с классической теорией дисперсии, показатель преломления газа зависит от концентрации N и поляризуемости α его молекул [22.13]:

Откуда можно получить соотношение показателей преломления при заданных и нормальных условиях:

Поскольку показатель преломления воздуха мало отличается от единицы, то можно воспользоваться приближением:

n2 -1 » 2(n -1).

Поэтому соотношение (2) с учетом приближения примет вид:

На основании молекулярно-кинетической теории связь между давлением газа, концентрацией молекул и абсолютной температурой имеет вид:

при давлении p и температуре T . Из соотношений (4) и (5) получим:

Подставив полученное соотношение (6) в (3), получим окончательно:

n =1 + pT0 (n0 -1) . Tp0

Подставляя числовые значения, получим:

Ответ: n = 1,00789 .

Пример 35. Два николя* расположены так, что угол между их

плоскостями поляризации составляет 60o . Определить, во сколько раз уменьшится интенсивность естественного света при прохождении через первый николь; во сколько раз уменьшится интенсивность естественного света при прохождении через два николя? При прохождении света через каждый николь потери на отражение и поглощение составляют 5,0 %.

Дано: a = 60o ,

k = 0,050 .

Решение. Призма Николя пропускает только одну составляющую поляризации света. Для естественного света она составляет половину интенсивности падающего света. Интенсивность

* Николем называют поляризационную призму Николя, которая позволяет получать из естественного свет линейно поляризованный.

298

света, прошедшего через первый поляризатор, с учетом поглощения и рассеяния, равна [22.9]:

интенсивность естественного света.

Относительное уменьшение интенсивности света при его прохождении через первый николь получим, разделив интенсивность I0 на интенсивность I1 поляризованного света:

второй николь (анализатор), определяется формулой Малюса

[22.14]:

проходящего через первый николь и падающего на второй николь, α – угол между плоскостью колебаний в поляризованном пучке и плоскостью пропускания второго николя.

Учитывая потери интенсивности во втором николе, выраже-

Уменьшение интенсивности при прохождении света через оба николя будет равно:

Учитывая (2), окончательно получим:

299

Подставляя числовые данные, имеем:

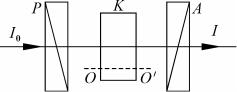
Пример 36. Пластинка кварца толщиной 1,0 мм, вырезанная перпендикулярно оптической оси и помещенная между двумя параллельными николями, поворачивает плоскость поляризации на

угол 20o (рис. 2.66). При какой толщине кварцевой пластинки свет этой же длины волны не будет выходить из второго николя?

Дано:

d ′ = 1,0 мм =1,0 ×10−3 м, a¢ = 20o .

Найти: d .

Решение. В соответствии с законом Малюса [22.14] интенсивность света, прошедшего через анализатор A , равна

где α – угол, который составляет плоскость поляризации падающего света, с плоскостью поляризации анализатора.

Если поляризатор P и анализатор A расположены параллельно, то при отсутствии пластинки K свет будет проходить без ослабления ( I = I0 ), поскольку α = 0 .

Рис. 2.66

300