
Дифференциальные уравнения 1
.pdf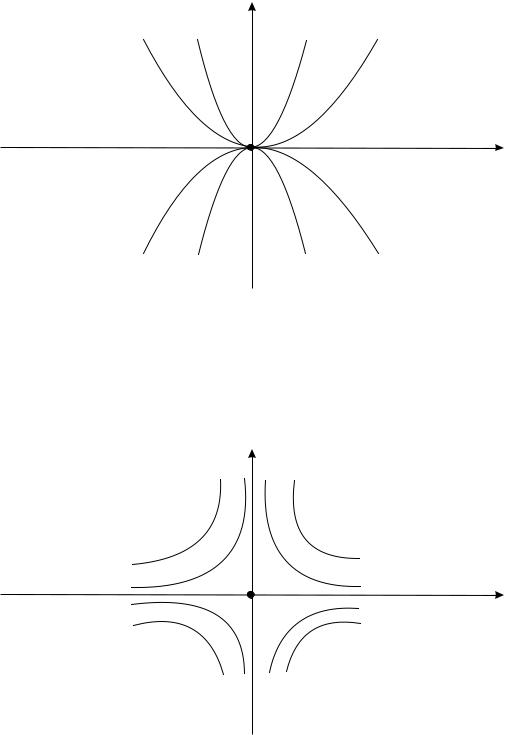
Картина расположения траекторий имеет специальное название – узел (бикритический узел) и при |λ2| > |λ1| изображена на рис. 39.1.
Y2
O |
Y1 |
|
Рис. 39.1.
2. Собственные числа λ1 и λ2 матрицы A вещественны и λ1λ2 < 0. Полученные в случае узла формулы сохраняют силу. Соответствующая геометрическая картина, называемая седлом, изображена на рис. 39.2.
Y2
O |
Y1 |
|
Рис. 39.2.
3. Собственные числа λ1 и λ2 матрицы A являются
181
комплексно сопряженными. Пусть λ1,2 = α ± iβ, β > |
|||
( |
β |
α |
) |
0. В данном случае J = |
α |
−β |
. Переходя к полярным |
координатам по формулам
y1 = ρ cos φ, y2 = sin φ,
получаем дифференциальную систему (У–31)
dρdt = αρ, dφdt = β.
Поэтому параметрические уравнения траекторий имеют вид
ρ = C1eαt, φ = βt + C2.
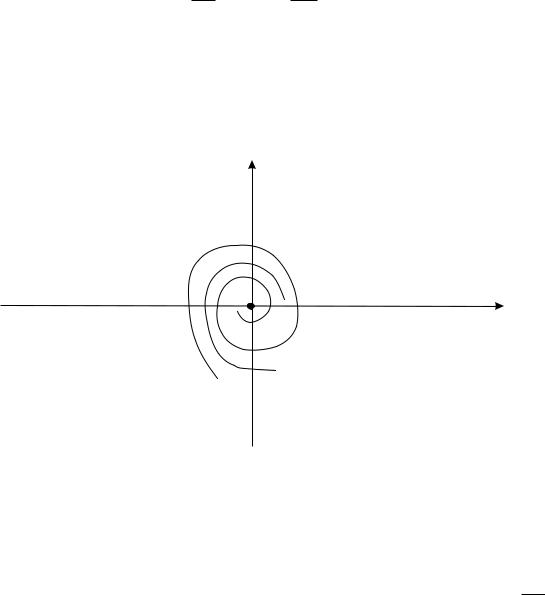
При αC1 ≠ 0 траектории образуют спирали (рис. 39.3). Такое
Y2
O |
Y1 |
Рис. 39.3.
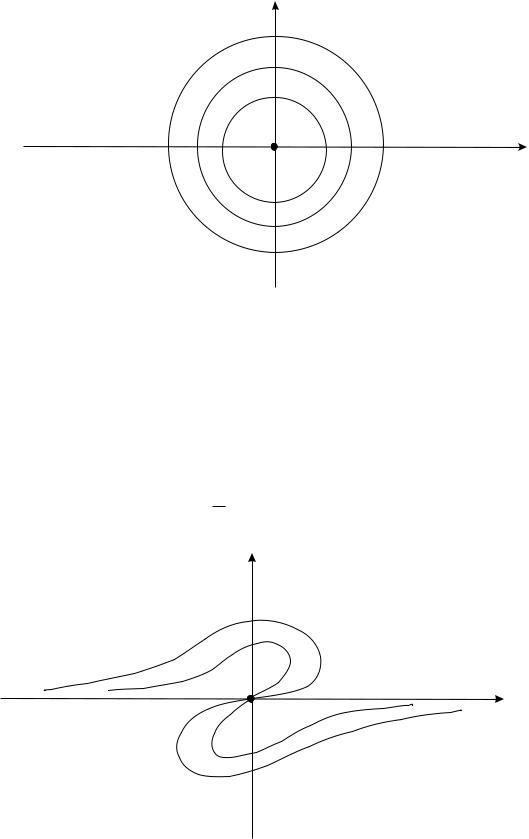
расположение траекторий называется фокусом. При α = 0, C1 ≠ 0 все траектории являются окружностями (рис. 39.4). В этом случае имеем центр. Отметим, что в случае центра
все траектории являются периодическими с периодом 2βπ.
182
Y2
O |
Y1 |
Рис. 39.4.
4. Собственные числа λ1 = λ2 = λ, а вещественная
нормальная форма Жордана J = ( |
λ 1 |
0 λ ). В этом слу- |
чае траектории дифференциальной системы (39.3) расположены на кривых (У–32)
1
y1 = λy2(ln|y2| + C), y2 = 0.
Y2
O |
Y1 |
Рис. 39.5.
Картина расположения траекторий носит название вырож-
183
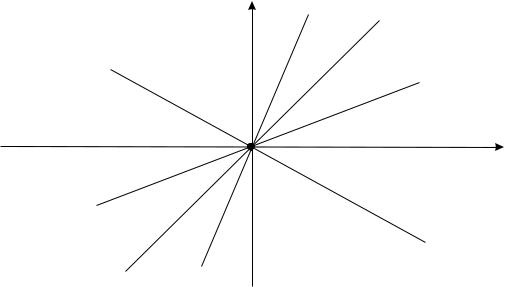
денный (монокритический) узел (см. рис. 39.5).
5. Собственные числа λ = λ = λ, а вещественная
1 2 ( )
λ 0
нормальная форма Жордана J = . Траектории
0 λ
дифференциальной системы (39.1) расположены на прямых
y1 = Cy2, y2 = 0.
Картина расположения траекторий называется дикритический узел (рис. 39.6).
Y2
O |
Y1 |
Рис. 39.6.
Изложенная в этом параграфе классификация принадлежит гениальному французскому математику Анри Пуанкаре (1854 – 1912).
Кроме того, отметим, что преобразование, которое было использовано при переходе от дифференциальной системы (39.2) к дифференциальной системе (39.3), есть аффинное преобразование плоскости, оставляющее неподвижным начало координат. Оно состоит в повороте на некоторый угол вокруг начала координат и в сжатии или растяжении относительно двух взаимно перпендикулярных осей. При этом прямые переходят в прямые, а окружности – в эллипсы.
184
Рассмотрим теперь дифференциальную систему |
|
||
|
dx |
= Ax + g(x), |
(39.4) |
|
dt |
||
|
|
|
|
где g(0) = 0, вектор–функция g аналитична в окрестности точки O, у разложений компонент этой функции в степенной ряд в окрестности этой точки отсутствуют линейные члены. Доказано, что при det A ≠ 0 и отсутствия чисто мнимых характеристических корней у матрицы A характер состояния равновесия O у дифференциальных систем (39.2) и (39.4) одинаков. При det A ≠ 0 и наличия чисто мнимых характеристических корней у матрицы A состояние равновесия O может быть центром или фокусом (т.е. возникает проблема различения центра и фокуса).
Плоскую линию J называют жордановой, если
J = {φ(t), α 6 t 6 β},
где функция φ : [α, β] → R2 непрерывна, φ(α) = φ(β), и
φ(t1) ≠ φ(t2), α 6 t1 < t2 6 β. Справедливы следующие утверждения.
Теорема 39.1 (Жордана). Если J есть плоская жорданова линия, то ее дополнение в плоскости состоит из объединения двух непересекающихся открытых множеств E1 и E2, причем границы ∂E1 = ∂E2 = J.
При этом одно из множеств Ek, k = 1, 2, ограничено и называется внутренностью линии J, а другое – внешностью линии J.
Теорема 39.2 (Пуанкаре–Бендиксона). Если положительная полутраектория l+ решения x (т.е. при t → +∞) содержится в компактном подмножестве области G и lx не содержит точек покоя, то множество lx является циклом.
185
Как мы рассматривали ранее, расположение траекторий решений линейных дифференциальных систем (39.2) на плоскости R2 определяется типом точки покоя. Значительно сложнее дело обстоит с нелинейными дифференциальными системами вида (39.1). Прежде всего усложняются возможные типы точек покоя. Помимо основных типов (узел, седло, фокус, центр), появляются так называемые сложные точки покоя, которые можно рассматривать как результат слияния точек покоя основных типов. Главная же особенность нелинейных дифференциальных систем состоит в том, что помимо точек покоя, структура семейства траекторий системы определяется расположением и характером некоторых специальных траекторий, среди которых основную роль играют различные циклы, составленные из траекторий, и прежде всего – предельные циклы. Если рассматривать дифференциальную систему (39.1) как поле скоростей переноса массы на плоскости R2, то (при равномерном начальном распределении массы по плоскости) с течением времени t масса сосредотачивается около устойчивых точек покоя и устойчивых предельных циклов.
В настоящее время в основе многих естественных и технических теорий (прежде всего – в основе радиофизики и электроники) лежит математическая теория колебаний, которая базируется на математических моделях колебательных контуров, представляющих собой дифференциальные системы вида (39.1) в случае свободных колебаний или неавтономные дифференциальные системы, содержащие периодические по t слагаемые, – в случае вынужденных колебаний. При этом устойчивый свободный колебательный режим с заданной частотой и амплитудой колебания осуществим только в нелинейной дифференциальной системе с предельным циклом.
186
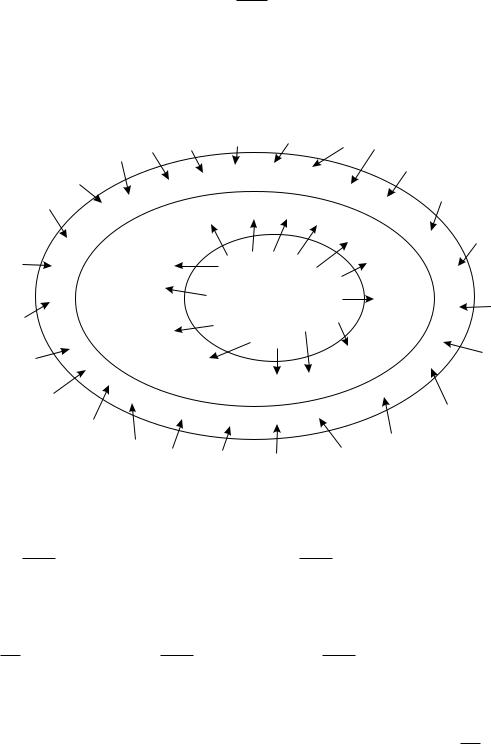
Одним из специальных приемов обнаружения предельного цикла является принцип кольца, предложенный Пуанкаре. Если удается построить кольцо K, ограниченное двумя гладкими кривыми Lk, k = 1, 2, такое, что на K нет точек покоя и все траектории пересекают Lk, входя (выходя из) K, то внутри K есть по крайней мере один предельный цикл (рис. 39.7). Этот принцип является непосредственным следствием теоремы 39.2 (Пуанкаре–Бендиксона).
L2
L1
Рис. 39.7.
Пример 39.1. Рассмотрим дифференциальную систему dxdt1 = x2 − x1(x21 + x22 − 1), dxdt2 = −x1 − x2(x21 + x22 − 1).
Для нее выполняется соотношение
dtd (x21+x22) = 2x1 dxdt1 +2x2(x21+x22)dxdt2 = −2(x21+x22)(x21+x22−1).
Поэтому окружность x21 + x22 = 1 является циклом исследуе-
d
мой дифференциальной системы. Выражение dt(x21 + x22) положительно на окружностях
L1 : x21 + x22 = r, 0 < r < 1,
187

и отрицательно на окружностях
L2 : x21 + x22 = r, r > 1.
Поэтому траектории входят в круговое кольцо, ограниченное окружностями L1 и L2. По принципу кольца наша дифференциальная система имеет предельный цикл – окружность x21 + x22 = 1. Этот предельный цикл устойчив (рис. 39.8).
Рис. 39.8.
При переходе к дифференциальным системам в Rn, n > 2, роль предельных циклов начинают играть предельные торы и более сложные геометрические поверхности. Задача исследования предельных торов аналитическими средствами существенно усложняется. Аналитический аппарат можно эффективно использовать лишь в отдельных случаях.
188
