45.Идеальные растворы. Закон Рауля. Закон Генри. Зависимость растворимости от температуры.

Идеальные расворы- растворы, у которых теплота растворения =0. Ясно, что в этих растворах характер взаимодействия м\у молекулами растворенного вещества и растворителя такой же, как и м\у молекулами растворителя. Это означает, что взаимодействие м\у молекулами в растворе не меняется, если заменить некоторое число молекул растворенного вещества на такое же число молекул растворителя, и наоборот. Давление насыщенных паров растворителя должно быть меньше их давления над чистым растворителем во столько же раз, во сколько плотность молекул растворителя меньше, чем когда он является чистым, без растворенного в нем вещества. Иначе говоря, давление насыщенных паров уменьшается во столько раз, во сколько уменьшается концентрация растворителя (закон Рауля): ,

где P1 – давление насыщенных паров растворителя над раствором; P1(0) – давление насыщенных паров над чистым растворителем; ν1 – количество молей растворителя; ν2 – количество молей растворенного вещества. Аналогично для давления насыщенных паров растворенного вещества получим: ,

где P2 – давление насыщенных паров растворенного вещества над раствором; P2(0) – давление насыщенных паров над чистым растворенным веществом. Закон Рауля справедлив для идеальных растворов. когда з-н характеризует относительную концентрацию вещества в растворе, если над раствором поддерживается давление P2 насыщенных паров этого вещества (закон Генри),то:

Из закона Генри следует, что для увеличения относительной концентрации растворенного вещества в растворе необходимо увеличить давление насыщенных паров растворенного вещества над растворителем; а для уменьшения концентрации – уменьшить давление.Отсюда следует, что при повышении Т растворимость веществ с положительной теплотой растворения убывает,а при понижении Т растворимость веществ с отрицательной теплотой растворения убывает, а с повышением Т возрастает.

46. Диаграмма состояния раствора. Кипение жидких растворов.

Рассмотрим диаграммы состояния жидких бинарных смесей при атмосферном давлении.

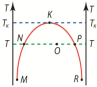
Данная диаграмма соответствует жидкостям, смешивающимся в произвольном количестве лишь при достаточно высокой Т. Линия MNK характеризует насыщенный раствор жидкости A в жидкости В а линия RPK соответствует насыщенному раствору жидкости B в жидкости A. При температуре T>Tк (критической температуры смешивания) жидкости A и B смешиваются в любых пропорциях. Область ниже кривой MNKPR – соответствует состоянию двухфазной системы с насыщенными растворами жидкости A в жидкости B, и жидкости B в жидкости A. Область, расположенная левее линии MNK, соответствует ненасыщенному раствору жидкости A в жидкости B. Область, расположенная правее линии RPK, соответствует ненасыщенному раствору жидкости B в жидкости A. Для характеристики состояния двухфазной системы действует правило рычага.Например, в состоянии характеризуемом точкой O, массы насыщенного раствора жидкости A в жидкости B (m_АВ) и раствора жидкости B в жидкости A (m_АВ) обратно пропорциональны длинам отрезков OP и ON:

Существуют диаграммы с двумя критическими температурами смешивания.

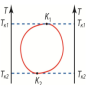Данная диаграмма соответствует жидкостям,смешивающимся в произвольном количестве лишь при достаточно высоких (T>Tк1) и достаточно низких

(T<Tк2) тем-х.Область ограниченная линией соответствует области двухфазных состояний, а сама линия соответствует насыщенным растворам.

47. Диаграмма состояния бинарных смесей. Осмотическое давление. Рассмотрим диаграммы состояния системы пар- жидкий раствор при постоянном атмосферном давлении. 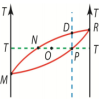Данная диаграмма соответствует бинарной смеси, компоненты которой смешиваются в любых пропорциях. Область, ограниченная замкнутой кривой MNDRPM, соответствует двухфазным состояниям, когда в объеме имеются одновременно и насыщенный пар и раствор. Ниже кривой MPR находится однофазное состояние, когда имеется только раствор. Область выше кривой MNDR соответствует однофазным состояниям системы в виде пара. В состоянии, которое соответствует точке P, имеется чистый раствор при температуре T, концентрация которого задается абсциссой этой точки (проекцией на горизонтальную ось). Точка M характеризует парообразное состояние при температуре T. Точка O определяет двухфазную систему. При этом, полная концентрация компонент в системе дается абсциссой этой точки, а массы жидкой и газообразной фаз относятся друг к другу обратно пропорционально длинам отрезков OP и ON.

Существуют и более сложные диаграммы состояния системы пар-жидкий раствор при атмосферном давлении.

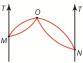Точка O характерна тем, что в ней состав жидкости и насыщенного пара одинаков. Кроме того, она соответствует состоянию, к которому придет кипящий раствор, если пары над ним удаляются. Разность давлений, которая возникает между областями, занятыми чистым растворителем и раствором, разделенными полупроницаемой перегородкой, называется осмотическим давлением. Осмотическое давление равно давлению разреженного газа этих молекул, т.е. может быть рассчитано по формуле для идеальных газов: , где ν -число молей молекул растворенного вещества в объеме V. Данное выражение называется законом Вант-Гоффа.