1. Модель материального тела. Атомы и молекулы. Взаимодействие молекул. Агрегатные состояния вещества. Модель идеального газа.

Молекулярной физикой называют раздел физики, занимающийся изучением зависимости физических свойств и агрегатных состояний тел от их внутреннего строения, сил взаимодействия между частицами, образующими тела, и характера их

движения. Все материальные тела состоят из мельчайших частиц, называемых молекулами. Поэтому моделью материального тела является совокупность атомов и молекул, взаимодействующих между собой по некоторым законам и соответствующим образом движущихся. Сами атомы и молекулы, входящие в материальные тела, могут быть представлены различными моделями в зависимости от обстоятельств и характера рассматриваемых явлений. В одних случаях можно считать их мат точками, в др – абсолютно твёрдыми материальными телами, в третьих необходимо принять во внимание их внутреннюю структуру и внутреннее движение. Поэтому моделью материального тела яв-ся совокупность атомов и молекул, св-ва, законы движения и взаимодействия которых известны. Модель идеального газа: 1)суммарный собственный объём всех молекул пренебрежимо мал по сравнению с объёмом сосуда; 2)м\у молекулами отсутствуют силы притяжения и отталкивания на расстоянии; 3)столкновение м\у молекулами газа и со стенками сосуда абсолютно упругие. В зависимости от взаимодействия молекул друг с другом материальные тела подразделяются на три агрегатных состояния: газ, жидкость, твердое тело. В газах молекулы настолько отдалены друг от друга, что практически не взаимодействуют между собой. Молекулы газа движутся от столкновения до столкновения со стенками сосуда или между собой равномерно и прямолинейно. Это движение хаотично. Давление, оказываемое газом на стенки сосуда, является следствием передачи импульса от движущихся молекул, при их соударении со стенками. В твердых кристаллических телах силы взаимодействия между молекулами очень велики и поэтому молекулы не могут удалиться друг от друга на большие расстояния. В результате совместного действия сил притяжения и отталкивания молекулы совершают колебания около некоторых средних положений, называемых узлами кристаллической решетки. Положению молекул в узлах кристаллической решетки соответствует минимальная энергия всего твердого тела. Любое изменение расстояния между молекулами в твердом теле требует приложения внешней силы. Молекулярное движение в жидкостях наиболее сложно. В нем наблюдаются черты, присущие тепловому движению частиц, как в газах, так и твердых телах. Каждая молекула в течение некоторого промежутка времени колеблется около определенного положения равновесия, которое само время от времени смещается на расстояние, соизмеримое с размерами молекул. В результате молекулы внутри жидкости колеблются и медленно перемещаются. Некоторое время они находятся около определенных мест, как бы в оседлом состоянии. Макроскопическая система: В классической физике предполагают, что молекулы движутся в соответствии с законами ньютоновской механики. Однако число молекул в любом теле очень велико: при обычных давлениях и температурах в каждом кубическом метре газа содержится порядка 10²⁵ молекул, а в жидких и твердых телах - порядка 10²⁸ молекул. Поэтому практически невозможно решить систему уравнений для описания движения молекул и найти вид траектории, а также закономерность движения по ней для каждой отдельной молекулы. Именно потому и говорят, что местоположение и скорость каждой молекулы изменяются во времени

случайным образом. Методы описания макроскопических систем: Для изучения физических свойств макроскопических систем, состоящих из очень большого числа молекул, используют два взаимно дополняющих друг друга метода: статистический и термодинамический. Статистический метод: метод основан на законах теории вероятностей и математической статистики. В совокупном движении огромного числа молекул, координаты и скорости которых в любой момент времени случайны,

проявляются статистические (вероятностные) закономерности. Раздел теоретической физики, в котором изучают физические свойства макроскопических систем с помощью статистического метода, называется статистической физикой. Термодинамический метод состоит в изучении физических свойств макроскопических систем путем анализа условий и количественных соотношений для процессов превращения энергии в рассматриваемых системах. Соответствующий раздел теоретической физики называют термодинамикой. Рассматриваемую макроскопическую систему в термодинамике называют термодинамической системой. Физические величины, служащие для характеристики состояния термодинамической системы, называют термодинамическими параметрами (параметрами состояния) системы. В качестве параметров состояния в термодинамике используют объем, давление, температуру и другие величины.

Идеальный газ - газ, в котором взаимодействие между молекулами происходит только путем их упругих столкновений между собой. Другие виды взаимодействия в таком газе отсутствуют. В реальном газе молекулы взаимодействуют друг с другом (притягиваются и отталкиваются). Любой реальный газ можно считать идеальным, если он достаточно разрежен. Рассмотрим равновесный газ, т.е. газ внутренние параметры которого зависят только от его внешних параметров и температуры. Равновесное состояние идеального газа (или любой простой системы) полностью определяется значениями всего лишь двух параметров - температуры Т и объема V (химический состав газа предполагается заданным). Соответственно, давление в такой системе . Это соотношение называют термическим уравнением состояния, или уравнением состояния, идеального газа. В термодинамике уравнение

состояния исследуемой системы предполагается известным из опыта. Законы идеальных газов: Закон Бойля-Мариотта: если Т, m=const, то Закон Гей-Люссака: если P, m = const, то Закон Шарля: если V, m = const, то Законы идеальных газов: Закон Дальтона: давление смеси газов равно сумме парциальных давлений каждого из газов, составляющих смесь. Закон Авогадро: один моль газа при нормальных условиях занимает объем равный 22,41 л.

Молем вещества называют такое его количество, в котором находится NA = 6,02∙10²³ молекул; NA - число Авогадро. Нормальные условия соответствуют температуре 273,15 градусов Кельвина (273,15 К) и давлению (1,013)·10⁵Па

Молярная масса = массе 1-го моля вещества. Обозначается M (не путать с m – массой газа). Количество молей ν = m/M = N/NA; N – число молекул в веществе. Уравнение состояния идеального газа Законы идеального газа можно свести к

одному уравнению (уравнению Менделеева-Клапейрона), где R=8,31 Дж/(моль·К) – универсальная газовая постоянная. Уравнение Менделеева-Клапейрона -допускает несколько различных форм записи: где n – концентрация молекул; k = R/NA = 1,38·10^-23Дж/К – постоянная Больцман

2. Основное уравнение кинетической теории газов. Основные газовые законы. Понятие температуры. Идеально-газовая шкала температур.

. Законы идеальных газов: Закон Бойля-Мариотта: если Т, m=const, то Закон Гей-Люссака: если P, m = const, то Закон Шарля: если V, m = const, то Законы идеальных газов: Закон Дальтона: давление смеси газов равно сумме парциальных давлений каждого из газов, составляющих смесь. Закон Авогадро: один моль газа при нормальных условиях занимает объем равный 22,41 л.

Молем вещества называют такое его количество, в котором находится NA = 6,02∙10²³ молекул; NA - число Авогадро. Нормальные условия соответствуют температуре 273,15 градусов Кельвина (273,15 К) и давлению (1,013)·10⁵Па

Молярная масса = массе 1-го моля вещества. Обозначается M (не путать с m – массой газа). Количество молей ν = m/M = N/NA; N – число молекул в веществе. Уравнение состояния идеального газа Законы идеального газа можно свести к

одному уравнению (уравнению Менделеева-Клапейрона), где R=8,31 Дж/(моль·К) – универсальная газовая постоянная. Уравнение Менделеева-Клапейрона -допускает несколько различных форм записи: где n – концентрация молекул; k = R/NA = 1,38·10^-23Дж/К – постоянная Больцмана.

Температура в молекулярной физике – мера хаотического движения молекул: чем больше температура, тем быстрее движутся молекулы. В термодинамике работают с абсолютной или термодинамической температурой, измеряемой по шкале Кельвина (K): T = 273,15 + t, где t – температура в градусах Цельсия. Например, 10 градусов Цельсия соответствует температура 283,15 К, а нулю градусов Цельсия – температура 273,15 К. Идеально-газовая шкала: Было замечено, что при постоянном объеме и массе идеального (т.е. реального разреженного) газа его давление зависит от температуры по закону где P₀-давление при начальной температуре. С помощью закона Шарля получим . Экспериментально измеренное α = 1/273,15 К^-1

Основное уравнение МКТ связывает давление с кинетической энергией молекул: ,где –масса одной молекулы, -средняя квадратичная скорость движения молекул, -средняя кинетическая энергия поступательного движения одной молекулы.

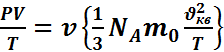Основное уравнение МКТ можно получить в следующем виде: , где N-число молекул в объёме сосуда V ; m0-масса одной молекулы; P-давление газа на стенки сосуда; - средняя квадратичная скорость движения молекул в газе. Основное уравнение МКТ можно преобразовать, если учесть, что имеем , или Пользуясь уравнением Менделеева-Клапейрона найдем 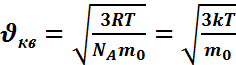,где k-постоянная Больцмана. С учетом того, что 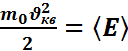- средняя кинетическая энергия движения молекулы, получим где i – число степеней свободы молекулы газа (для поступательного движения молекулы i=3). Из этого выражения следует, что на одну степень свободы приходится (1/2)kT энергии (теорема Больцмана). Таким образом, температура – мера средней кинетической энергии движения молекул газа.

3. Случайные величины. Частотное определение вероятности. Плотность вероятности. Теорема сложения вероятностей. Теорема умножения вероятностей. Случайная величина: В системе некоторых событий и некоторого (большого) числа факторов, определяющих реализацию событий, каждое событие имеет смысл случайного, если мы не можем точно определить факторы, приводящие к реализации данного события. Мерой реализации события служит его вероятность, т.е. то сколь часто событие реализуется. Например, если бросается игральная кость, имеющая 6 граней, то вероятность выпадения каждой из граней равна 1/6. Сумма всех вероятностей равна 1. Вероятность: Вероятностью i-го состояния w_i или вероятностью значения величины L_i называется предел отношения числа измерений N_i , дающих значение L_i , к полному числу измерений N, когда последнее неограниченно возрастает, т.е. . Вероятность i-го состояния w_i определяется также как предел t_i , в течении которого система находится в этом состоянии, к полному времени наблюдения T при неограниченном возрастании последнего: 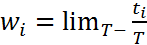. Условием нормировки вероятности является очевидное соотношение . Вместо того, чтобы рассматривать изменение состояния системы во времени, можно мысленно представить себе совокупность n систем, тождественных с данной, но в некоторый момент времени хаотически распределенных по всем возможным состояниям n_i. Такую систему называют статистическим ансамблем. Вероятность того, что при случайном измерении будет обнаружена система, находящаяся в i-м состоянии, равна Вероятность по ансамблю должна быть равна вероятности состояния. Это предположение называется эргодической гипотезой. Если состояния системы меняются не дискретным, а непрерывным образом, то определение рассмотренное ранее теряет смысл. Вместо него следует использовать 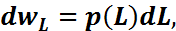где 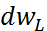–вероятность того, что величина L лежит в интервале м\у L и L+dL, p(L)- плотность вероятности. Условием нормировки вероятности является соотношение .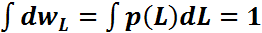

Теорема сложения вероятностей: Пусть одновременные нахождения системы в состояниях i и k являются взаимно исключающими друг друга событиями. Тогда время пребывания системы в одном из этих состояний, – безразлично в каком именно

(т.е. либо в i-м либо в k-м), - будет равна сумме времен пребывания в i-м и в k-м состояниях: – закон сложения вероятностей.

Теорема умножения вероятностей : Пусть имеются две совершенно независимые друг от друга системы. Обозначим и вероятности того, что первая система находится в состоянии и вторая система находится в состоянии . Вероятности и являются независимыми, если вероятность того, что первая система находится в состоянии i, не зависит от того, что вторая система находится в состоянии k. Тогда вероятность того, что одновременно первая система находятся в состоянии i, а вторая в состоянии k, равна – закон умножения вероятностей.

Tеорема умножения вероятностей: В самом деле, пусть мы следим за обеими

системами одновременно. Первая система проводит время в состоянии а вторая система из этого времени проводит время , в состоянии Искомая вероятность одновременного нахождения первой системы в состоянии , а второй в состоянии равна 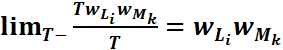, что и поясняет закон умножения вероятностей.

4. величин. Среднее по ансамблю и среднее по времени. Эргодическая Среднее значение дискретной и непрерывной случайных гипотеза.

Среднее значение зависит от переменной, по которой производится усреднение. Дискретная величина: - среднее значение; -квадрат среднего квадратичного значения; - условие нормировки. Полезные соотношения ;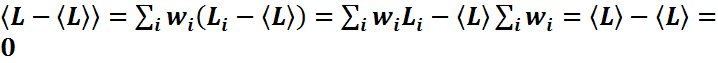

.

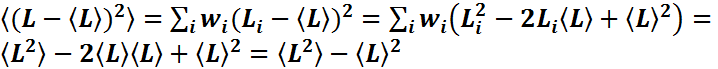Непрерывная величина: - среднее значение; - квадрат среднего квадратичного значения; - условие нормировки. Полезные соотношения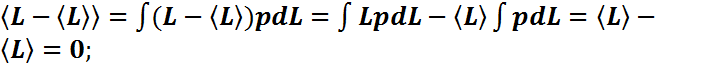

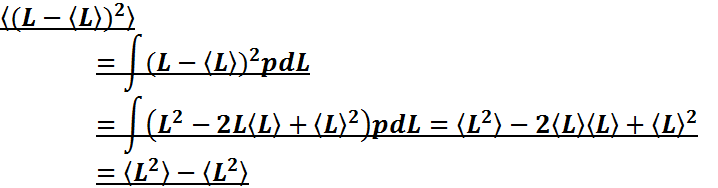
Вычисление средних по ансамблю: возьмём некоторую величину, связанную с конкретной частицей, например квадрат ее координаты. Расположение системы координат может быть произвольным, необходимо лишь, чтобы оно было одинаковым относительно всех систем ансамбля. Будем индексом i нумеровать координату частицы в i-й системе статического ансамбля. Тогда, по определению средней величины, получим: В этом равенстве индекс а показывает, что вычисляемая величина является средней по ансамблю, -число систем в ансамбле; -координата частицы в i-й системе ансамбля. Число ячеек в каждой системе ансамбля равно , а число систем в ансамбле предполагается значительно большим этой величины ()

Вычисление средних по времени: по определению ср по времени: ; i- последовательные скачки частицы; x_i – координата ячейки, в кот при своём движении частица переходит после i-го скачка, а -время пребывания частицы в этой ячейке после прибытия туда при i-м скачке. где m-число скачков в течении времени T. . При очень большом времени

за время Т она в j-й ячейке проведёт время где сумма берётся по всем i соответствующим j-й ячейке. Значит вероятность -продолжительность пребывания частицы в j-й ячейке относительно всего времени.

Эргодическая гипотеза. Утверждает что в состоянии равновесия средняя величина по ансамблю равна средней величине по времени.-наз эргодической гипотезой. Её можно выразить иначе: т.е. среднее по ансамблю равно ср по времени. Эргодическая гипотеза предполагает, что в этой совокупности имеются все возможные микросостояния системы, которые только совместимы с пространственными возможностями движения частиц и с законом сохранения энергии (если рассматриваются также и распределения частиц по импульсам). Любая из систем ансамбля в течении достаточно продолжительного промежутка времени пройдёт все возможные микросостояния, причём её относительное время пребывания в каждом из микросостояний равно относительному числу систем в ансамбле, нах в этом микросостоянии. Следствием является то что средние по ансамблю равны средним по времени.

5.Методы описания систем многих частиц. Микроскопическое состояние.Равновесное состояние.Статистический ансамбль систем.Системой называется конечная область пространства с находящимися в ней физическими объектами исследования. Граница системы может быть как материальной (например, стенка сосуда), так и воображаемой, проведенной в пространстве мысленно. Она может быть неподвижной или движущейся. Граница может быть проницаемой или непроницаемой для вещества, через нее либо невозможен, либо возможен транспорт энергии, причем в последнем случае она

классифицируется по формам энергии, которые через нее могут транспортироваться.

Система характеризуется не только особенностями своей границы, но и физическими или химическими свойствами вещества, находящегося в занимаемой системой области пространства. Классификация систем по этим признакам будет даваться

в книге по мере надобности. Первая система, с которой начинается рассмотрение, называется идеальным газом. Под идеальным газом понимается совокупность точечных частиц конечной массы, столкновение между которыми происходит по законам абсолютно упругого удара шаров, причем других способов взаимодействия

между частицами нет, т. е. силы взаимодействия на конечном расстоянии отсутствуют. Макроскопическое состояние. Пусть в некотором объеме V заключен идеальный газ. Предположим, что удары частицы о стенки сосуда абсолютно упругие, а масса сосуда очень велика, благодаря чему состояние движения из-за ударов частиц

по его стенкам не изменяется. Таким образом, заключенный в объеме V газ не

обменивается энергией с находящимися вне объема V материальными телами, т. е. является изолированным. При этом условии газ в сосуде изолирован от каких- либо внешних воздействий и все, что с ним может произойти, происходит

в результате внутренних причин.

По прошествии достаточного промежутка времени, в течение которого система предоставлена самой себе, состояние газа станет стационарным и не будет изменяться со временем. Состояние газа, характеризуемое его давлением, температурой и объемом, называется макроскопическим.

Равновесное состояние. Стационарное макроскопическое состояние газа, находящегося в изолированном от внешней среды объеме V, называется равновесным. При этом его макроскопические характеристики — давление, температура, объем — сохраняют свои постоянные значения во времени, причем давление и температура имеют постоянные значения во всех частях объема. Под частями объема имеют в виду достаточно большие части, в которых содержится очень большое число частиц. В определении равновесного состояния оговорка об изолированности системы

существенна. Если система не изолирована, то возможно стационарное состояние, которое не является равновесным. Если, например, различные части стенки сосуда,

в котором заключен газ, с помощью внешних источников теплаподдерживать при различной, но постоянной температуре, то в газе установится стационарное состояние, т. е. состояние, не изменяющееся со временем, однако оно не равновесное. В этом случае давление во всех частях объема одинаково, а температура во всех частях объема различна. Микроскопическое состояние. Наиболее полная информация о газе содержится

в констатации положений и скоростей всех его частиц Пронумеруем

частицы газа индексами i = 1, 2, ... п, т. е. всего в рассматриваемом объеме

имеется п частиц. Это число очень велико. Если объем L(3) = 1 см3, то при нормальных атмосферных условиях п = 2,7 -1019 частиц. Состояние газа, характеризуемое положениями и скоростями всех его частиц, называется микроскопическим. Следовательно, микроскопическое состояние газа характеризуется 6n числами: 3n

координатами (xi yi zi,) всех частиц и 3n компонентами (vxi vyi, vzi) их скоростей. Эти числа следует рассматривать как случайные величины. Макроскопическое состояние характеризуется тремя величинами: давлением, темпе-

ратурой и объемом, которые стационарном состоянии постоянны.

Однако частицы газа в стационарном состоянии движутся и, следовательно, его микроскопические состояния беспрерывно изменяются. Таким образом, одному и тому же макроскопическому состоянию соответствует громадное множество микроскопических состоянийСтатистический ансамбль систем. Метод ансамбля систем удобен для анализа вопросов статистической физики. Возьмем очень большое число N совершенно одинаковых сосудов, каждый из которых имеет объем V. В каждом из сосудов находится одинаковое число п одинаковых частиц. Сосуд с заключенными в нем

частицами называется статистической системой. Совокупность одинаковых статистических систем называется статистическим ансамблем.

Нас не интересует, как движутся частицы и в каких точках соответствующего сосуда они находятся в некоторый начальный момент времени. Задача заключается в том, чтобы изучить микро- и макросостояния отдельных систем ансамбля через некоторый достаточно большой промежуток времени, причем «достаточный промежуток времени» понимается в только что разъясненном смысле.

Из изложенного ясно, что одно и го же макроскопическое состояние осуществляется в большом числе систем ансамбля, находящихся в различных микроскопических состояниях..

6.Биноминальное распределение. Распределения Пуассона и Гаусса. Флуктуации.

Бином Ньютона выражается формулой Если p+q=1 и p, q>0, то бином Ньютона превращается в биноминальное распределение Биноминальное распределение соответствует распределению вероятности того, что при n испытаниях рассматриваемое событие (имеющее вероятность p) реализуется m раз. В случае больших n и m воспользуемся формулой Стирлинга, получим Дифференцируя это выражение по m и приравнивая к нулю, получим где m₀ – соответствует максимуму биноминального распределения.

Распределение Пуассона: В случае n>>m и np=m₀=const можно воспользоваться формулой Стирлинга 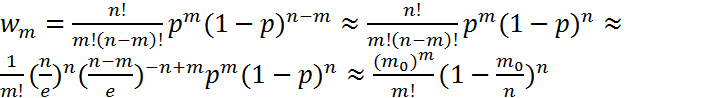В пределе получим - распределение Пуассона.

Распределение Гаусса: Прологарифмируем распределение Пуассона, получим или пользуясь формулой Стирлинга Разложим последнее выражение в ряд Тейлора

вблизи точки m=m₀, ограничиваясь квадратичным членом, получим 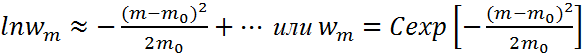, - называется распределением Гаусса.

Флуктуация: мерой флуктуации является стандартное отклонение от среднего значения. Роль флуктуации возрастает с уменьшением области, в которой эти флуктуации рассматриваются. В макроскопических системах статических флуктуаций незначительны. Относительная роль флуктуации уменьшается с увеличением области и среднего числа частиц в ней.

7.Распределение молекул по скоростям. Распределение Максвелла по вектору скорости. Распределение Максвелла по компонентам скорости. Скорости молекул в идеальном газе принимают произвольные значения. Скорость молекулы зависит от температуры. Распределение молекул по скоростям было

получено при следующих условиях: все молекулы имеют одинаковую температуру (газ равновесный); при соударениях молекул соблюдается условие детального

равновесия, т.е. при соударении пары молекул, когда эти молекулы поменяли свои скорости, в газе всегда найдутся две другие молекулы, которые приобрели те же самые скорости, которые имелись в первой паре до соударения, иначе, число молекул, имеющих заданную скорость не меняется со временем; все молекулы

одинаковые (имеют одинаковую массу и размер). Максвелл предположил, что число молекул газа, имеющих скорости в диапазоне равно Для нахождения нормировочного

коэффициента учтем, что 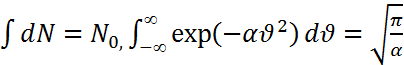. Распределение Максвелла по компонентам скорости имеет вид 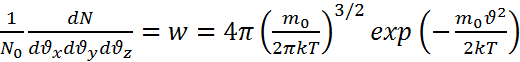, и распределение Максвелла по

абсолютному значению скорости имеет вид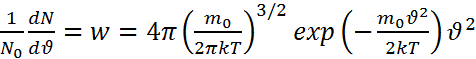

8.Распределение Максвелла по абсолютному значению скорости. Характерные скорости.

распределение Максвелла по абсолютному значению скорости имеет вид

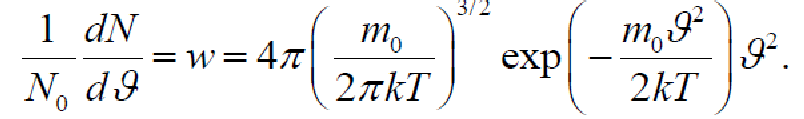
Характерные скорости

Средняя арифметическая скорость

Мы знаем среднюю квадратичную скорость. Вычислим среднюю арифметическую скорость по формуле

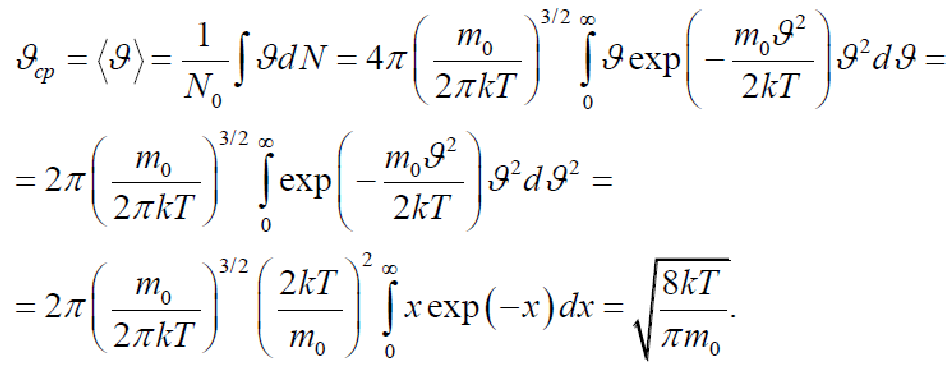
Нарисуем распределение Максвелла

Распределение Максвелла

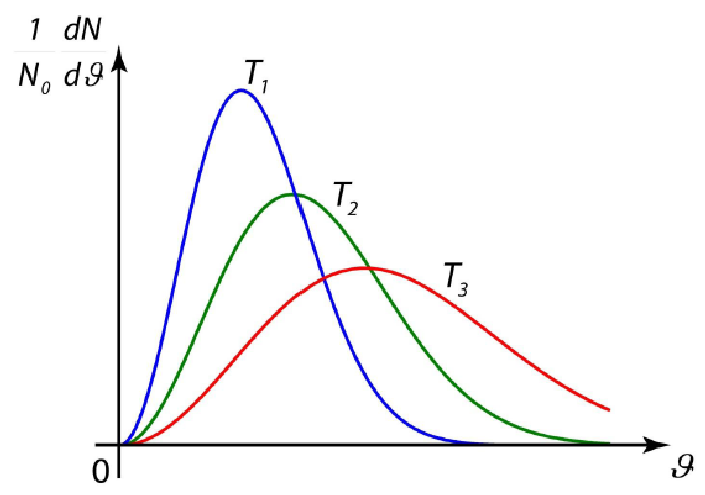
Наивероятнейшая скорость

Видно, что распределение Максвелла имеет максимум. Найдем соответствующую этому максимуму скорость, которая называется наивероятнейшей скоростью. Используем условие обращения в нуль производной в соответствующей точке. Имеем

9.Приведенное распределение Максвелла. Число молекул в различных участках распределения Максвелла. Принцип детального равновесия.

Приведенное распределение

Введем переменную

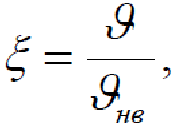Тогда распределение Максвелла примет т.н. приведенный вид

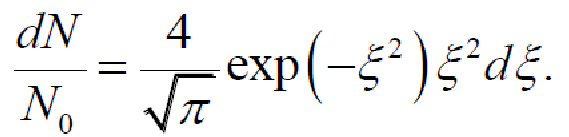
Число молекул, имеющих скорости в заданном интервале

Для нахождения числа молекул ΔN, имеющих скорости в диапазоне ϑ1<ϑ<ϑ2, следует найти интеграл

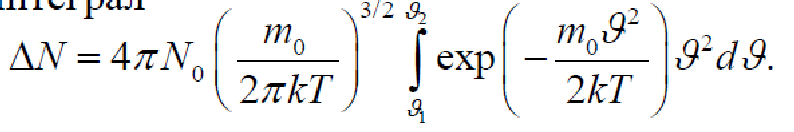
К сожалению, такой интеграл можно вычислить только численным способом. В случае скоростей из диапазона от ϑ до ϑ+Δϑ, где Δϑ<<ϑ, приближенно найдем

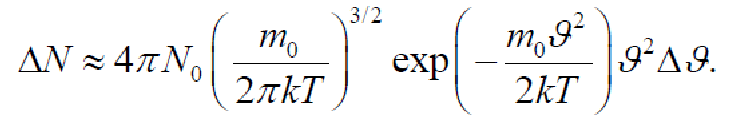
Численное вычисление дает

10.Число ударов молекул о стенку. Экспериментальная проверка распределения Максвелла. Границы применимости распределения Максвелла.

Экспериментальная проверка

Эксперимент Штерна 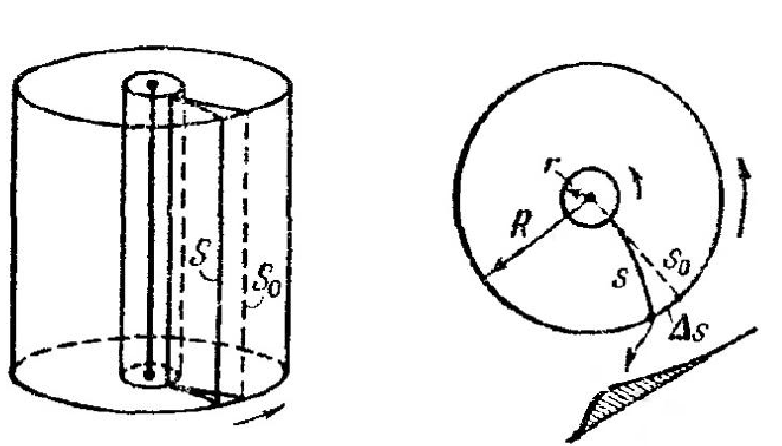Эксперимент Элдриджа

Частота ударов о стенку

Для нахождения частоты ударов молекул о стенку сосуда ν необходимо вычислить интеграл

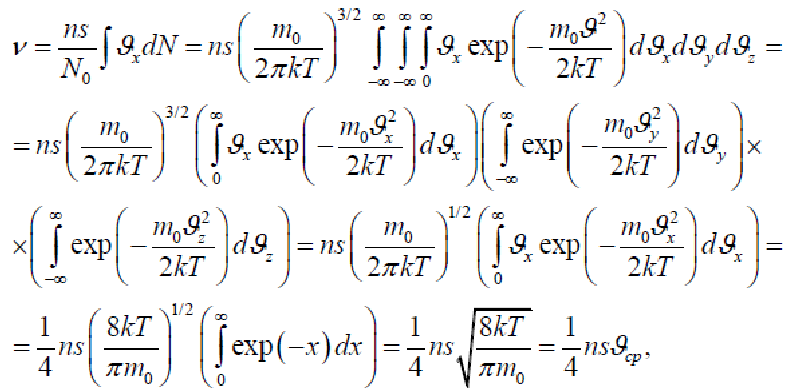
где n – концентрация молекул, s – площадь стенки. При вычислении было учтено, что вклад вносят только молекулы, движущиеся в направлении стенки (находящейся на положительной части оси x) и имеющих направление скорости нормальное, по отношению к стенке.

11.Поперечное сечение.Средняя длина свободного пробега.Частотоа столкновений.Экспериментальное определение длины свободного пробега молекул. Поперечное сечение. При движении в газе молекула испытывает столкновения, в результате чего она изменяет направление своего движения. Вероятность столкновения с конкретным результатом описывается с помощью понятия поперечного сечения. Пусть падающая частица попадает на площадь S объема, в котором расположены

частицы-мишени с концентрацией n0. В слое толщины dx находится число

частиц-мишеней n0Sdx, а сумма их поперечных сечений, которая как бы закрывает часть площади S, равна dS = n0S dx. Отсюда следует, что вероятность того, что падающая частица попадет в одну из частиц-мишеней в слое dx, равна1

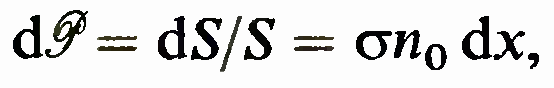где использовано определение вероятности. Это есть определение поперечного сечения а рассматриваемого процесса. Средняя длина свободного пробега. Величины и n0 не зависят, конечно, от х. Поэтому вероятность события растет пропорционально проходимому падающей частицей пути. Длина пути <l>, при которой эта вероятность равна единице, называется средней длиной свободного пробега. Для ее определения из1получается уравнение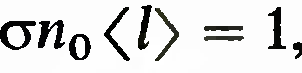 , из которого следует, что

Частота столкновений. Падающая частица движется со средней скоростью <v>> и, следовательно, проходит длину

среднего свободного пробега за время t= <l>/<v>. Поэтому средняя частота столкновений (среднее число столкновений за 1 с) равна

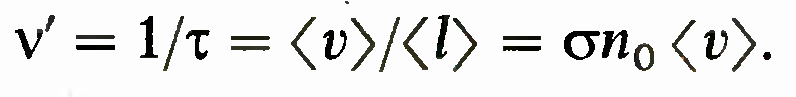
При рассмотрении столкновений одинаковых молекул в газах их чаще всего представляют в виде твердых шаров. Пусть молекулы-мишени неподвижны, а падающая на них молекула движется со скоростью <v>> . Очевидно, падающая молекула, пройдя расстояние х, столкнется со всеми молекулами-мишенями, центры которых находятся в круглом цилиндре с радиусом основания 2г0 и высотой х. Средняя длина свободного пробега равна

высоте цилиндра, в котором в среднем находится одна молекула-мишень. Поэтому для определения среднего

свободного пробега получаем уравнение

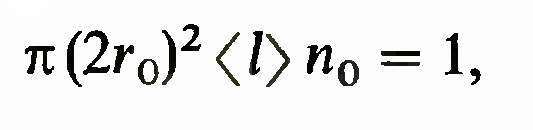
из которого следует, что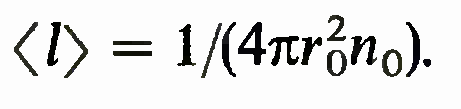

Частота соударений между молекулами на основании равна