
- •Вопросы к зачету для заочного отделения по курсу
- •II. Векторная алгебра.
- •III. Аналитическая геометрия.
- •IV. Математический анализ
- •I. Линейная алгебра Матрицы Прямоугольная таблица чисел
- •Пример. Даны матрицы а и в. ;. Найти произведение матриц ав.
- •Определители.
- •Методы решения систем линейных уравнений.
- •Обратная матрица.
- •Решение систем уравнений матричным методом.
- •Ранг матрицы.
- •Окаймляем его слева и снизу
- •Окаймляем d3 ( это только можно сделать двумя способами)
- •Прямоугольные системы уравнений.
- •Собственные векторы и собственные значения матрицы.
- •II. Векторная алгебра.
- •Единичным вектором, или ортом данного вектора, называется вектор, совпадающий по направлению с данным вектором и имеющий модуль, равный единице. Прямоугольные координаты
- •III. Аналитическая геометрия Аналитическая геометрия на плоскости
- •Если две прямые заданы уравнениями с угловым коэффициентом
- •Если уравнения прямых заданы в общем виде
- •Приведем уравнение прямой к нормальному виду. Нормирующий множитель
- •Аналитическая геометрия в пространстве
- •Уравнение плоскости в нормальном виде
- •Уравнение плоскости в отрезках на осях
- •Угол между двумя плоскостями
- •Острый угол между прямой иплоскостью
- •Кривые второго порядка.
- •Простейшее уравнение гиперболы
- •Асимптоты гиперболы - две прямые, определяемые уравнениями
- •Простейшее уравнение параболы
- •IV. Математический анализ Функция одной переменной
- •Предел функции.
- •Первый замечательный предел
- •Второй замечательный предел
- •Непрерывность функции
- •Дифференциальное исчисление. Производная. Техника дифференцирования. Обозначение
- •Производная сложной функции
- •Параметрически заданные функции и их дифференцирование
- •Правило Лопиталя
- •Применение дифференциального исчисления к исследованию функций
- •Признаки возрастания и убывания функций
- •Максимум и минимум функции
- •Первое достаточное условие существования экстремума функции
- •Второе достаточное условие существования экстремума
- •Асимптоты.
- •Общее исследование функции
Собственные векторы и собственные значения матрицы.
Характеристическим
уравнением матрицы А
=
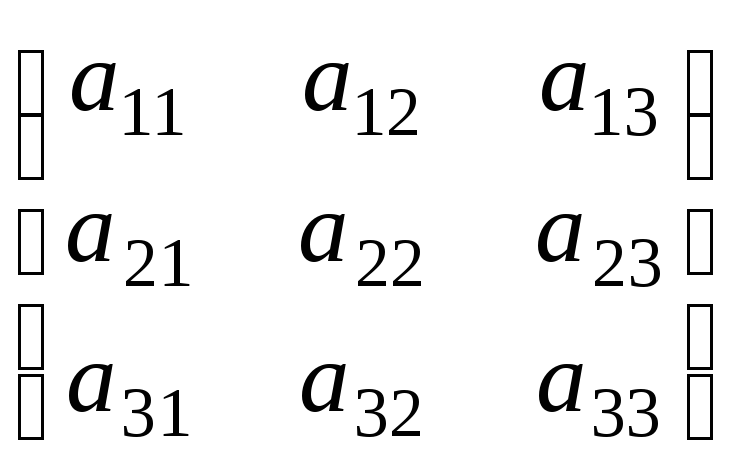 называется уравнение
называется уравнение![]() ,
т.е.
,
т.е.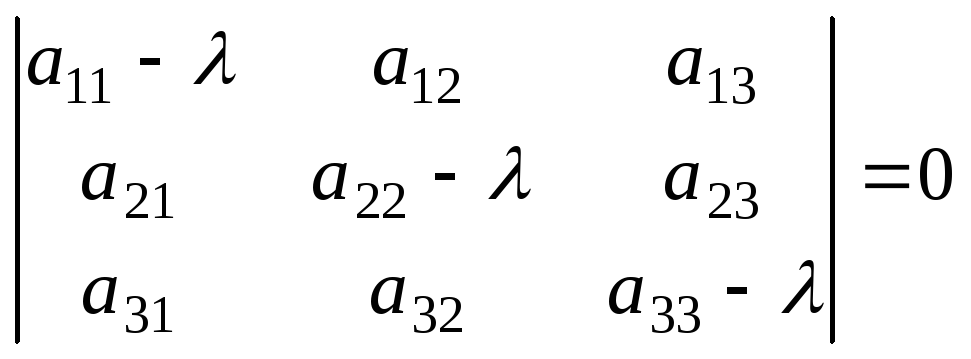 .
.
Корни этого уравнения 1, 2, 3 называются характеристическими числами матрицы А или собственными значениями матрицы А, эти числа действительные, если матрица является симметрической.Если элементы квадратной матрицы удовлетворяют условию аij = aji, то матрица называется симметрической.
Ненулевой
вектор х
называется
собственным
вектором квадратичной матрицы А,
принадлежащим ее собственному значению
совпадает с множеством всех ненулевых
решений системы однородных уравнений
(![]() )х
= 0, записанных в векторно-матричной
форме.
)х
= 0, записанных в векторно-матричной
форме.
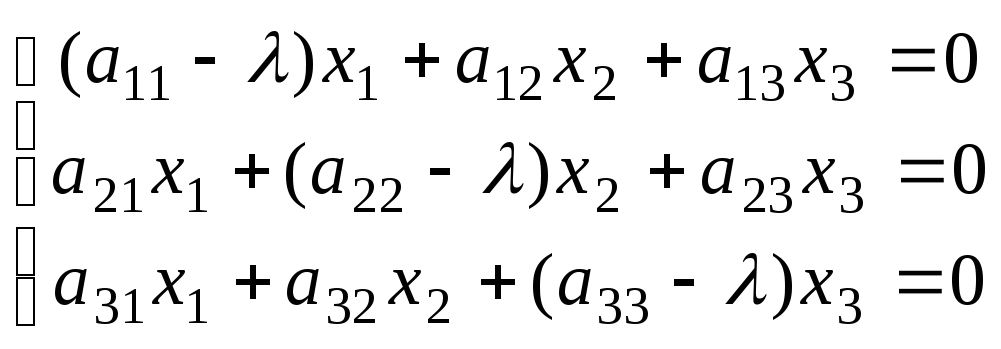
в
которой
имеет одно из значений 1,
2,
3
и определитель
которой в силу этого равен нулю, определяет
тройку чисел
![]() соответствующую данному собственному
значению который и является искомым
собственным вектором.
соответствующую данному собственному
значению который и является искомым
собственным вектором.
Пример.
Дана матрица
![]() .
Найти собственные значения и собственные
векторы.
.
Найти собственные значения и собственные
векторы.
Решение:
Составим
характеристическое уравнение
![]()
![]() =0
=0
(![]() )(
)(![]() )
– 8 = 0
)
– 8 = 0
2 - 8 + 7 = 0
1=7, 2 = 1.
Находим собственный вектор, соответствующий первому собственному значению
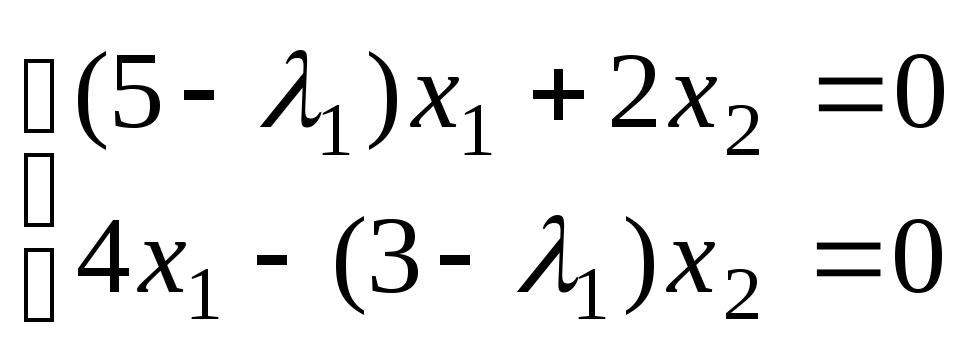 ;
;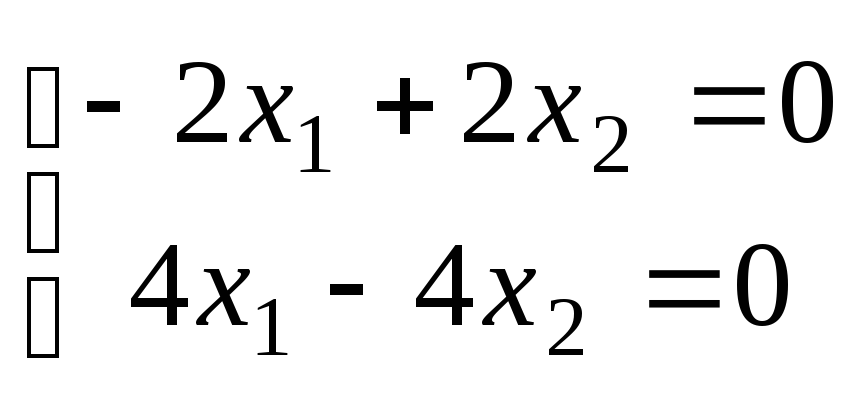
х1
= х2
х1
= х2
![]() - собственный вектор, соответствующий
собственному числу1=7
- собственный вектор, соответствующий
собственному числу1=7
Находим собственный вектор, соответствующий второму собственному значению
 ;
;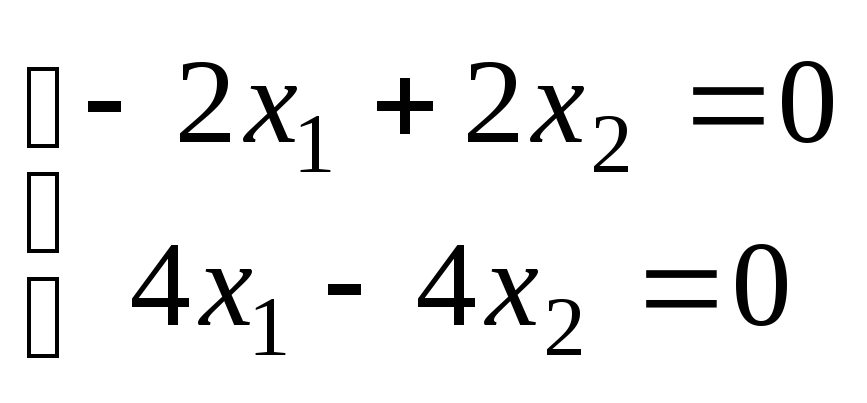
2х1
=- х2 х1
=
2х1
=- х2 х1
=![]() х2
х2
![]() - собственный вектор, соответствующий
собственному числу2
= 1
- собственный вектор, соответствующий
собственному числу2
= 1
II. Векторная алгебра.
Различают два рода величин: скалярные и векторные.
Если некоторая величина определяется только ее числовым значением, то ее называют скалярной. Если при определении некоторой величины для ее полной характеристики, кроме числового значения, надо знать и ее направление, то такая величина называется векторной, или вектором. Длина вектора называется также его модулем, или абсолютной величиной. Вектор равен нулю, если его модуль равен нулю. Такой вектор называется нулевым.
Два
вектора
![]() называются равными, если равны их
модули, они параллельны и сонаправлены.
называются равными, если равны их
модули, они параллельны и сонаправлены.
При
умножении вектора
![]() на
скаляр k
получается вектор
на
скаляр k
получается вектор![]() модуль которого равен модулю вектора
модуль которого равен модулю вектора
![]() ,
умноженному на k.
Направления
векторов
,
умноженному на k.
Направления
векторов
![]() совпадают,
если k
> 0, и они противоположны, если k
< 0.
совпадают,
если k
> 0, и они противоположны, если k
< 0.
Два вектора, лежащие на параллельных прямых называются коллинеарными.
Единичным вектором, или ортом данного вектора, называется вектор, совпадающий по направлению с данным вектором и имеющий модуль, равный единице. Прямоугольные координаты
Если в пространстве задана прямоугольная система координат Оxyz, то точка М пространства, имеющая координаты x (абсцисса), y (ордината), z (аппликата), обозначается М(x, y, z).
Расстояние
между двумя точками А(х1,
у1,
z1)
и В(х2
, у2,
z2)
определяется по формуле
![]() .
В частности, расстояние от точкиМ(x,
y,
z)
от начала координат О
определяется по формуле
.
В частности, расстояние от точкиМ(x,
y,
z)
от начала координат О
определяется по формуле
![]()
Если
х1,
у1,
z1-координаты
точки А,
а х2,
у2,
z2-
координаты точки В,
то координаты х
и
у точки С,
делящей отрезок АВ
в
отношении
![]() определяются
по формулам
определяются
по формулам
![]() ;
;
![]() ;
;![]()
Если λ == 1, то точка С(х, у,z) делит отрезок АВ пополам, и тогда координаты х и у средины отрезка А В определятся по формулам
![]() ;
;
![]() ;
;![]()
Площадь
треугольника на плоскости по известным
координатам его вершин А
(х1,
у1),
В(х2,
y2),
С (х3,
у3)
вычисляется по формуле .
.![]() Полученное
с помощью этой формулы число следует
взять по абсолютной величине. ЕслиS
= 0, то значит три точки лежат на одной
прямой.
Полученное
с помощью этой формулы число следует
взять по абсолютной величине. ЕслиS
= 0, то значит три точки лежат на одной
прямой.
Пример. Найти координаты точки С—средины отрезка, соединяющего точки
А (—2, 4) и В (—4, 10).
Решение.
В формулах![]() и
и
![]() возьмем
х1
= - 2; х2
= - 4;
возьмем
х1
= - 2; х2
= - 4;
у1=
4;
![]() =
10. Тогда абсцисса средины отрезкаАВ
х =-3; ордината
- у= 7.
=
10. Тогда абсцисса средины отрезкаАВ
х =-3; ордината
- у= 7.
Пример. Найти площадь треугольника, вершины которого находятся в точках А (2, - 3), В(1, 1), С(- 6, 5).
Решение: Задачу решим, воспользовавшись формулой площади треугольника
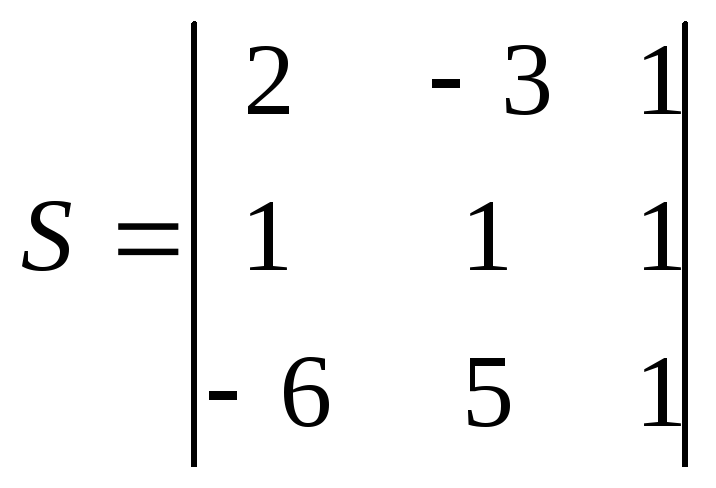 =
12
=
12
Ответ. S = 12 кв. ед.
Скалярное произведение.
Скалярным
произведением
двух векторов
![]() называется число, равное произведению
их модулей на косинус угла φ
между ними. Скалярное произведение
векторов
называется число, равное произведению
их модулей на косинус угла φ
между ними. Скалярное произведение
векторов
![]() обозначается символом
обозначается символом
![]() .
.
![]() =
=![]() cosφ.
cosφ.
Свойства скалярного произведения:
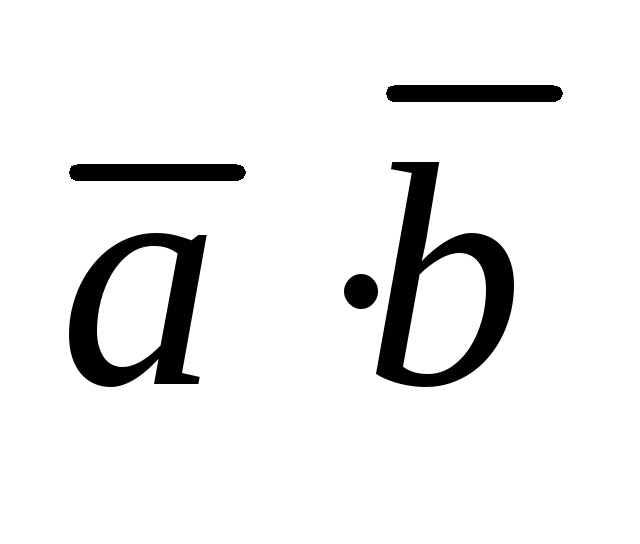 =
=
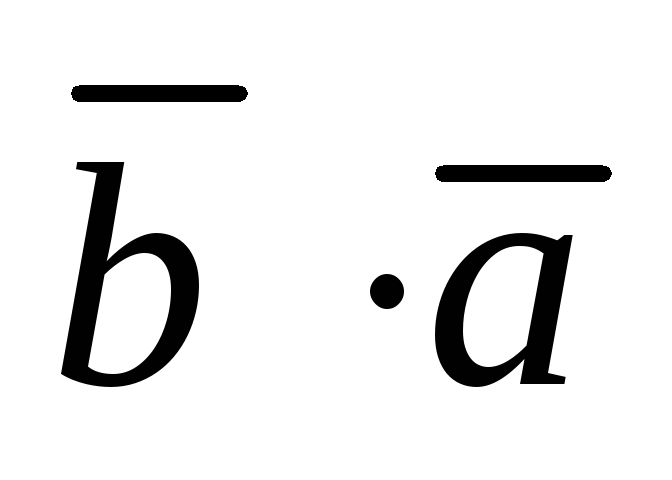 (переместительный
закон)
(переместительный
закон)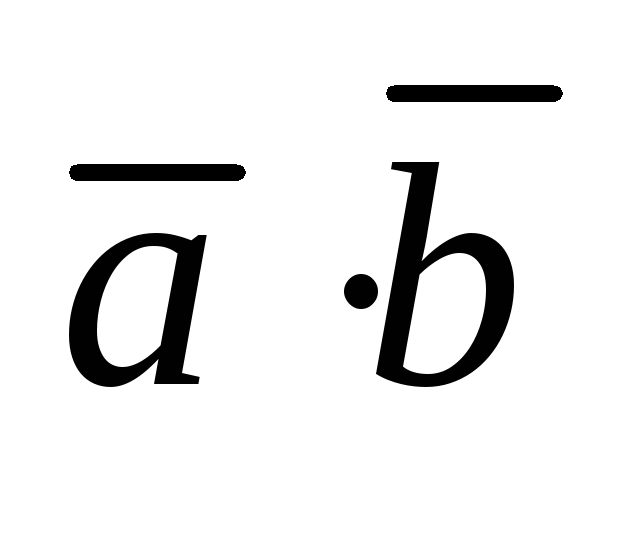 =
0, если
=
0, если
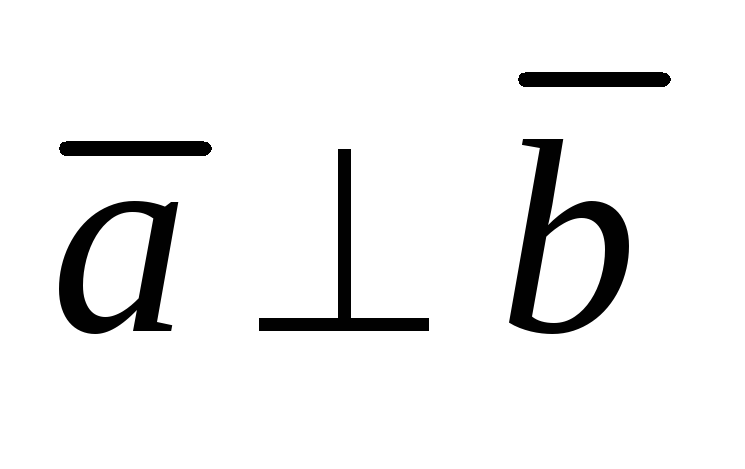 (скалярное произведение двух
перпендикулярных векторов равно нулю)
или какой-либо из перемножаемых векторов
является нулевым.
(скалярное произведение двух
перпендикулярных векторов равно нулю)
или какой-либо из перемножаемых векторов
является нулевым.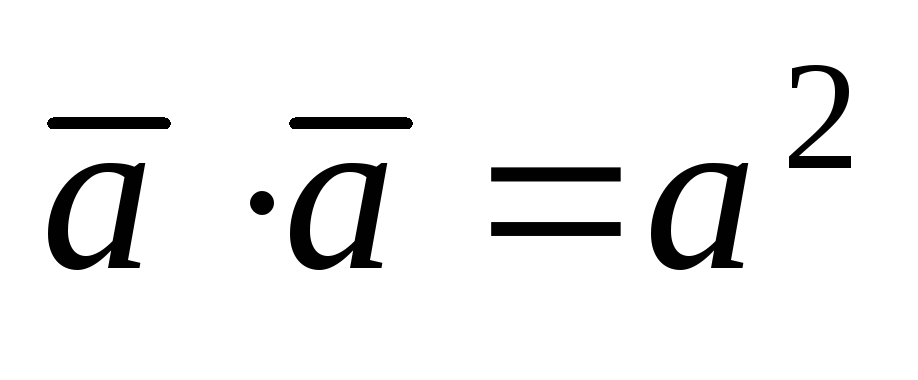
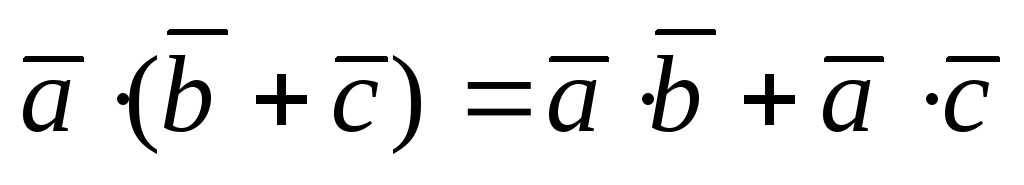 (распределительный
закон)
(распределительный
закон)
Скалярное
произведение ортов осей координат:![]()
Если
векторы
![]() заданы своими координатами:
заданы своими координатами:![]() ,
то их скалярное произведение вычисляется
по формуле
,
то их скалярное произведение вычисляется
по формуле
![]() =x1x2
+y1y2+z1z2.
=x1x2
+y1y2+z1z2.
Векторное произведение.
Векторным
произведением
векторов
![]() называется вектор
называется вектор
![]() ,
который определяется следующими
условиями:
,
который определяется следующими
условиями:
1)
Его модуль равен
![]() sinφ,где
φ
- угол между векторами
sinφ,где
φ
- угол между векторами![]() .
.
Модуль
вектора
![]() равен площади параллелограмма,
построенного на векторах
равен площади параллелограмма,
построенного на векторах
![]()
3)
![]()
![]()
Основные свойства векторного произведения:
1)
Векторное произведение
![]() равно
нулю, если векторы
равно
нулю, если векторы
![]() коллинеарны
или какой-либо из перемножаемых векторов
является нулевым.
коллинеарны
или какой-либо из перемножаемых векторов
является нулевым.
2)
При перестановке местами векторов
сомножителей векторное произведение
меняет знак на противоположный
![]() =
=![]() ;
;
3)(
![]() )
)![]() =
=![]() (распределительное свойство)
(распределительное свойство)
Если
векторы
![]() заданы своими координатами:
заданы своими координатами:![]() ,
то векторное произведение находим по
формуле:
,
то векторное произведение находим по
формуле:
![]() =
=
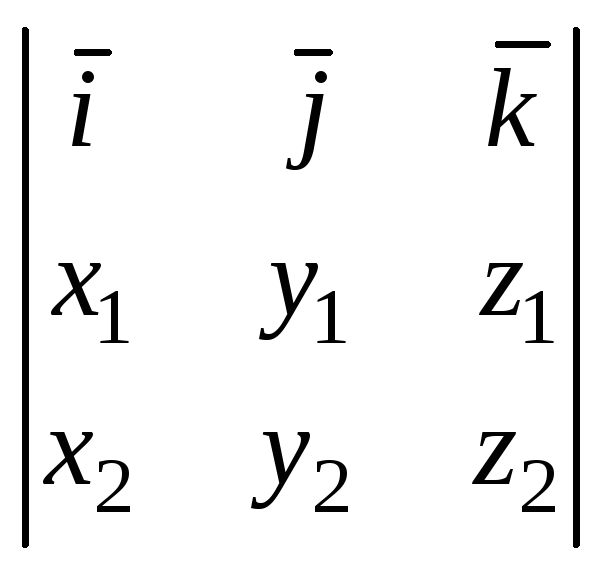
Площадь
параллелограмма и треугольника,
построенного на векторах
![]() ,соответственно
равны
,соответственно
равны
![]() ,
,![]()
Смешанное произведение
Векторно-скалярное
произведение трех векторов
![]() или смешанное
их произведение вычисляется по формуле
или смешанное
их произведение вычисляется по формуле
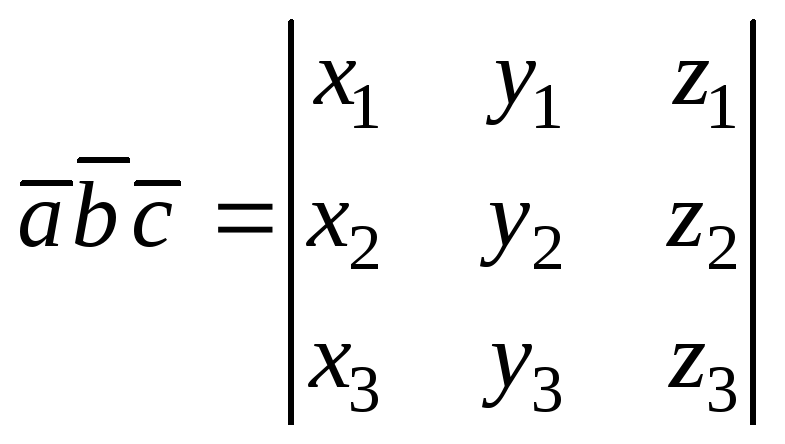 ,
если векторы
,
если векторы
![]() заданы своими координатами:
заданы своими координатами: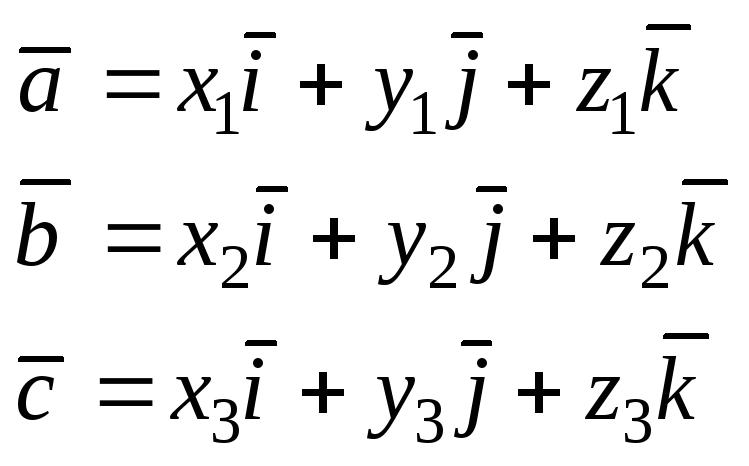 .
.
Абсолютная
величина смешанного произведения равна
объему параллелепипеда, построенного
на векторах
![]() .
.
Объем
пирамиды, построенной на векторах
![]() ,
получим по формуле
,
получим по формуле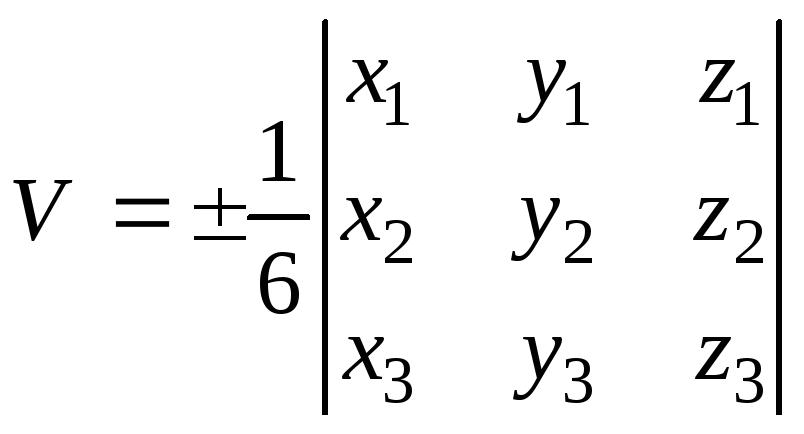 причем знак перед определителем должен
быть выбран так, чтобы объемV
был положительным.
причем знак перед определителем должен
быть выбран так, чтобы объемV
был положительным.
Три
вектора
![]() называются
компланарными, если они лежат в одной
плоскости или параллельны одной и той
же плоскости. Для того, чтобы три вектора
были компланарны, необходимо и
достаточно, чтобы их смешанное произведение
было равно нулю.
называются
компланарными, если они лежат в одной
плоскости или параллельны одной и той
же плоскости. Для того, чтобы три вектора
были компланарны, необходимо и
достаточно, чтобы их смешанное произведение
было равно нулю.
Пример. Начти объем пирамиды, если координаты ее вершин А(х1, у1, z1) и В(х2 , у2, z2)
Решение:
Рассмотрим векторы![]() ,на
которых построена пирамида.
,на
которых построена пирамида.
Зная координаты начала и конца каждого вектора, найдем проекции этих векторов на оси прямоугольной системы координат:
![]() ,
,![]() ,
,![]() для объема пирамиды получаем на основании
формулы
для объема пирамиды получаем на основании
формулы
