
- •Вопросы к зачету для заочного отделения по курсу
- •II. Векторная алгебра.
- •III. Аналитическая геометрия.
- •IV. Математический анализ
- •I. Линейная алгебра Матрицы Прямоугольная таблица чисел
- •Пример. Даны матрицы а и в. ;. Найти произведение матриц ав.
- •Определители.
- •Методы решения систем линейных уравнений.
- •Обратная матрица.
- •Решение систем уравнений матричным методом.
- •Ранг матрицы.
- •Окаймляем его слева и снизу
- •Окаймляем d3 ( это только можно сделать двумя способами)
- •Прямоугольные системы уравнений.
- •Собственные векторы и собственные значения матрицы.
- •II. Векторная алгебра.
- •Единичным вектором, или ортом данного вектора, называется вектор, совпадающий по направлению с данным вектором и имеющий модуль, равный единице. Прямоугольные координаты
- •III. Аналитическая геометрия Аналитическая геометрия на плоскости
- •Если две прямые заданы уравнениями с угловым коэффициентом
- •Если уравнения прямых заданы в общем виде
- •Приведем уравнение прямой к нормальному виду. Нормирующий множитель
- •Аналитическая геометрия в пространстве
- •Уравнение плоскости в нормальном виде
- •Уравнение плоскости в отрезках на осях
- •Угол между двумя плоскостями
- •Острый угол между прямой иплоскостью
- •Кривые второго порядка.
- •Простейшее уравнение гиперболы
- •Асимптоты гиперболы - две прямые, определяемые уравнениями
- •Простейшее уравнение параболы
- •IV. Математический анализ Функция одной переменной
- •Предел функции.
- •Первый замечательный предел
- •Второй замечательный предел
- •Непрерывность функции
- •Дифференциальное исчисление. Производная. Техника дифференцирования. Обозначение
- •Производная сложной функции
- •Параметрически заданные функции и их дифференцирование
- •Правило Лопиталя
- •Применение дифференциального исчисления к исследованию функций
- •Признаки возрастания и убывания функций
- •Максимум и минимум функции
- •Первое достаточное условие существования экстремума функции
- •Второе достаточное условие существования экстремума
- •Асимптоты.
- •Общее исследование функции
Методы решения систем линейных уравнений.
Решение
систем трех линейных уравнений с тремя
неизвестными x,y,z
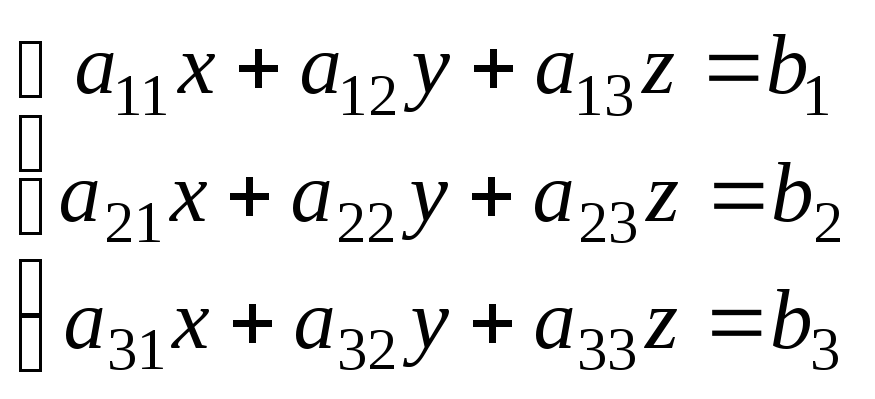
можно найти с помощью формул Крамера.
х
=
![]() ;y
=
;y
=![]() ;
z
=
;
z
=
![]() ,
,
где
D
=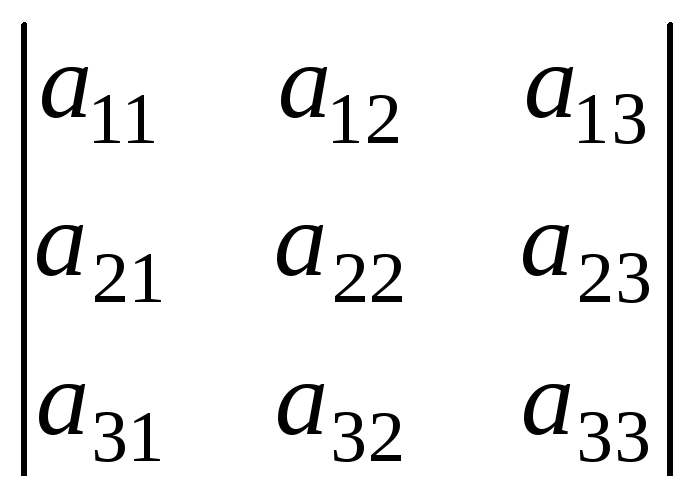 ,Dx
=
,Dx
=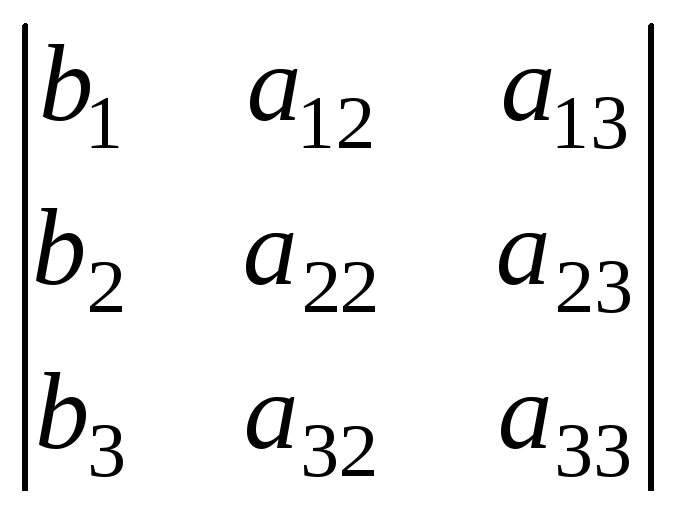 ;Dу=
;Dу=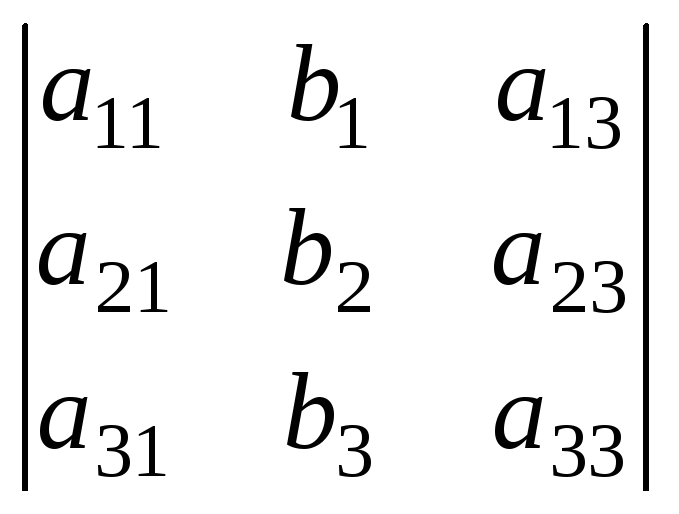 ;Dz=
;Dz=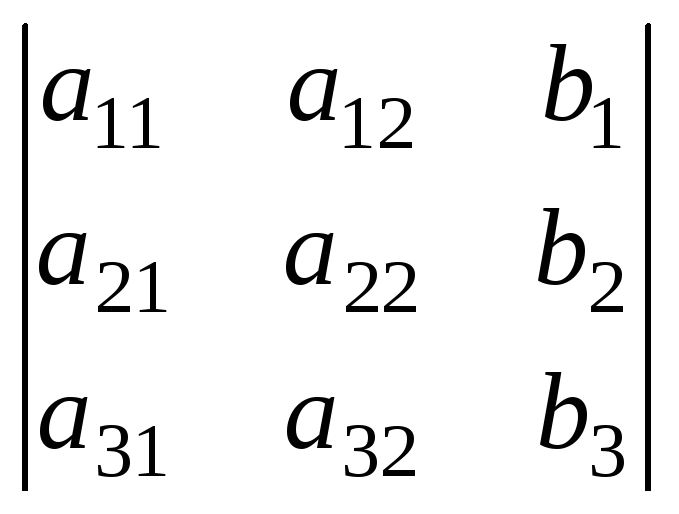 ,
,
При D 0 система имеет единственное решение. Если D = 0 ,то исходная система либо неопределенная, либо несовместная.
Пример. Решить систему линейных уравнений.
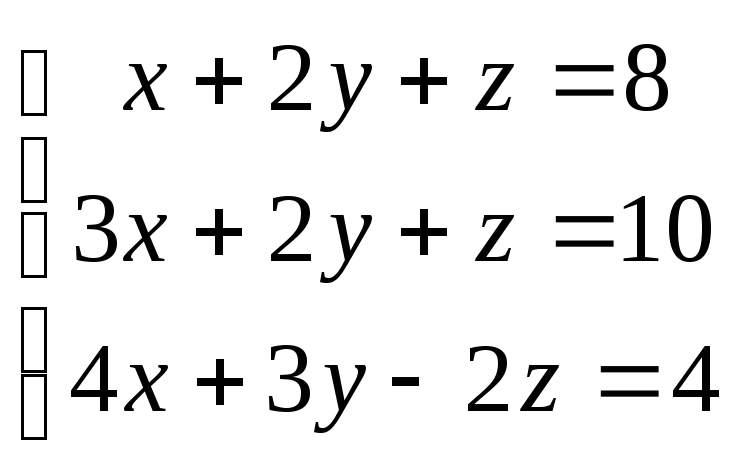
Решение:
D
=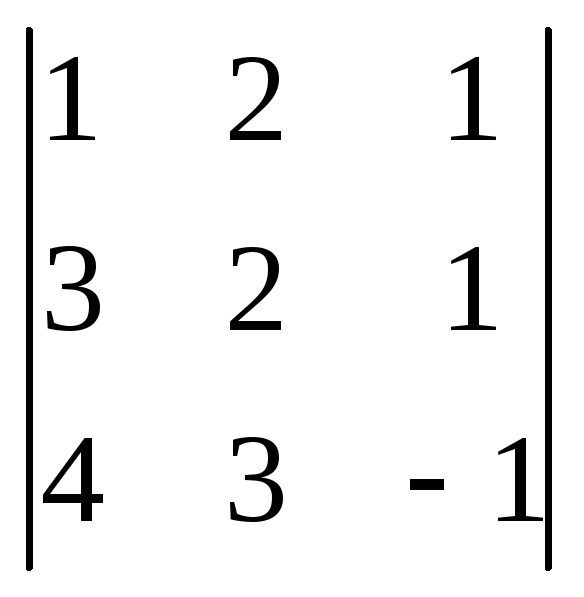 =14,
Dx=
=14,
Dx= =
14,
Dу
=
=
14,
Dу
= =28,
Dz
=
=28,
Dz
=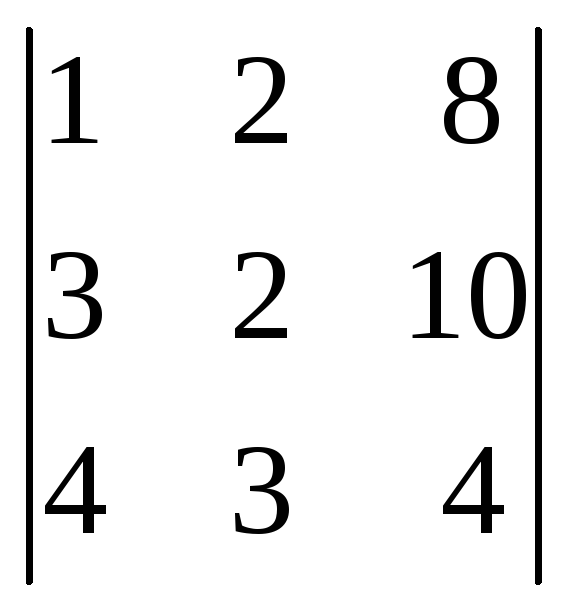 =42.
=42.
х
=
![]() =
=
![]() =1;
y
=
=1;
y
=![]() =
=![]() =
2;
z =
=
2;
z =
![]() =
=
![]() =3.
=3.
Метод Гаусса. Одним из способов решения линейных уравнений является метод Гаусса или метод последовательного исключения неизвестных. Этот метод заключается в преобразовании системы линейных уравнений к такому виду, где все элементы, лежащие по одну сторону от главной диагонали равны нулю. Удобнее приводить к ступенчатому виду не саму систему, а матрицу из коэффициентов и свободных членов. Переход от одной матрицы к другой будем осуществлять при помощи знака эквивалентности «~». Если система имеет единственное решение, то ступенчатая система уравнений приведется к треугольной, т.е. к такой, в которой последнее уравнение содержит одно неизвестное. В случае неопределенной – более одного неизвестного.
Общее решение строят из исходной системы уравнений с помощью элементарных преобразований, под которыми понимается любое из следующих действий:
1) вычеркивание уравнения, у которого все коэффициенты при неизвестных и свободный член равны нулю;
2) умножение обеих частей какого-либо уравнения системы на отличное от нуля число;
3) замена 1-го уравнения системы уравнением, которое получается путем прибавления к 1-му уравнению системы ее n-го уравнения, умноженного на число.
Пример. Решить систему уравнений методом Гаусса.
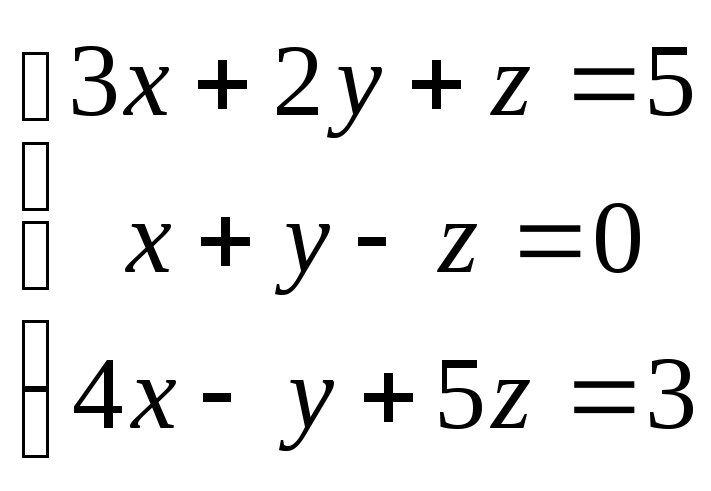 .
.
Решение:
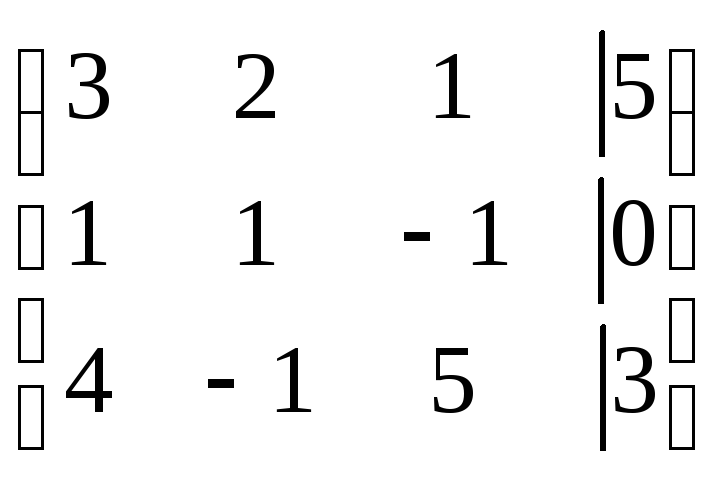 ~
~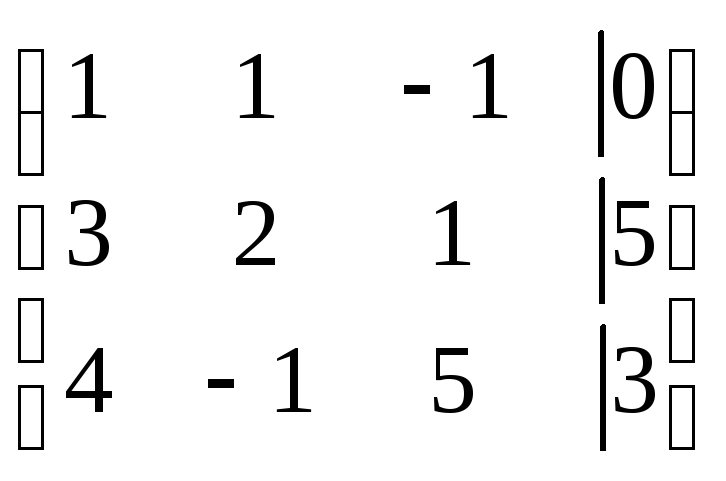 ~
~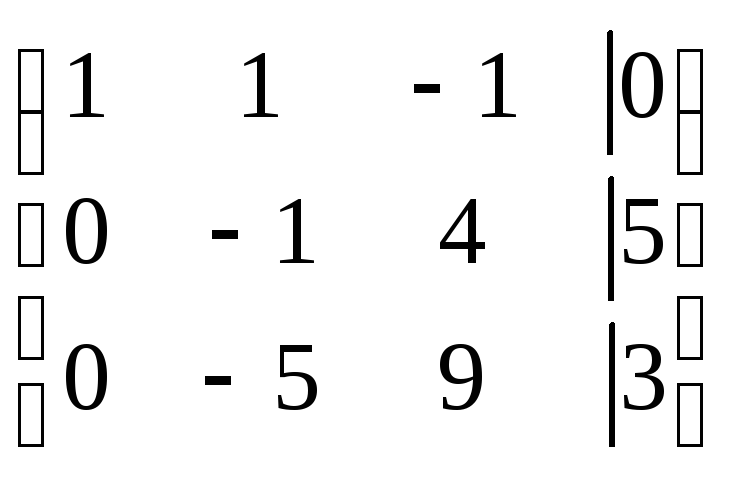 ~
~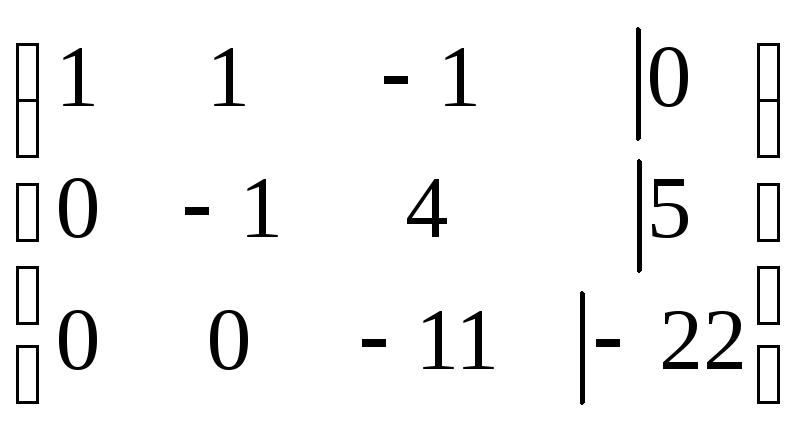 ~
~
Система приведена к треугольному виду. Запишем полученную систему:
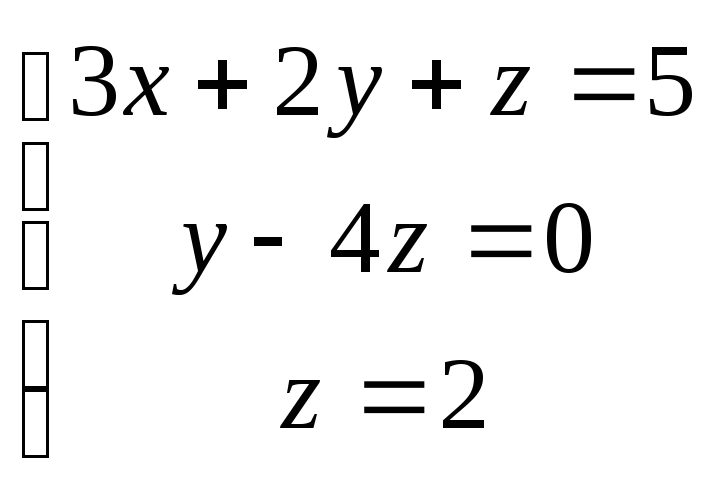
![]() .
.
Обратная матрица.
Обратной матрицей А-1 для матрицы А называется матрица, для которой выполняется равенство АА-1= А-1А=Е и которая имеет вид:
А-1
=
 .
.
Для того, чтобы найти обратную матрицу А-1 для матрицы А, нужно:
вычислить определитель матрицы А;
найти алгебраические дополнения ко всем элементам матрицы А;
записать обратную матрицу по формуле, обратив внимание, на то, что матрица, составленная из алгебраических дополнений транспонированна;
сделать проверку, перемножив данную и обратную матрицы. В результате должна получится единичная матрица.
Пример.
Дана матрица А=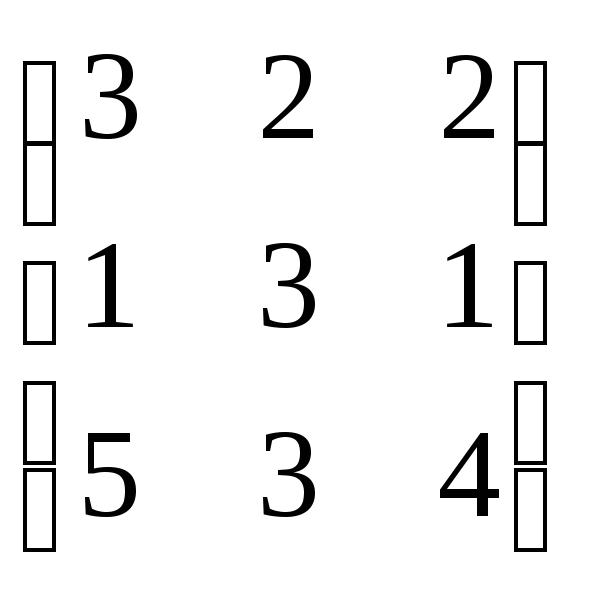 .
Найти обратную матрицу для данной.
.
Найти обратную матрицу для данной.
Решение:
Вычислим
определитель матрицы А.
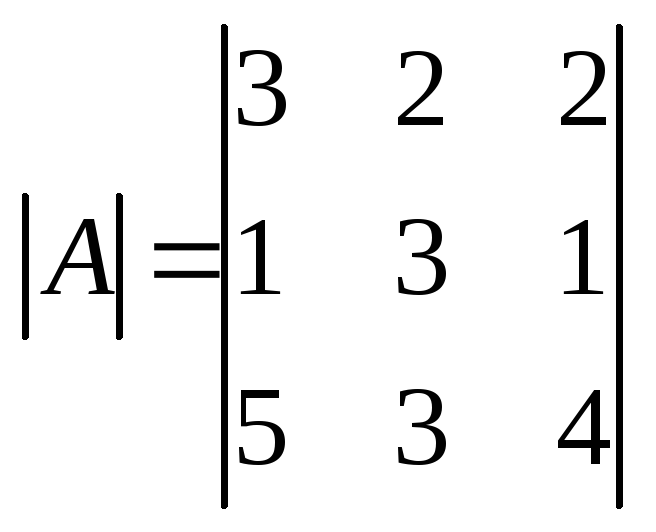 =
27 + 2 – 24 = 5.
=
27 + 2 – 24 = 5.
Найдем алгебраические дополнения:
![]() ;
;
![]() =
-2;
=
-2;![]() = 4
= 4
![]() = 1;
= 1;
![]() ;
;![]() = -1
= -1
![]() = -12;
= -12;
![]() = 1;
= 1;![]() = 7
= 7
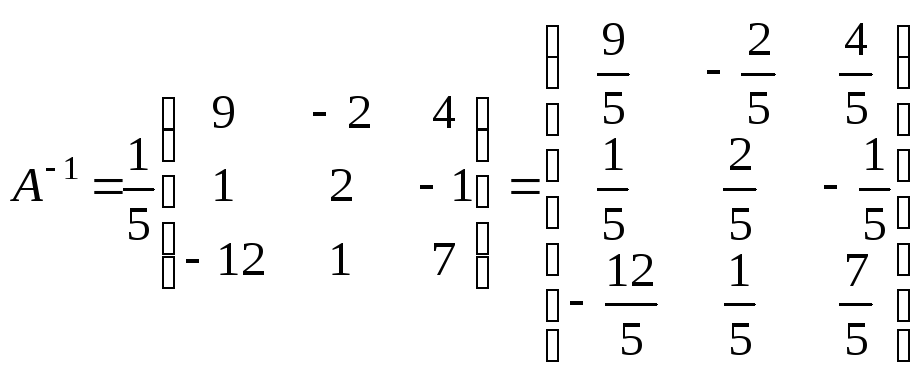
Решение систем уравнений матричным методом.
Система
уравнений
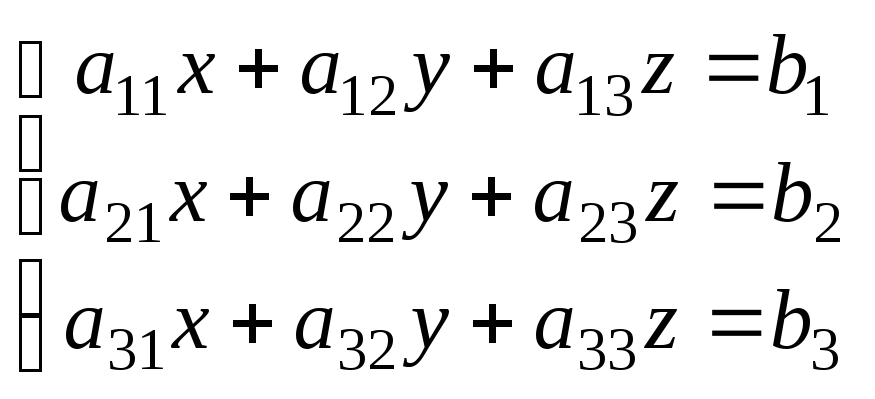 может быть записана в виде
может быть записана в виде
АХ
= В, где А
=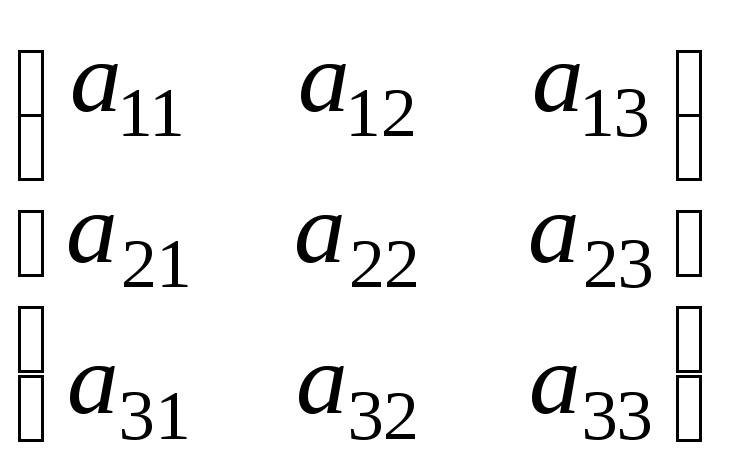 ,Х =
,Х =
![]() ,В =
,В =
![]() .
.
Решение
этой системы имеет вид: Х
=А-1
В (если
![]()
0).
0).
Пример.
Решить систему
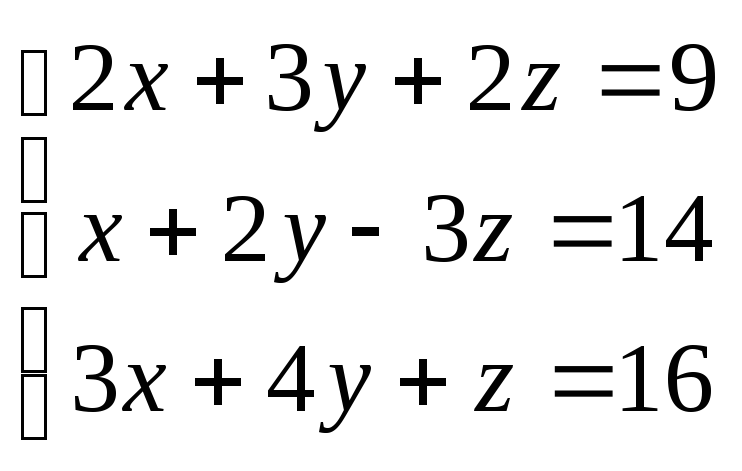 ,
представив ее в виде матричного уравнения.
,
представив ее в виде матричного уравнения.
Решение: Перепишем систему в виде АХ = В.
А
=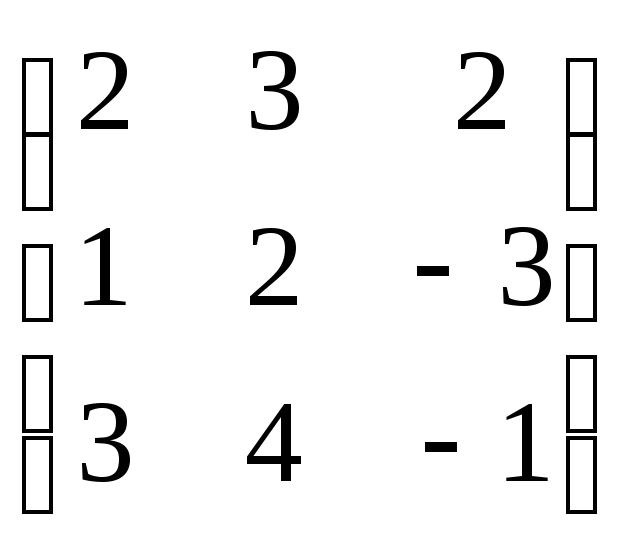 ,Х =
,Х =
![]() ,В =
,В =
![]() .
.
Решение матричного уравнения имеет вид: Х =А-1 В . Найдем А-1:
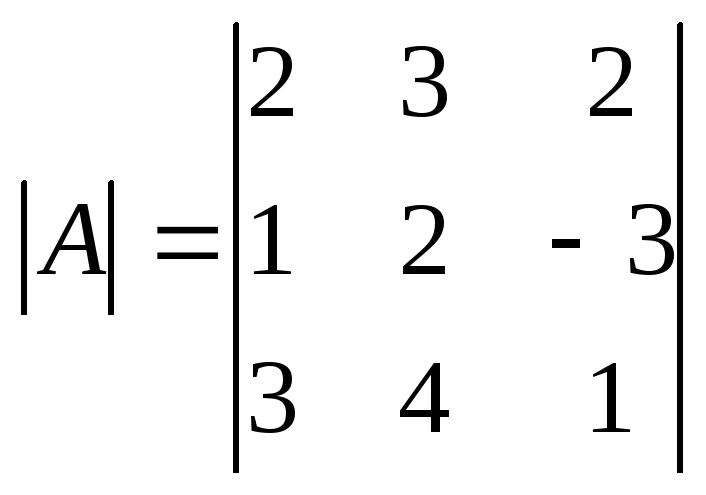 =
-6.
=
-6.
![]() ;
;
![]() =
5;
=
5;![]() = -13
= -13
![]() = -10;
= -10;
![]() ;
;![]() = 8
= 8
![]() = -2;
= -2;
![]() = 1;
= 1;![]() = 1
= 1
Откуда
Х
=
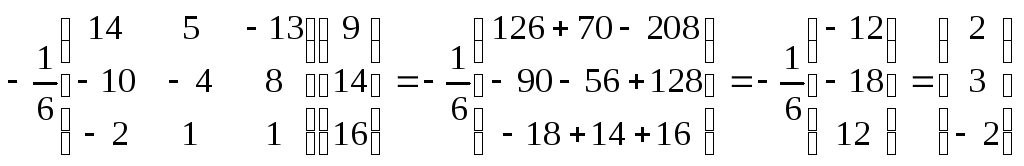 ,
,
следовательно, х = 2, y = 3, z = -2.
Ранг матрицы.
Дана прямоугольная матрица
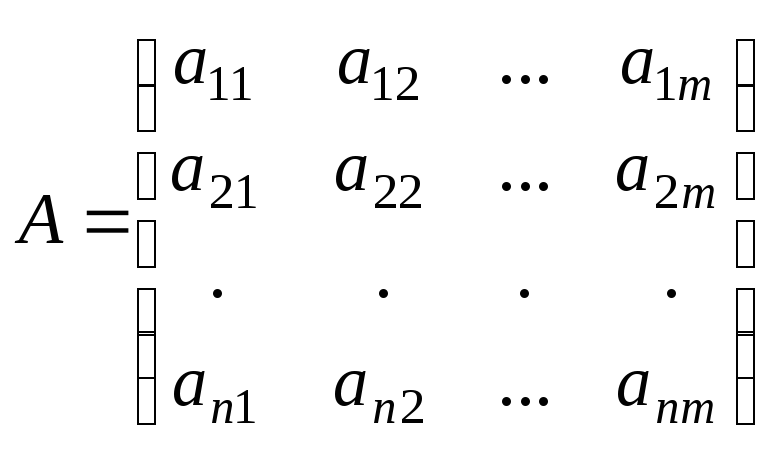
Выделим
в этой матрице k
произвольных строк и k
произвольных столбцов (k
![]() т,
т,
k
![]() n).
Определитель k-го
порядка, составленный из элементов
матрицы А,
расположенных на пересечении выделенных
строк и столбцов, называем минором
k-го порядка
матрицы А.
Рассмотрим всевозможные миноры матрицы
А. Рангом
матрицы А
называется
наибольший порядок минора этой матрицы,
отличный от нуля. Если все элементы
матрицы равны нулю, то ранг этой принимают
равным нулю.
n).
Определитель k-го
порядка, составленный из элементов
матрицы А,
расположенных на пересечении выделенных
строк и столбцов, называем минором
k-го порядка
матрицы А.
Рассмотрим всевозможные миноры матрицы
А. Рангом
матрицы А
называется
наибольший порядок минора этой матрицы,
отличный от нуля. Если все элементы
матрицы равны нулю, то ранг этой принимают
равным нулю.
Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы.
Ранг матрицы А будем обозначать через Dk (А). Если Dk (А)=Dk (В), то матрицы А и В называются эквивалентными. Ранг матрицы не изменяется от элементарных преобразований. Под элементарными преобразованиями понимают:
1) замену строк столбцами, а столбцов - соответствующими строками;
2) перестановку строк матрицы;
3) вычерчивание строки, все элементы которой равны нулю;
4) умножение какой-либо строки на число, отличное от нуля;
5) прибавление к элементам одной строки соответствующих элементов другой строки.
Пример.
Определить ранг матрицы:
 .
.
Решение: Все миноры второго и третьего порядков данной матрицы равны нулю, т.к. элементы строк этих миноров пропорциональны. Миноры же первого порядка (сами элементы матриц) отличен от нуля. Следовательно, ранг матрицы равен 1.
Практически удобно пользоваться следующим приемом: если найден минор k- го порядка Dk, то остается вычислить только те миноры (k+1)го порядка, которые представляют собой «окаймление» Dk.
Пример.
Определить
ранг матрицы: А
=
 .
.
D2
=
![]() ;
D2=
;
D2=
![]() .
.
