8.2 Перемещения при изгибе

Перемещения сечений балок характеризуется:

1) линейными перемещениями центров тяжести поперечных сечений в направлении, перпендикулярном геометрической оси балки z , которые называются прогибами .

2) угловыми перемещениями поперечных сечений вокруг нейтральной оси x, которые называются углами поворота сечений .

Уравнение, определяющие y и в произвольном сечении балки (рисунок 8.2):

Рисунок 8.2

(8.7)

(8.8)

Если равномерно распределенная нагрузка заканчивается не в конце балки, то эту нагрузку следует мысленно продолжить до конца и добавить противоположно направленную нагрузку такой же интенсивности (рисунок 6.2).

При этом в обобщенные уравнения углов поворота и прогибов, добавится ещё по слагаемому с противоположным знаком соответственно. Знаки слагаемых в обобщенных уравнениях устанавливают по правилу знаков для изгибающих моментов.

Положительное значение у обозначает прогиб вверх, и наоборот; положительное значение означает поворот сечения против часовой стрелки, и наоборот

Помимо расчетов на прочность балки нередко проверяют или рассчитывают на жесткость. Условие жесткости заключается в том, что максимальный прогиб (стрела прогиба f) или максимальный угол поворота не должно превышать допускаемых величин. Расчетные условия на жесткость имеет вид:

; (8.9)

8.3 Задание для ргр-6 по теме «Расчет балок на изгиб»

На (рисунке 8.3, 8.4приведены схемы балок требуется:

1. Для обеих схем построить эпюры изгибающих моментов и поперечных сил.

2. Руководствуясь эпюрой изгибающего момента, показать приблизительный вид изогнутой оси балки. По опасному сечению подобрать размеры поперечного сечения:

а) для схемы (рисунок 8.3а, 8.4а)

• прямоугольное h x в при

расчетом [τ] = 16 М Па (клееная древесина):h ·в= 1,5;

б) для схемы (рисунок 8.3б,

6.4б) – двутавровое (ГОСТ

8239-72) при расчетном

сопротивлении

[τ] = 200 М Па (сталь).

Данные взять из таблицы 9 Принять интенсивность равномерно распределенной нагрузки q = 6 кН/м.

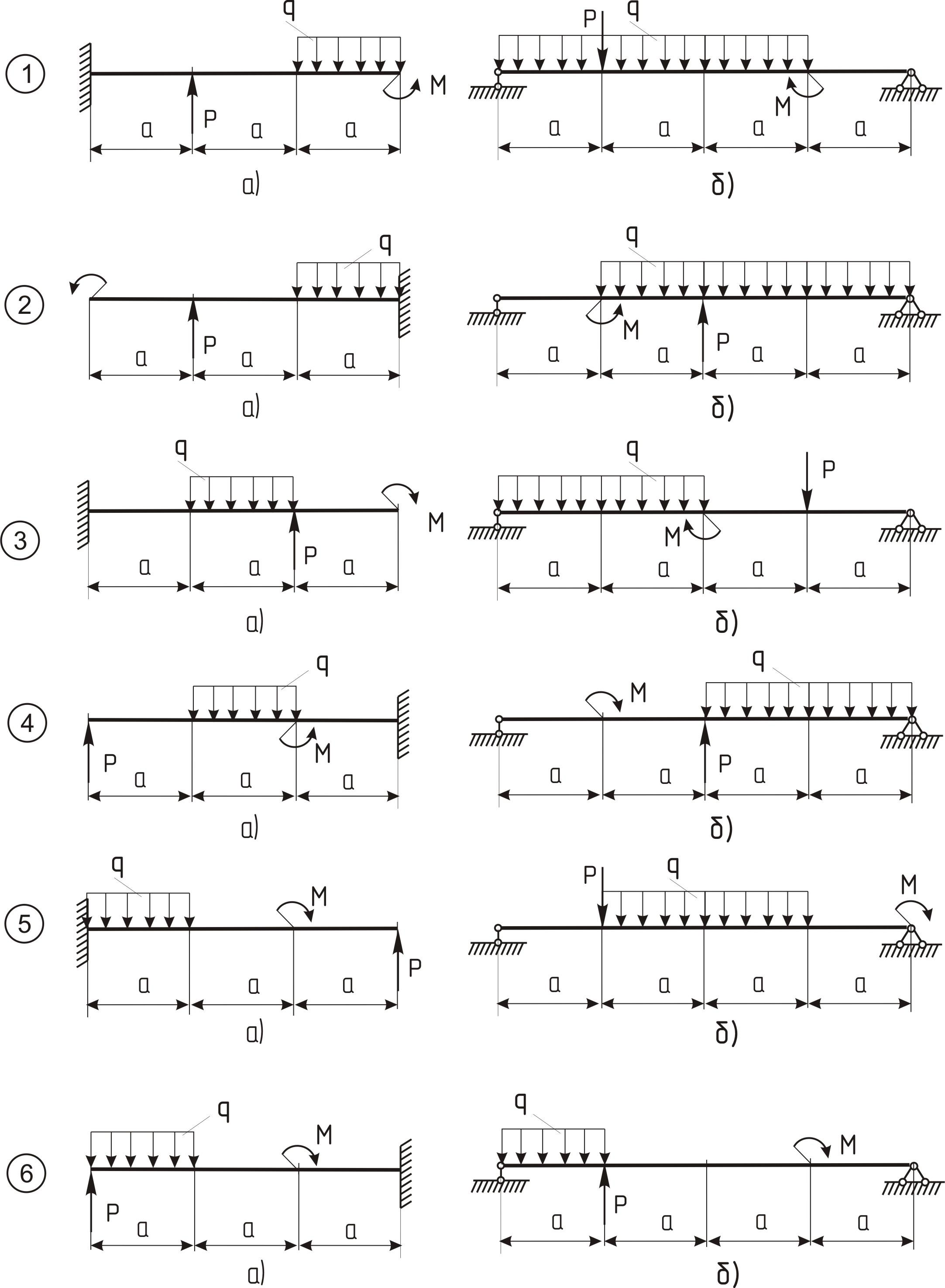
Рисунок 8.3

Рисунок 8.4

Таблица 9

№ схемы	а, м	Р, кН	М, кН · м
1	1,5	10	150
2	2,0	15	200
3	2,5	20	120
4	3,0	25	100
5	3,5	30	300
6	4,0	35	180
7	4,5	40	60
8	5,0	45	240
9	5,5	50	220
10	6,0	60	160

8.3.1 Пример решения РГР-6 на тему «Расчет балок на изгиб» (рисунок 8.5а).

Решение. Решение любой задачи в сопротивление материалов всегда надо начинать в определение опорных реакций. Однако, при построении эпюр внутренних силовых факторов Q и М, для заделанных одним концом балок (консолей) опорные реакции, возникающие в заделке (Н_А, R_А и М_А) можно не определять, так как они не войдут в уравнения равновесия правых отсеченных частей балки при расположении начало координат на свободном конце балки. Если же принять начало координат в заделке и при этом рассматривать равновесия левых отсеченных частей, то определение опорных реакций обязательно.

Для нашего примера начало координат примем в сечении D, т.е. на свободном конце балки. При этом отсчет координат z ведем от точки D влево.

1. Построение эпюр Q_у и М_х.

Для построения эпюр Q_у и М_х определяем количество участков, затем, используя метод сечений, составляем аналитические выражения изменения Q_у и М_х в зависимости от текущей абсциссы z для каждого участка.

Определение количество участков балки. Так как границы являются точки приложения нагрузок, то рассматриваемая балка (рисунок 6.5б) имеет три участка:участок I–DC, участокII–СВ, участокIII–ВА.

Рисунок 8.5

Составление аналитических выражений изменения Q_у и М_х и определение значений их в характерных сечениях каждого участка. Проведя сечение I-I, рассмотрим равновесия правой отсеченной части балки длиной z₁, приложив в ней все действующие справа от сечения заданной нагрузки и внутренние силовые факторы Q_у и М_х, возникающие в сечении, которые заменяют действие отброшенной части балки (рисунок 8.6). При этом предполагаем, что изображенные на рисунке внутренние силовые факторы положительны.

Рисунок 8.6 Рисунок 8.7

Составим уравнения равновесия Σ у = 0 и Σ для этой части балки и решив их, найдем аналитические выражения измененияQ_у и М_х в зависимости от z₁, на участке I, где z₁ изменяется в пределах 0 ≤ z₁ ≤ 1 м.

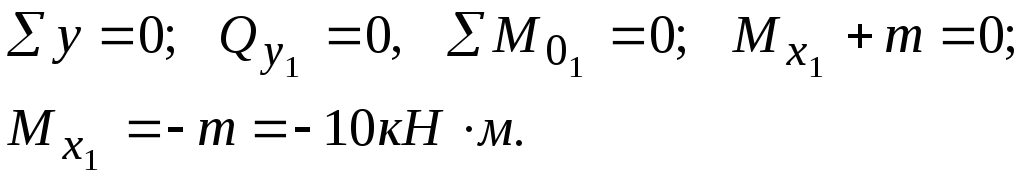
Полученные выражения показывают, что на участке I и - величины постоянные, так как не зависят от изменения z₁. Знак «минус» у , говорит о том, что момент в сечение I-I вызывает растяжение верхних волокон, что показано на рисунке 6.4. Участок II (1м ≤ z₂ ≤ 2м). Составим уравнения равновесия Σ у = 0 и для отсеченной сечением II-II правой части балки (рисунок 6.7) и определим и.

Σ у = 0;

Из полученных выражений для и видно, что на участке II величина постоянно, а величинаизменяется в зависимости отz₂ по закону прямой линии. Знак «минус» у показывает, что в сечении II-II возникает поперечная сила, действующая в обратном направлении показанному на рисунке 6.7 Теперь, подставляя значения z₂ для характерных сечений участка II в полученные аналитические выражения, определим величины и , возникающие в этих течениях, т.е. ординаты эпюр и в точках С и В.

При z₂= 1 м,

При z₂ = 2 м,

Участок III (2 м ≤ z₃ ≤ 4 м). Составим уравнения равновесия Σ у = 0 и Σ М₀ = 0 для отсеченной сечением III-III правой части балки (рисунок 6.8) и решив их, получим.

Рисунок 8.8

Таким образом, величина в пределах участкаIII изменяется по закону прямой линии, а величина по закону квадратной параболы в зависимости от величиныz₃.

Далее, подставим значения z₃, соответствующие характерным сечениям участка, в полученные аналитические выражения изменения и, определим ординаты этих эпюр для сеченийВ и А.

При z₃ = 2 м.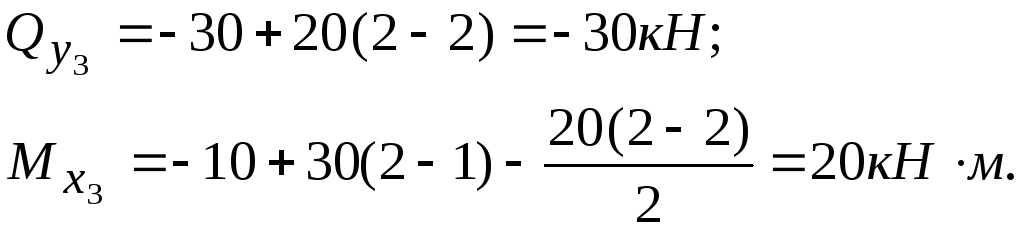

При z₃ = 4 м.

Так как поперечная сила в пределах участка меняет знак, т.е. имеет промежуточное нулевое значение (см. рисунок 6.5в), то в этом сечении возникает экстремальное значение изгибающего момента. Для определения его величины в начале найдем значение z₀, при котором

Подставим найденное значение z₀ = 3,5 м в аналитическое выражение изменения , вычислим величинуМ_тах.