
Геохімія
.pdf
181
|
C |
0 |
|
h x |
|
h x |
5.83 |
||||||
c(x,t) |
|
{erf |
|
|
|
erf |
|
|
|
} |
|
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
2 Dt |
|
2 Dt |
|
|||||||||
Приклад 5.6. Дифузія в кристалі
Вогненний кришталь є часто zonedas результат змін в складі магми. Допустіть olivine кришталь 2 mm діаметра з концентрацією 2000 ppm Ni раптом входить в контакті з магмою, в якій концентрація рівноваги повинна бути 500 ppm Ni. Як давно повинне це вважати за розповсюдження, щоб homogenize кришталь в температурі 1250° C, набуваючи миттєвого урівноваження в кришталевому рідкому кордоні?
Відповідь: Ми можемо поводитися з olivine кришталем, як сфера. Радіальна симетрія потім дозволяє нам розглянути проблему, як функція радіуса. Нам потрібно тільки розглядають зміну концентрації вздовж 1 радіального напряму з 0<x<r. Наша прикордонна умова, та в концентрації x = r (край кришталя) утримується постійним реакцією з рідиною. Ми повинні викликати цю концентрацію Cr. Початковий розподіл є c = Ci для 0 < x < r. Кривошип (1975)Accordingto, solutionis:
5.84
і концентрація в x = 0, C0, є:
5.85
Від рівняння 5.74, ми бачимо, що, як ухил концентрації зникає, розцінка розповсюдження іде до 0. Так кришталева однорідність підходів тільки asymptotically, стаючи однорідним тільки в t=, але це стане по суті однорідним більш швидко. Хороший шлях, щоб визначити “по суті однорідним" повинний - обгрунтувати це на нашій здатності виявити ухил. Якщо наша аналітична точність є тільки 5%, ми повинні мати багато трудності, яка виявляє ухил менше ніж 5%. Так що давайте повторно формулювати питання, щоб запитати, скільки часу вимагається перед тим, як різниця в концентрації між центром і оправою є менше ніж 5%? Ми встановлюємо C0/Cr=1.05 і в 5.84 і повторне впорядкування, ми одержуємо:
5.86
Оскільки це повертається зовні, для відносно великих значень t (Dt/r 2 > 0.1), підсумовування сходиться всередині 0.05% після першого строку, так, щоб 5.100 може був наближений:
2 (Ci/C r 1))
Для значення D=10-12 cm2/сухого, який дається Morioka і Nagasawa (1991), ми знаходимо, що близько 154 років вимагається перед тим, як olivine homogenizes. Якщо olivine, який витрачається менше, ніж цей час в контакті з магмою, ми повинні сподіватися, що це розділяється на зони в концентрації Ni. Фігура 5.14 показує те, як параметр Ni концентрації повинний помінятися з часом.
МАЛ. 5.14 - Розподіл Ni часом різний в сферичному olivine зерні з початковим замісником 2000 концентрації ppm і концентрації оправи, яка фіксується в 500 ppm.
Приклад 5.7.Урівноваження між Мінеральним Зерном і Водою Пори
Уявіть собі зерно calcite в осадку нагромадження, який оточується водним шляхом пори. Допускайте, що коефіцієнт Sr розподілу між calcite і водою є 100, що calcite має початкову концентрацію Sr 2000 ppm і, що постійна концентрація Sr 10ppm підтримується у воді, і, що зерно
181

182
сферичне. Якщо коефіцієнт розповсюдження для Sr в calcite є сухий 10-15 cm2 /і радіус calcite зерна є 1 mm, як є середню концентрацію Sr в зерновій зміні з часом?
Відповідь: Ця проблема подібна до попереднього Прикладу прикладу (5.6). Цей час, однак, ми хочемо знати середню концентрацію зерна. Маса Sr в часі t в сферичній оболонці товщини dr є:
M(t) = c(r, t)??r 2 dr
Середня концентрація Sr в зерні в часі t потім одержується за допомогою об'єднання і ділитися на об'єм:
C(t) 5.87
де c(r, t) заданий рівнянням 5.86 в Прикладі 5.6. Solutionis (Albarede, 1995):
C(t) = 5.88*
де Ci є початкова концентрація в calcite і C0 є концентрація в краї кришталя, який буде в рівновазі з водою пори.
Вирішення показане Фігура 5.15. Зерно досягає до рівноваги з водою пори всередині 100,000 до
200,000 років.
* Підсумовування в рівнянні 5.88 повільне, якщо Dt/ 2малий. Альтернативне вирішення рівняння
5.88 є:
C(t) = 5.89
Два вирішення дають однакові результати. Вони відрізняються тільки в легкості розрахунку. Для великих значень Dt/a2 підсумовуванню у 5.88 віддають перевагу. Для малих значень Dt/a2 5.89 віддають перевагу.
Фігура 5.15. Змініться в масовій концентрації Sr в 2 mm calcite діаметра зерновому набутті і початковій концентрації 2000 ppm, постійної концентрації у воді 10 пори ppm і коефіцієнті 100 calcite/вода розподілу.
Фігура 5.16. Електрон microprobe перетинає через прикордонні шари танучого в контакті з сферами кварцу поступово зникнення. Кварц є вліво в нульових мікронах. Зверніть увагу, що K2O і Na2O розповсюджують ‘uphill', тобто, в напрямку до вищих концентрацій K2O і Na2O в SiO2багатій рідині. Від Watson (1982).
5.4.3 Розповсюдження в Твердих тілах і Залежності Температури Коефіцієнта Розповсюдження
Ми можемо уявити собі чотири шляхи, в яких розповсюдження могло б мати місце в Фігурі твердих тіл (5.17):
1.) Обмін: обмін позиції двох атомів в сусідніх місцеперебуваннях.
2.) Interstitial: в якому атом пересувається від одного interstitial місцеперебування до іншого.
3.) Interstitialcy: в якому атом переставляється від місцеперебування структури в interstitial місцеперебування.
4.) Вакансія: в якому атом пересувається від місцеперебування структури до вакансії, створюючи вакансію ззаду цього.
Фігура 5.17. Чотири типи механізмів розповсюдження в твердих тілах. Після Broecker і Oversby (1971).
182
183
Механізми 1 і 3 включають зміщення двох атомів і таким чином мають високі енергії активації. Так як interstitial місцеперебування ймовірно малі, механізм 2 звернеться переважно до малих атомів (H і Він, наприклад ). Так, ми залишаємося з механізмом чотири, як головний механізм розповсюдження в твердих тілах.
Віднині, розповсюдження в твердих тілах є кусок подібно грі інформаторів: атом може взагалі тільки мандрувати за допомогою пересунення від місцеперебування структури до місцеперебування структури. До того ж, це може тільки пересунутися до вакантного місцеперебування структури (і один з відповідного типу). Взагалі, вакансії структури є двох типів: постійний і тимчасовий. Постійні вакансії можуть виникнути з дефектів або через наявність нечистот, наприклад через заміну вдвічі звинуваченого іона для окремо звинуватив будь-хто з вакансією, яка забезпечує баланс ціни. Тимчасові місцеперебування виникають з теплової агітації, яка примушує об'єм твердого тіла злегка бути більшою, ніж ідеальний об'єм за допомогою примушення атомів на поверхню. Номер колишнього є незалежна температура, недавні є залежна температура.
Давайте спробувати підрахувати коефіцієнт розповсюдження ab initio для простого одновимірного випадку розповсюдження дослідника в твердому відбувся через механізм вакансії. Так як конкретна мінімальна енергія вимагається, щоб вивести іон з енергії місцеперебування ‘структури well' ми повинні сподіватися, що ряд тимчасових вакансій має залежність форми температури рівняння 5.16, закону розподілу Boltzmann. Так, ряд вакансій структури може бути написаний, як:
Perm + Nvac=N k e А/RT
де k протягом деякого часу постійний і А є енергія активації, потрібна, щоб створити вакансію або ' діру'. Ймовірність, P, атомного створення успішний стрибок до вакантного місцеперебування знаходиться за допомогою збільшення ряд спроб, v, частками атомів, які мають достатню енергію, щоб не отримати добре:
P =? e EB /RT 5.94
Ряд спроб є просто розцінка вібрації,? ?, рази ряд дір:
?=??Чистити пилососом N =? ?Perm + N k e А /RT 5.95
Об'єднання 5.94 і 5.95, який ми маємо:
P =? ?Perm N EB /RT +? ?k e (EB +А )/RT
Розцінка розповсюдження повинна бути рядом разів стрибків відстань за стрибок, d:
P = 5.96
або perm P =mN e EB /RT +nk e (EB +А )/RT 5.97
де n і m є просто два constants, який замінює відповідні умови в рівнянні 5.96. Так, розцінки розповсюдження взагалі матимуть залежність температури, подібну до рівняння 5.24. У низькій температурі, постійні вакансії домінуватимуть і рівняння розцінки розповсюдження буде схожим:
perm mN e EB /RT 5.98
У вищій температурі, де теплово генеровані вакансії починають діяти, недавній строк в 5.97 домінує і рівняння розцінки розповсюдження буде схожим:
n e (EB +А )/RT 5.99
Розповсюдження, яке залежить від теплово створених вакансій, інколи зветься притаманне розповсюдження, що залежність на постійних вакансіях зветься стороннє розповсюдження. Кордон між цими регіонами поміняється, залежно від природи матеріалу і теперішнього часу
183
184
нечистот. Для NaCl, перехід відбувається навколо 500°C, для силікатів це взагалі відбувається над 1000° C. Де механізм розповсюдження змінюється, розрив в нахилі може спостерігатися на кресленні vs lnD. 1/T. Наприклад, Фігура 5.18 показує те, як коефіцієнт розповсюдження міг би змінитися основаним на рівняннях 5.98 і 5.99.
Об'єднуючи EB і А в єдиний строк енергії активації, EA, який є енергія, необхідна, щоб створити вакансію і пересунути інший атом в це, типовий вираз для залежності температури коефіцієнта розповсюдження в твердих тілах є:
D=D o e EA /RT 5.100
де Робота знову зветься частотний фактор. Оскільки ми дивилися, це залежатиме від vibrational частоти і відстані внутрішньоатомного стрибка.
Експериментальне спостереження підтримує наше теоретичне чекання експонентної залежності розповсюдження температури, наприклад, в серії вимірювань коефіцієнта розповсюдження, D, в різній Фігурі температур (5.19). Беручи колоду обох сторін рівняння 5.98, ми одержуємо:
ln D=EART +lnD o
Так на кресленні lnD проти взаємної температури, дані для розповсюдження даного елемента по даній суті повинні креслити план один лінію з нахилом EA/R і стати на перешкоді Фігуру D o (5.19). Значення для енергії активації взагалі подібні для найбільших елементів (звичайно 50 до 200 kJ), але частотний фактор міняється широко. Табличні 5.2 спискові частотні фактори і енергії активації для декількох елементів в різних геологічних матеріалах.
Фігура 5.19. Схематичне креслення розцінки розповсюдження колоди проти протилежності температури (Креслення Arrhenius ) для двох елементів: Cs і Sr.
МАЛ. 5.18. Креслення Arrhenius illustrating те, як зміна в механізмі розповсюдження від притаманного до стороннього може закінчитися розривом в нахилі.
Залежність тиску коефіцієнта розповсюдження є:
D=D o e (EA +(P 1)?)(V) / RT 5.101
де V є “об'єм активації ".
5.4.4 Розповсюдження в Рідинах
Як В рідинах так і твердих тілах, коефіцієнти розповсюдження залежать як від природи родів розповсюдження так і природи прес. Оскільки ви могли б очікувати, малі атоми взагалі розповсюджують більш стрімко, ніж великі іони. Значення коефіцієнта розповсюдження в рідинах може бути оцінене в ряді шляхів. Оснований на моделі молекулярного руху і набуття кінетичної енергії за атом 3kT/2, коефіцієнт розповсюдження може бути оцінений, як (Krikaldy і Молодий, 1985):
D? ??d 8k? ?m T 3/2 5.102
де "a"? є коефіцієнт теплового розширення, "d" є молекулярний діаметр, "m" є молекулярна маса і k, як звичайно, є Boltzmann's постійний. Це передбачає коефіцієнт розповсюдження біля плавкої точки 10-4 cm/сухий.
Коефіцієнти Розповсюдження в рідинах також просто виражаються в строк в'язкості. Для uncharged родів, залежність коефіцієнта розповсюдження на іонному радіусі і в'язкості виражається Einstein, що Підтримує вогонь, Рівнянням:
D = kT?r 5.103
184
185
де "r" є іонний радіус,'ню"? ?є в'язкість, і, як звичайно, k є Boltzmann's постійний і T є температура. Від цього рівняння, ми бачимо, що розповсюдження стає більш важким, як рідина стає більш структурним (полімеризований), через те, що в'язкість зростає з полімеризацією зрощення.
Через електричний ефект нейтралітету, ціна іона є важлива в розповсюдженні іонів. У водних електролітах, коефіцієнти розповсюдження дослідника залежать від ціни іона, як:
= 5.104
де "°" є іонна електропровідність обмеження (електропровідність extrapolated до безмежного розбавлення). F є Faraday's постійний, і z є ціна іона. Нуль (°) означає стандартний стан безмежного розбавлення. У більш зосереджених вирішеннях, коефіцієнти розповсюдження показують комплексну залежність від іонної сили, ставлення яких є по той бік меж цієї книги. Обговорення цієї проблеми можуть бути знайдені в Anderson (1981) і Tyrell і Harris (1984).
185
186
Таблиця 5.2а Енергія активації (EA) і частотний фактор (D0) при дифузії мікродомішок в мінералах
Елем |
Фаза |
Температурний |
D0, см2/с |
EA kJ/mol |
ент |
|
діапазон, °C |
|
|
Fe |
олівін |
1125-1200 |
5.598*10-02 |
264 |
Fe |
олівін |
1000-1125 |
5.90*10-07 |
133 |
Mg |
олівін |
1000-1150 |
1.82*10-08 |
143 |
Mn |
гранат |
750-1475 |
5.15*10-04 |
145 |
Fe |
гранат |
750-1475 |
6.39*10-04 |
157 |
O |
-кварц |
1010-1220 |
3.70*10-13 |
230 |
O |
анортит |
800-1300 |
9.00*10-10 |
234 |
Cr |
шпінель |
1200-1600 |
2.40*10-06 |
337 |
Pb |
плагіоклаз |
700-1050 |
1.86*10-03 |
266 |
Pb |
K-польовий шпат |
700-1050 |
1.82*10-01 |
309 |
Sr |
плагіоклаз |
700-1050 |
1.78*10-03 |
265 |
Sr |
ортоклаз |
800-870 |
6.00*10-06 |
98 |
Na |
альбіт |
600-800 |
0.125 |
100 |
H2O |
обсидіан |
500-980 |
1.50*10-08 |
27 |
Таблиця 5.2б Енергія активації (EA), частотний фактор (D0) і коефіцієнти дифузії (D) при дифузії мікродомішок катіонів в двох типах магматичних розплавів
|
|
Розплав |
D, см2/с |
D0, см2/с |
EA kJ/mol |
Sr |
1250-1450 |
базальтовий |
|
0.278 |
104 |
Sr |
1300-1400 |
андезитовий |
|
3.5 |
213 |
Ca |
1250-1450 |
базальтовий |
|
0.535 |
105 |
Ba |
1250-1450 |
базальтовий |
|
0.059 |
94 |
Ba |
1300-1400 |
андезитовий |
|
0.44 |
209 |
Cs |
1300-1400 |
базальтовий |
|
110 |
272 |
Co |
1250-1450 |
базальтовий |
|
0.053 |
86 |
Co |
1300-1400 |
андезитовий |
|
160 |
280 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.5 Поверхні, Інтерфейси, і Процеси установлення інтерфейсу
Якості фази в поверхні відмінні від масових якостей фази. Ця різниця виникає з різниці між місцевим оточенням атомів на поверхні або інтерфейсі і тих у внутрішній частині фази. Атом в поверхні кришталя не оточується тими ж зобов'язаннями і розподілом витрат, оскільки це повинне бути у внутрішній частині кришталевої структури. Потенційна енергія повинна таким чином відрізнитися. Тут ми визначаємо поверхню, як зовнішній кордон згущеної фази (тверде тіло або рідина) у вакуумі або газі. Інтерфейс є кордон між двома згущеними фазами, наприклад, між 2 кришталя або між мінералом і водою (строк ‘surface' є, однак, часто використаний для того, що ми тільки визначили, як інтерфейс). Поверхні, зовнішні енергії, і інтерфейси грають важливу роль в багато geochemical процесах. Всі різнорідні реакції, тобто, ті, включаючи більш ніж 1 фазу, повинні завжди включити інтерфейси або поверхні. Розчинення, плавлення, ex вирішення, і
186
187
навальність є приклади процесів, що, на атомній шкалі, відбуваються цілком в або біля інтерфейсу між двома фазами. Поверхні можуть також грати важливі ролі, як каталізатори в багато geochemical реакціях.
На мікроскопічній шкалі, реактивність мінеральних поверхонь поміняється у певному місці з декількох причин. Початок є microtopography зовнішньої (Фігури 5.20). Наприклад, єдина одиниця (який міг би бути єдиним атомом, іоном, або молекулою і викликав adatom)зростання, розміщена на інакшій плоскій поверхні особливо буде нестійка, через те, що це зв'язується до інших одиниць на тільки одній стороні. Крок (який міг би бути сформований через зростання, розчинення, або гвинтовий розлад) забезпечує більш сприятливе місцеперебування зростання, через те, що нова одиниця прив'язана до інших одиниць на 2 сторін. Навіть краще місцеперебування для зростання є в перекрученні, де зобов'язання можуть бути сформовані на 3 сторін. Протилежно, одиниця в перекрученні (з 3 виставленими сторін) менше стійка, і віднині більш вразливий до розчинення, ніж будь-хто в кроці (з 2 виставленими сторін), який по черзі менше стійкий, ніж одиниця на плоскій поверхні, тільки з 1 виставленою стороною. Точка є, перекручення і кроки більш будуть реагуючі, ніж інший зображає, так що зовнішні розцінки реакцій залежатимуть в частині на щільності цих ознак.
Якості мінеральних поверхонь також поміняються залежно від орієнтації поверхні відносно crystallographic сокир. Найбільші мінерали ростуть або наплив, швидший в одному напрямку, ніж в іншому. Найбільші зовнішні реакції включають утворення нових зобов'язань між атомами мінерала і атомами сусідньої фази; природа зобов'язань, які є можливі залежатиме від орієнтації поверхні відносно crystallographic сокир. Розцінки Реакції, які вимірюються для одного кришталевого лиця, не можуть бути характерні з інших лиць.
Накінець, майже всі мінерали мають різноманітність атомів і crystallographic місцеперебувань, віднині буде різноманітність зобов'язань, які можливі на будь-якій поверхні. Ми обговоримо цей аспект поверхонь детально злегка більший нижче.
Крок; Розташувати терасами; Addatom; Перекручення; Гвинтовий Розлад; Яма
Фігура 5.20. На мікроскопічній шкалі, поверхня мінерала показує ряд ознак. У результаті, місцева реактивність поверхні цілком буде мінлива.
5.5.1 Зовнішня Вільна Енергія
У Розділах 2 і 3, ми представили поняття кутніх кількостей і часткових кутніх кількостей. Наприклад, кутній об'єм субстанції був:
V = V/n
і ми визначили частковий кутній об'єм, як:
v я? ?=? V?n я T, P, n j (3.11)
Ми в даний момент визначаємо 2 нових кількостей, кутню зовнішню область:
=5.105
і часткова кутня зовнішня область:
я? ?=?? n я T, P, n j 5.106
де є зовнішня область фази. Кутній об'єм або кутня Вільна Енергія Gibbs чистого кварцу залежить тільки від температури і тиску. Так, кутній об'єм або кожний (чистий) кварцовий кришталь той же, що і те кожного іншого (чистий) кварцового кришталя в тій температурі і тиску. На відміну від інших кутніх кількостей, кутня зовнішня область і часткова кутня зовнішня область залежать від форми і розміру, і є таким чином не притаманні якості субстанції. Для сфери, наприклад, часткова кутня зовнішня область зв'язана з кутнім об'ємом, як:
187
188
=? =2V r 5.107
Для інших форм, стосунки між s і v відрізняться.
Накінець, ми визначаємо зовнішню вільну енергію фази Ф, як:
??????G?AT, P, n5.108
Зовнішня вільна енергія представляє ті енергетичні ефекти, які з'являються, через різницю в атомному оточенні на поверхні фази. Зовнішня вільна енергія ретельно зв'язана із зовнішньою напруженістю. Повна зовнішня вільна енергія фази мінімізується за допомогою мінімізації зовнішньої області фази. Так, водна капля у відсутності інших сил піклуватиметься, щоб сформувати сферу, форму, яка мінімізує зовнішню область. Коли зовнішні ефекти повинні бути розглянуті, ми можемо виправити рівняння (Вільної Енергії Gibbs equ. 3.14) щоб бути:
dG = VdP SdT +? я dn я? ?я +? ?k dA k? ?k 5.109
де остання сума приймається над всіма інтерфейсами системи. У цьому почутті різні crystallographic лиця мають різні зовнішні вільні енергії. Останній строк в 5.109 зростає у важливості, як розмір зменшується. Це є, через те, що зовнішня область для даного об'єму або маси фази буде найбільша, коли розмір частки малий.
5.5.2 Ефект Кіловат-години
Коли розмір фаз, які включаються достатньо малий, зовнішня вільна енергія може мати ефект рівноваги переставлення. Для системи рівноваги в постійній температурі і тиску, рівняння 5.109 стає:
0 =
Перший строк на праві є G°, який відповідно до 3.86 рівний до RTlnK. Це є ‘постійна рівновага normal', неупереджене зовнішньою вільною енергією, так що ми повинні викликати це K°. Підсумовування в другому строку є також постійна рівновага, який ми викличемо K s, рівновагу, яка впливається зовнішньою вільною енергією. Роблячи ці заміни і повторне впорядкування, ми маємо:
ln K s =ln? k dAk?RT 5.110
Так, ми передбачаємо, що рівновага може бути переміщена завдяки зовнішній вільній енергії, і переміщення залежатиме від зовнішньої або interfacial області. Це відоме, як Ефект Кіловатгодини. Є ряд прикладів цього ефекту. Наприклад, штраф, і таким чином висока зовнішня область, частки більш розчинні, ніж грубіші частки того ж складу. Вода має зовнішню вільну енергію близько 70 mJ/m2. Отже, вогкість в хмарах і імлі може досягнути до 110%, коли розмір капельки малий.
188
189
10. 3 Зародкоутворення і ріст кристалів в розплаві
10.3.1 Утворення зародків кристалів
При охолодженні рідкої магми за певної температури виникає ситуація коли магма виявляється насиченою по відношенню до розчинених мінеральних фаз. Рідини (як силікатні розплави, так і розчини: морська вода, наприклад, на поверхні є перенасиченою по відношенню до кальциту) взагалі часто є суттєво перенасиченими по відношенню до деяких мінеральних фаз ще до початку кристалізації. Однак кристалізація мінеральних фаз з перенасичених розчинів (розплавів) відбувається лише після додавання (та/або утворення) певної кількості початкових зародків, коли стане можливим утворення і ріст дрібних кристалів.
Оскільки кристали зароджуються і ростуть при температурі більш низькій ніж та за якої вони могли б розплавитись в магмі (розчинитись в розчині?) то така магма називається переохолодженою. До початку кристалізації вона знаходиться в метастабільному стані. Існування такого метастабільного стану обумовлене тим що за низького рівня перенасичення рідини будьякий новоутворений зародок кристалу швидко руйнується молекулярним рухом (раніше ніж зародок встигає вирости до стійкого розміру. Перенасичення є рушійною силою росту кристалів, і, певною мірою, чим більшою є ступінь перенасичення, тим швидше кристали ростуть. Тому існує певний рівень перенасичення, за якого вірогідність зростання кристалічного зародку стає вищою ніж руйнування. Параметри метастабільної області (діапазон температур, тисків, концентрацій тощо) залежать від великої кількості чинників, таких як швидкість охолодження магми, швидкість руху магми тощо. Магма може стати насиченою відносно певних мінеральних фаз не тільки при простому охолодженні, але й при інших процесах чи при комбінації останніх з остиганням. Наприклад, на ранніх стадіях фракціонування основної магми не відбувається кристалізація фосфатних мінералів і з ростом ступеню фракціонування в залишковому розплаві кількість фосфору безперервно зростає аж до тих пір поки концентрація і температура не стануть достатніми для зародження і росту кристалів апатиту.
В складних силікатних розплавах і магмах мінерали, які кристалізуються, за складом відрізняються від складу магми. Кристалізація може продовжуватись доти, допоки магма буде пересиченою відносно твердої фази на певну величину. Швидкість утворення зародків, швидкість росту кристалів і порядок в якому різні мінерали починають кристалізуватись з остигаючої магми є важливими чинниками, що контролюють формування різноманітних структур магматичних порід.
Зародження кристалів можливе у випадку якщо при їх утворенні знизиться вільна енергія (G) системи. Однак на початковому етапі утворення зародків кристалів супроводжується зростанням вільної енергії порівняно з рівноважною величиною. Це зростання обумовлене вкладом поверхневої вільної енергії новоутворюваних кристалів. Тому кристалізація буде йти лише в тому випадку якщо зниження вільної енергії всієї системи буде більшим ніж надлишкова вільна енергія, яка виникає при утворенні поверхні розділу розплав - тверде тіло, і зростає надалі при збільшенні площі кристалів.
Такі умови існують лише у випадку коли розплав чи магма пересичені по відношенню до одної чи кількох мінеральних фаз. Повна зміна вільної енергії для кристалу який зростає в рідині дорівнює:
dGtot= dA+dGr |
5.111 |
де - питома поверхнева енергія, а dGr позначає власне зміну вільної енергії кристалізації в зв’язку з утворенням об’єму кристалу (тобто вільна енергія фазового переходу в звичному розумінні, без поверхневих ефектів).
189
190
Розглянемо більш конкретну задачу - зміну вільної енергії при формуванні сферичного кристалу фази , який виростає з розчину (розплаву) того ж складу. В цьому випадку зміна вільної енергії G системи може бути виражена рівнянням:
|
2 |
|
3 |
Gr/V) |
5.112 |
dGtot=4 r |
+(4/3) |
r |
( |
|
де r є радіусом кристалу (ми ділимо G на V, для того щоб перейти від джоулів/моль до джоулів/одиницю об'єму). Перша компонента є вільною поверхневою енергією, вона завжди позитивна. В точці де розчин точно стає насиченим Gr буде рівним 0. Чиста вільна енергія, Gtot, в цьому випадку є позитивною, і кристал буде розчинятися. Для того, щоб спонтанне утворення зародків відбувалося другий член рівняння 5.112 має бути негативним і за величиною перевищувати перший член. Тобто, для початку процесу утворення зародків рідина повинна бути перенасиченою. Вирішуючи 5.112 для r, ми знаходимо, що Gtot 0 тоді, коли r -3( / Gr).
Як змінюватиметься G починаючи r до цієї точки? Щоб відповісти на це цьому, ми розв’язуємо
5.112 щодо r:
( |
|
Gtot/ |
|
r)=8 |
|
|
|
2 |
Gr/V) |
5.113 |
|
|
r |
+4 |
r |
( |
|
Так як вираз що описує зміну вільної енергії об'єму містить r2, то зміна поверхневої енергії обов'язково домінуватиме в області дуже малих значень r. Для малих значень r, Gtot зростатиме із зростанням r кристалу тому що завжди позитивна. Іншими словами, біля точки насичення, деGrl є малим, дуже малі зерна ставатимуть все нестабільнішими в міру свого зростання.
Критичне значення r, значення після якого G буде зменшуватись при подальшому зростанні радіусу, знаходиться в точці Gtot/ r=0. Розв'язуючи рівняння 5.113, ми знаходимо
rcrit=-2 /( Gr/V) |
5.114 |
|
|
|
(Тут ми можемо побачити, що для збереження розмірностей, |
нам слід підставляти значення |
|||
|
вільної енергії нормованими на одиницю об’єму |
|||
|
а не на моль). |
|
|
|
|
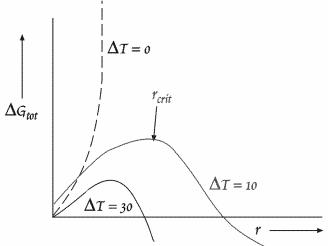
Рисунок 5.21. Вільна енергія, як функція радіусу |
|||
|
зародку для малих кристалів які формуються |
|||
|
поблизу точки насичення. T є мірою |
|||
|
переохолодження (різниця між температурою |
|||
|
розчину/розплаву і температурою насичення ). |
|||
|
Для розчину (розплаву), який охолоджується і |
|||
|
стає все більш насиченим (наприклад, магма або |
|||
|
охолоджуючийся гідротермальний розчин), для |
|||
|
знаходження складової Gr |
ми можемо |
||
|
використовувати |
|
рівняння 5.68 |
(тобто Gr=- |
|
T S, де T є різницею між реальною |
|||
|
температурою |
і |
температурою |
при якій |
відбувається насичення, S є зміною ентропії при кристалізації). На рис.5.21 показана сумарна вільна енергія, підрахована описаним шляхом, як функція r для різних стадій переохолодження.
Поверхнева складова вільної енергії корелює з в'язкістю. Тому зародкоутворення у водних розчинах має відбуватися за менших величин перенасичення ніж у силікатних розплавах. Для силікатних розплавів слід вважати більшою швидкість кристалізації в основних розплавах, які мають відносно низьку в’язкість, порівняно з кислими розплавами, в'язкість яких вища. Цей доконаним фактом. Також, ми можемо передбачати більше перенасичення при стрімкому охолодженні (порівняно з повільним охолодженням). Це пов’язано з тим що існує певна
190
