2. Поверхности нелинейчатые

Различают нелинейчатые поверхности с образующей переменного вида и с образующей постоянного вида.

Поверхности с образующей переменного вида имеют определитель

(a, m)[A,A₁],

где a— образующая переменного вида;

m — направляющая;

A— закон перемещения образующей по направляющей;

A₁- закон изменения формы образующей.

Примером нелинейчатой поверхности с образующей переменного вида может служить каналовая поверхность (рис. 127).

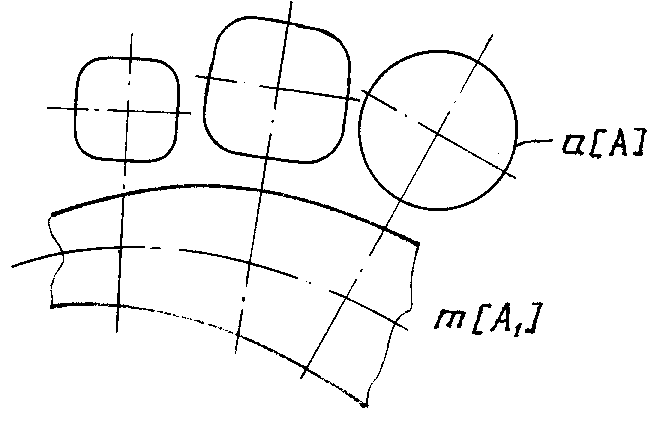
Рис. 120

Каналовая поверхность — поверхность, образованная каркасом замкнутых плоских сечений, определенным образом ориентированных в пространстве. Площади этих сечений монотонно изменяются в процессе их перемещения по направляющей.

Плоскости образующих ориентируют в инженерной практике двумя способами:

— параллельно какой-либо плоскости (каналовые поверхности с плоскостью параллелизма);

— перпендикулярно к направляющей линии (нормальные или прямые каналовые поверхности). Нормальная каналовая поверхность показана на рис.

Циклическая поверхность — частный случай каналовой (рис. 128).

Рис. 121

Она образуется окружностью, центр которой перемещается по криволинейной направляющей.

Поверхность с образующей постоянного вида имеет определитель

(a, m)[A],

где a— образующая;

m — направляющая;

A— закон перемещения образующей.

Примером является трубчатая поверхность, которая получается при движении центра окружности постоянного диаметра (образующая) по криволинейной направляющей; плоскость окружности все время остается перпендикулярной к направляющей (рис. 129).

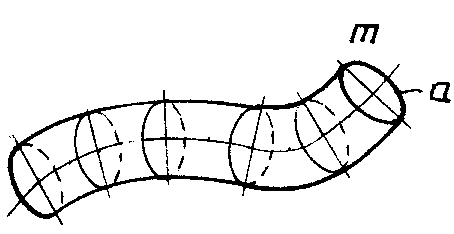
Рис. 122

По форме образующей — частный случай циклической поверхности.

По закону движения образующей — частный случай каналовой поверхности.

Трубчатая поверхность может быть получена движением сферы постоянного диаметра.

3. Поверхности параллельного переноса, вращения и винтовые

Классификация поверхностей по форме образующей (линейчатые и нелинейчатые) учитывает геометрическую часть определителя. По характеру алгоритмической части определителя, т.е. по закону движения образующей (как прямой, так и кривой линии) можно выделить поверхности:

— параллельного переноса, которые образуются поступательным перемещением образующей линии;

— вращения, образованные вращательным перемещением образующей линии;

— винтовые, образованные винтовым перемещением образующей.

Эти поверхности имеют широкое применение в машиностроении как наиболее экономичные в связи с удобством формообразования на станках, например, строганием или фрезерованием (некоторые поверхности параллельного переноса), точением на токарном (поверхности вращения) или токарно-винторезном (винтовые поверхности) станке.

Иногда эти поверхности называют кинематическими поверхностями, поскольку в основу их классификации положен характер движения образующей.

ПОВЕРХНОСТИ ПАРАЛЛЕЛЬНОГО ПЕРЕНОСА

Поверхностью параллельного переноса называется поверхность, образованная параллельным переносом образующей линии.

Параллельный перенос — такое перемещение фигуры, при котором все точки перемещаются в одном и том же направлении на одно и то же расстояние.

Простейшим примером поверхности параллельного переноса может служить цилиндрическая (призматическая) поверхность, если рассматривать ее как образованную поступательным перемещением направляющей кривой (ломаной) линии (рис. 116 и рис. 117) по образующей, т.е. по направлению s . Причем здесь направляющая цилиндрической (призматической) поверхности становится образующей поверхности параллельного переноса, а образующая — направляющей этой поверхности.

В общем случае у поверхности параллельного переноса, имеющей определитель

(a, m)[A],

где a— образующая;

m — направляющая;

[A]— условие параллельного перемещения точек образующей,

направляющая может быть кривая, в отличие от цилиндрической (призматической) поверхности переноса, где направляющая, очевидно — прямая.