1.3. Метод Крамера

Отыскание решения системы по теореме Крамера называют методом Крамера решения системы линейных уравнений.

Теорема Крамера. Пусть  – определитель матрицы системы А; _j – определитель матрицы, получаемой из матрицы А заменой j- го столбца столбцом свободных членов. Тогда, если   0, то система имеет единственное решение, определяемое по формулам:

, j = 1, 2, …, n

Эти формулы называются формулами Крамера.

Пример 2. Решить систему линейных уравнений методом Крамера.

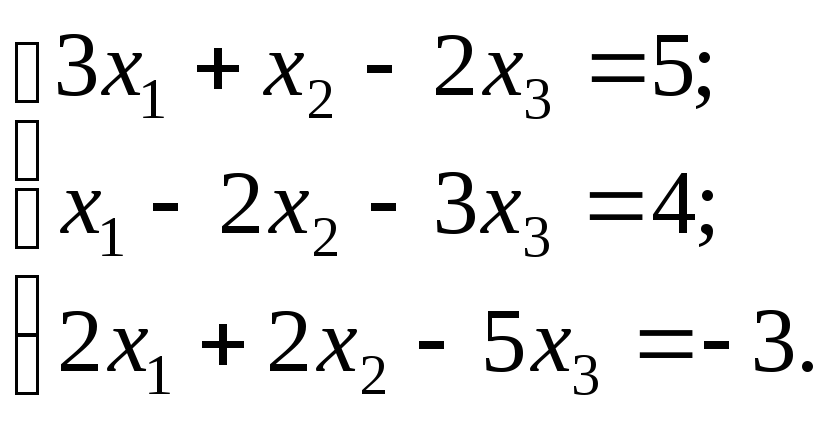
Решение.

Найдем общий определитель системы:

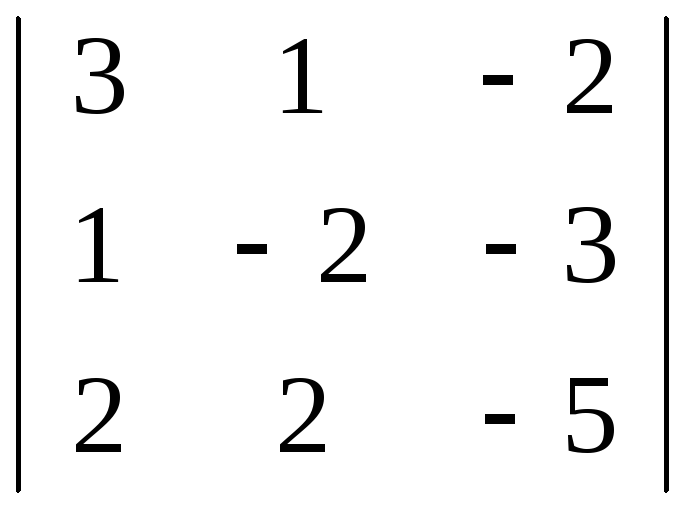∆ = = 3∙(–2) ∙(–5) + 1∙(–3) ∙2 + 1∙2∙(–2) – (–2) ∙(–2) ∙2 –

– 2∙(–3) ∙3 – 1∙1∙(–5) = 30 – 4 – 6 – 8 + 18 + 5 = 35.

Вычислим определители переменных ∆₁, ∆₂, ∆₃, которые получаются из общего определителя заменой соответствующего столбца столбцом свободных членов (правых частей каждого уравнения):

∆₁ = = 5∙(–2) ∙(–5) + 1∙(–3) ∙(–3) + 4∙2∙(–2) – (–2) ∙(–2) ∙(–3) –

– 2∙(–3) ∙5 – 1∙4∙(–5) = 50 + 9 – 16 + 12 + 30 + 20 = 105.

∆₂ = = 3∙4∙(–5) + 1∙(–3)∙(–2) + 5∙(–3)∙2 – (–2)∙4∙2 – (–3)∙(–3)∙3 –

– 1∙5∙(–5) = – 60 + 6 – 30 + 16 – 27 + 25 = – 70.

∆₃ = = 3∙(–2) ∙(–3) + 1∙2∙5 + 1∙4∙2– 5∙(–2)∙2 – 2∙4∙3 – 1∙1∙(–3) = = 18 + 10 + 8 + 20 – 24 + 3 = 35.

Решение системы линейных уравнений найдем по формулам Крамера:

x₁ = ; x₂ = ; x₃ = .

1.4. Метод Гаусса

Универсальным методом решения системы линейных уравнений является метод Гаусса – метод последовательного исключения переменных.

Он заключается в том, что с помощью элементарных преобразований система уравнений приводится к эквивалентной системе ступенчатого или треугольного вида (прямой ход Гаусса). Из этой системы последовательно, начиная с последних (по номеру) переменных, определяются остальные переменные (обратный ход Гаусса).

Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицей их коэффициентов. Система линейных уравнений записывается в виде расширенной матрицы системы, в которой кроме матрицы системы А, дополнительно включен столбец свободных членов В:

.

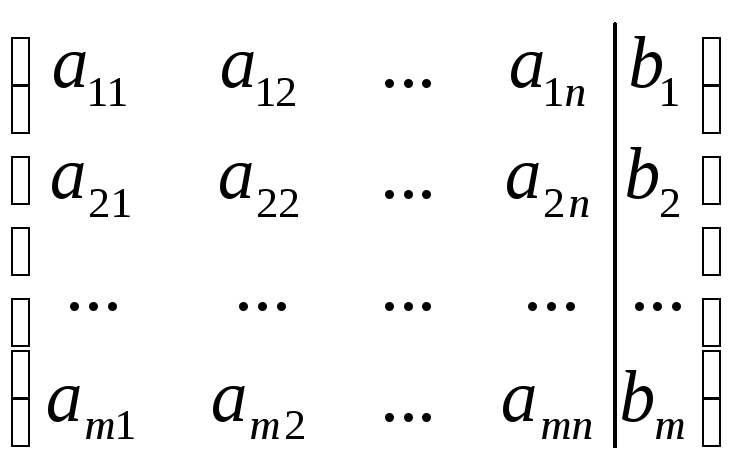Разновидностью метода Гаусса является метод полного исключения переменных. Расширенная матрица с помощью элементарных преобразований приводится к матрице вида:

.

По последней расширенной матрице восстанавливается система линейных уравнений и находится ее решение.

Пример 3. Решить систему линейных уравнений методом Гаусса:

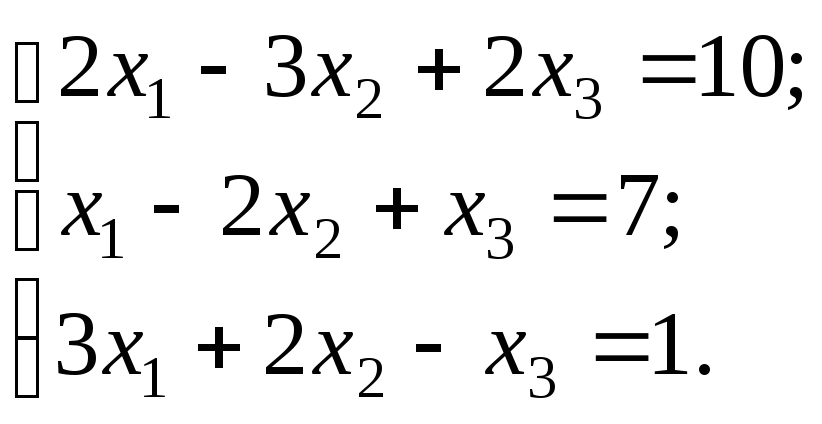
Решение.

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем к единичной матрице в основной части.

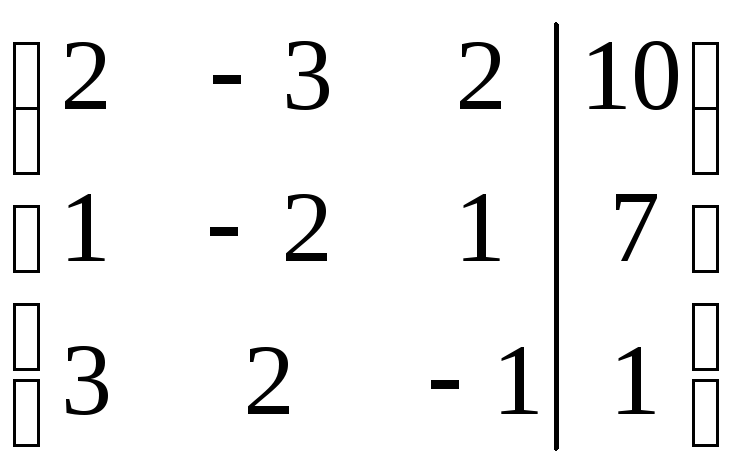
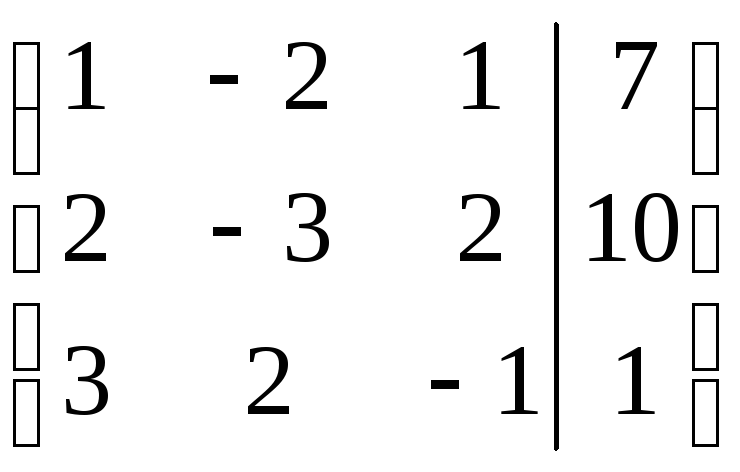
× 2

× (-3)

:(-4)

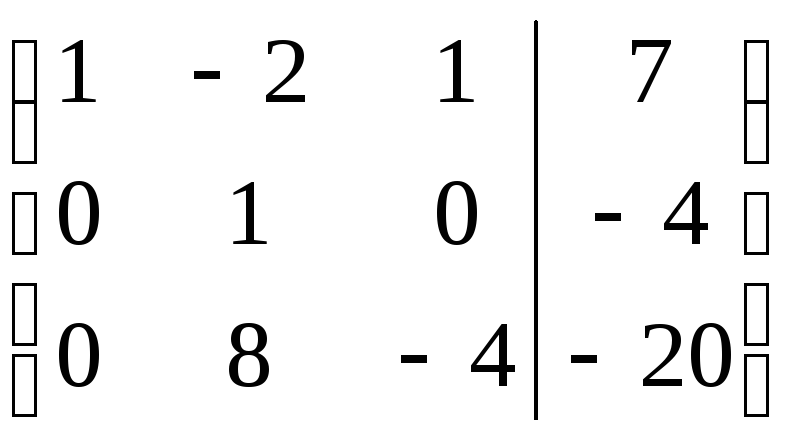
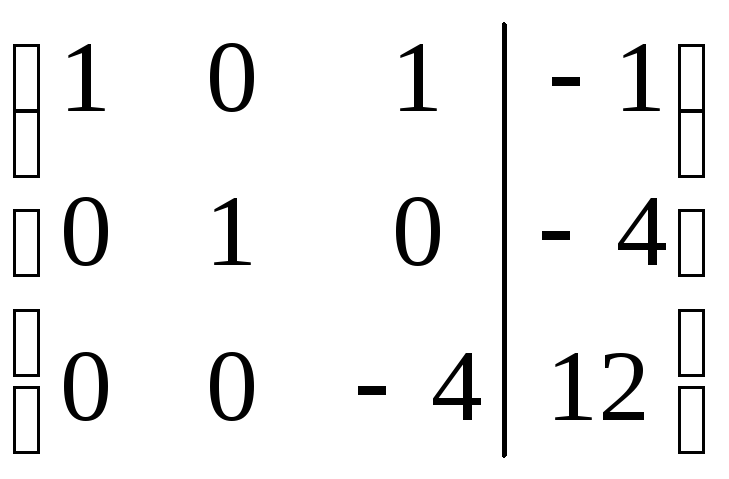
× (-1)

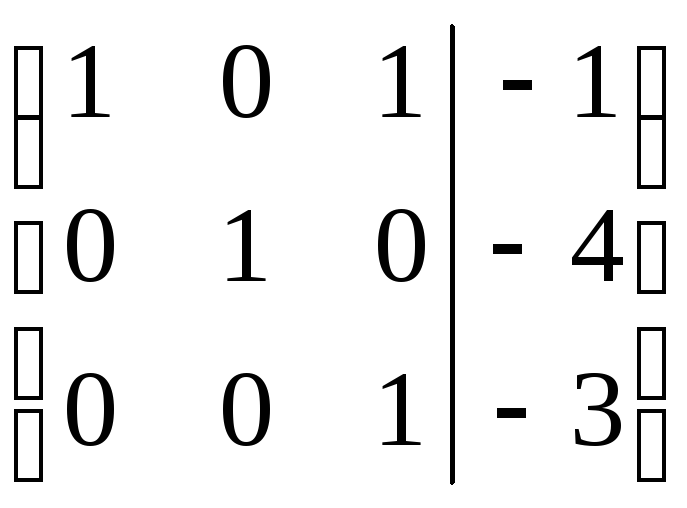
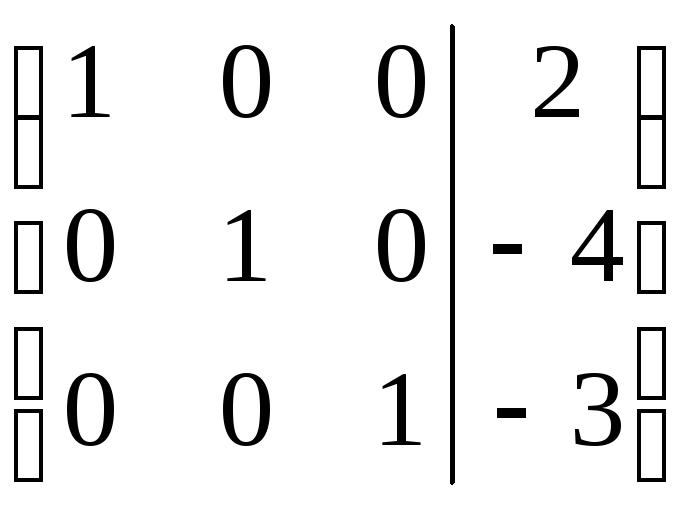
Восстанавливая последнюю расширенную матрицу системы, получим решение системы линейных уравнений:

Ответ: х₁ = 2, х₂ = –4, х₃ = –3.

1.5. Вопросы для самоконтроля

1. Что называется матрицей?

2. Какие бывают виды матриц?

3. Каковы основные действия над матрицами?

4. Какая матрица называется невырожденной?

5. Какая матрица называется обратной по отношению к данной матрице?

6. Сформулируйте правило нахождения обратной матрицы.

7. Что называется рангом матрицы?

8. Как найти ранг матрицы?

9. Что называется определителем второго, третьего, п-го порядков?

10. Перечислите основные свойства определителей.

11. Что называется минором, алгебраическим дополнением элемента определителя?

12. В чем заключается теорема Лапласа?

13. Дайте определение системы линейных алгебраических уравнений.

14. Сформулируйте теорему Кронекера-Капелли.

15. Напишите формулы Крамера решения системы линейных уравнений. В каких случаях их можно использовать?

16. Опишите матричный способ решения системы линейных уравнений.

17. Опишите схему решения системы линейных уравнений методом Гаусса.

18. Как найти решение системы линейных однородных уравнений?

19. Какова геометрическая интерпретация системы линейных уравнений и неравенств?