
- •Министерство аграрной политики украины
- •Издание рассмотрено и рекомендовано к печати на заседании кафедры физико-математических дисциплин (протокол № 2 от 9 октября 2007г.);
- •Содержание
- •1. Линейная алгебра
- •1.1. Системы линейных уравнений
- •1.2. Метод обратной матрицы
- •1.3. Метод Крамера
- •1.4. Метод Гаусса
- •1.5. Вопросы для самоконтроля
- •2. Аналитическая геометрия на плоскости
- •2.1. Линии первого порядка
- •2.2. Линии второго порядка Окружность
- •Гипербола
- •Парабола
- •2.3. Вопросы для самоконтроля
- •3. Векторная алгебра
- •3.1. Основные определения и понятия
- •3.2. Скалярное произведение векторов
- •3.3. Векторное произведение векторов
- •3.4. Смешанное произведение векторов
- •3.5. Вопросы для самоконтроля
- •4. Аналитическая геометрия в пространстве
- •4.1. Плоскость в пространстве
- •4.2. Прямая в пространстве
- •4.3. Прямая и плоскость в пространстве
- •4.4. Вопросы для самоконтроля
- •Литература
- •Индивидуальные задания к расчётно-графической работе Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Для выполнения ргр
- •211 Группа
- •212 Группа
- •213 Группа
- •214 Группа
- •215 Группа
- •311 Группа
- •312 Группа
- •313 Группа
- •314 Группа
- •315 Группа
- •316 Группа
- •1111 Группа
- •1112 Группа
- •1211 Группа
- •1212 Группа
- •1311 Группа
- •1312 Группа
- •1313 Группа
- •1511 Группа
- •1512 Группа
3.3. Векторное произведение векторов
Векторным
произведением
двух векторов
![]() и
и![]() называется вектор
называется вектор![]() ,
обозначаемый
,
обозначаемый![]() ,
который удовлетворяет следующим
условиям:
,
который удовлетворяет следующим
условиям:
вектор
 перпендикулярен плоскости, в которой
лежат векторы
перпендикулярен плоскости, в которой
лежат векторы и
и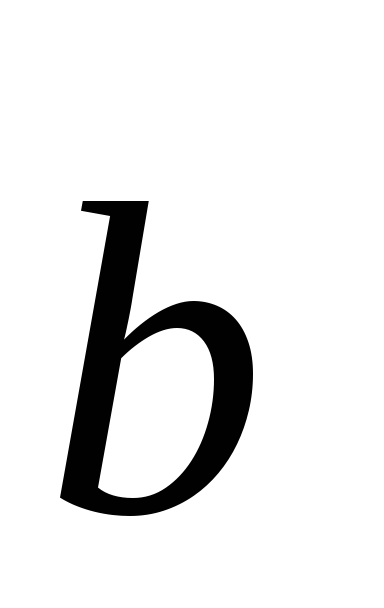 ;
;вектор
 имеет длину, численно равную площади
параллелограмма, построенного на
векторах
имеет длину, численно равную площади
параллелограмма, построенного на
векторах и
и как на сторонах:
как на сторонах:
![]() ,
где α – угол между векторами
,
где α – угол между векторами
![]() и
и![]() ;
;
векторы
 ,
,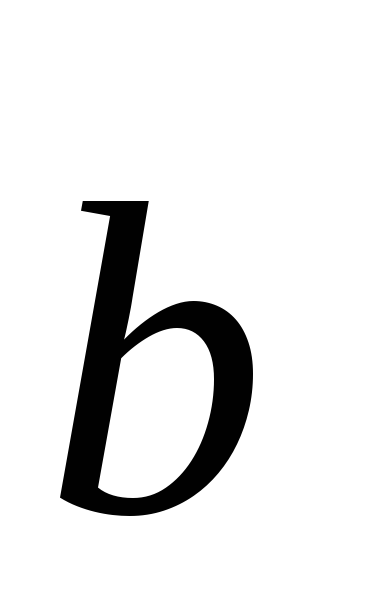 ,
, образуют правую тройку.
образуют правую тройку.

Рис. 17
Т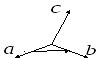 ри
произвольных некомпланарных вектора
ри
произвольных некомпланарных вектора![]() ,
,![]() ,
,![]() ,
взятые в указанном порядке, образуютправую тройку,
если с конца третьего вектора
,
взятые в указанном порядке, образуютправую тройку,
если с конца третьего вектора
![]() кратчайший поворот от первого вектора
кратчайший поворот от первого вектора![]() ко второму вектору
ко второму вектору![]() виден совершающимся против часовой
стрелки (рис. 18), илевую,
если по часовой стрелке.
виден совершающимся против часовой
стрелки (рис. 18), илевую,
если по часовой стрелке.
Рис. 18
Если
система координатных осей правая и
векторы
![]() и
и![]() заданы своими координатами,
заданы своими координатами,![]() ,
,![]() ,
товекторное
произведение
,
товекторное
произведение
![]() определяется по формуле:
определяется по формуле:
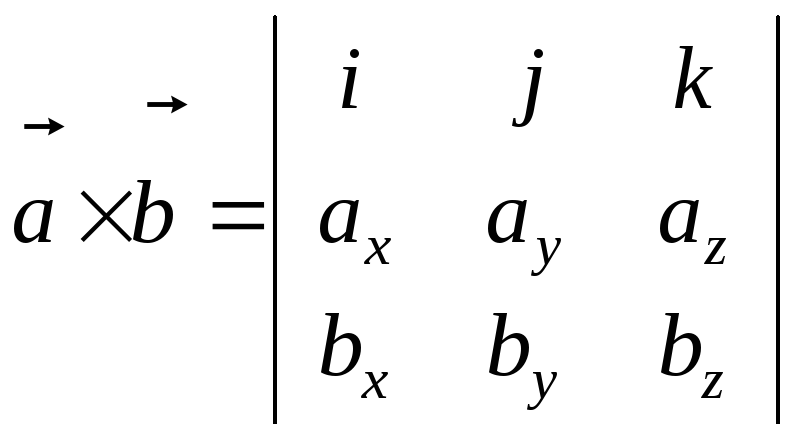 .
.
Площадь
параллелограмма S,
построенного на векторах
![]() и
и![]() ,
равна модулю векторного произведения
,
равна модулю векторного произведения![]() ×
×![]() и определяется по формуле:
и определяется по формуле:
S
= |![]() |.
|.
Площадь
треугольника S,
построенного на векторах
![]() и
и![]() ,
равна половине площади параллелограмма:
,
равна половине площади параллелограмма:
SΔ
=
![]() S
=
S
=
![]() |
|![]() |.
|.
3.4. Смешанное произведение векторов
Смешанным
произведением
трех
векторов
![]() ,
,![]() ,
,![]() называется число, равное векторному
произведению
называется число, равное векторному
произведению![]() ,
умноженному скалярно на
,
умноженному скалярно на![]() :
:![]() .
.
Смешанное
произведение равно объему параллелепипеда,
построенного на трех некомпланарных
векторах
![]() ,
,![]() ,
,![]() ,
взятому со знаком плюс, если тройка
векторов правая, и со знаком минус, если
эта тройка левая (рис. 19).
,
взятому со знаком плюс, если тройка
векторов правая, и со знаком минус, если
эта тройка левая (рис. 19).
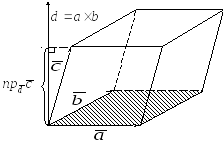
Рис. 19
Если
векторы
![]() ,
,![]() ,
,![]() заданы своими координатами,
заданы своими координатами,![]() ,
,![]() ,
,![]() ,то
смешанное
произведение
трех векторов
,то
смешанное
произведение
трех векторов
![]() ,
,![]() ,
,![]() равно определителю третьего порядка,
составленному из координат этих векторов:
равно определителю третьего порядка,
составленному из координат этих векторов:
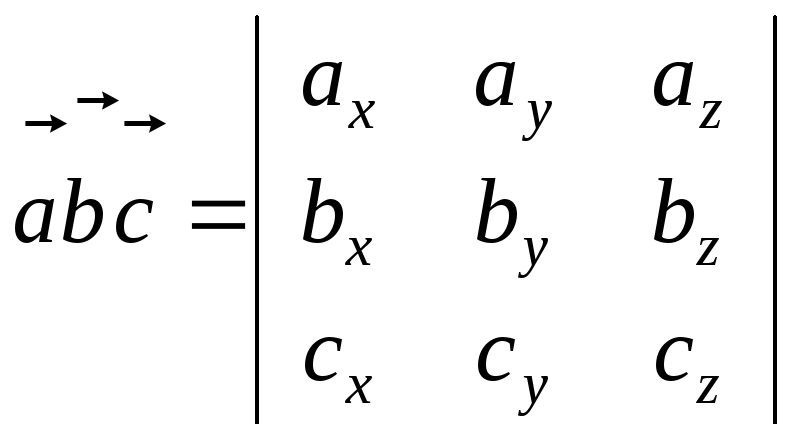 .
.
Векторы
![]() ,
,![]() ,
,![]() компланарны
тогда и только тогда, когда их смешанное
произведение равно нулю:
компланарны
тогда и только тогда, когда их смешанное
произведение равно нулю:
![]()
![]()
![]() = 0.
= 0.
Объем
параллелепипеда V,
построенного на трех некомпланарных
векторах
![]() ,
,![]() ,
,![]() ,
определяется по формуле:
,
определяется по формуле:
V
=
 .
.
Объем
тетраэдра,
построенного на трех некомпланарных
векторах
![]() ,
,![]() ,
,![]() ,
определяется по формуле:
,
определяется по формуле:
Vт
=
![]() =
=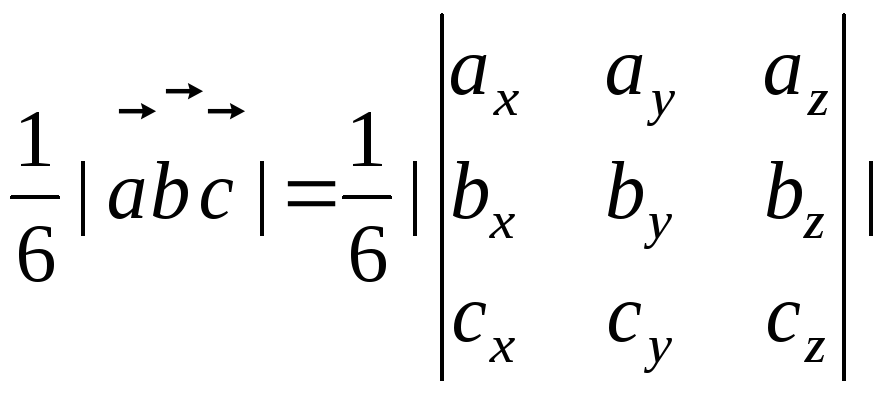 .
.
Пример 6. Даны вершины тетраэдра: А (2; 3; 1), В (4; 1; –2), С (6; 3; 7), D (–5; –4; 8). Необходимо найти:
1) площадь грани АВС;
2) объем тетраэдра АВСD;
3) длину высоты, опущенной на грань АВС;
4) внутренний угол А треугольника АВС.
Решение.
1. Если даны точки
М1(x1;
y1;
z1)
и М2(x2;
y2;
z2),
то вектор
![]() выражается следующим образом через
орты
выражается следующим образом через
орты![]() ,
,![]() ,
,![]() :
:
![]() =
(x2
– x1)
=
(x2
– x1)![]() +
(у2
– у1)
+
(у2
– у1)![]() +
(z2
– z1)
+
(z2
– z1)![]() .
.
Найдем векторы АВ, АС и АD в системе орт:
![]() =
(4 – 2)
=
(4 – 2)![]() +
(1 – 3)
+
(1 – 3)![]() +
(–2 – 1)
+
(–2 – 1)![]() =
2
=
2![]() –
2
–
2![]() –
3
–
3![]() ;
;
![]() =
(6 – 2)
=
(6 – 2)![]() +
(3 – 3)
+
(3 – 3)![]() +
(7 – 1)
+
(7 – 1)![]() =
4
=
4![]() + 6
+ 6![]() ;
;
![]() =
(–5 – 2)
=
(–5 – 2)![]() +
(–4 – 3)
+
(–4 – 3)![]() +
(8 – 1)
+
(8 – 1)![]() =
–7
=
–7![]() –
7
–
7![]() + 7
+ 7![]() .
.
Площадь грани АВС
равна половине площади параллелограмма,
построенного на векторах
![]() и
и![]() .
Площадь параллелограмма, в свою очередь,
численно равна модулю векторного
произведения векторов
.
Площадь параллелограмма, в свою очередь,
численно равна модулю векторного
произведения векторов![]() и
и![]() .
.
Найдем векторное
произведение векторов
![]() и
и![]() :
:
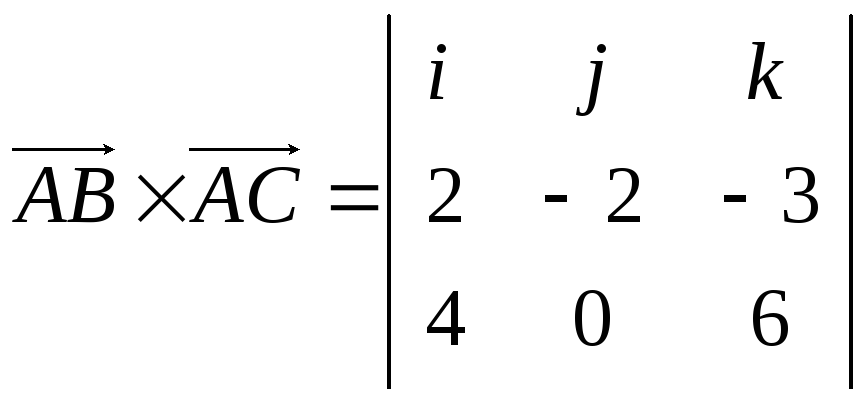 = (–2∙6 – 0∙(–3))
= (–2∙6 – 0∙(–3))![]() –
(2∙6– 4∙(–3))
–
(2∙6– 4∙(–3))![]() + (2∙0 – 4∙(–2))
+ (2∙0 – 4∙(–2))![]() =
=
= –12![]() –
24
–
24![]() + 8
+ 8![]() .
.
Найдем модуль векторного произведения
![]() =
=
![]() .
.
Тогда SАВС
=
![]()
![]() =
=![]() ∙ 28 = 14.
∙ 28 = 14.
2. Объем тетраэдра
равен
![]() объема параллелепипеда, построенного
на трех некомпланарных векторах
объема параллелепипеда, построенного
на трех некомпланарных векторах![]() ,
,![]() ,
,![]() .
Найдем объем параллелепипеда как модуль
смешанного произведения векторов
.
Найдем объем параллелепипеда как модуль
смешанного произведения векторов![]() ,
,![]() ,
,![]() :
:
![]() =
=
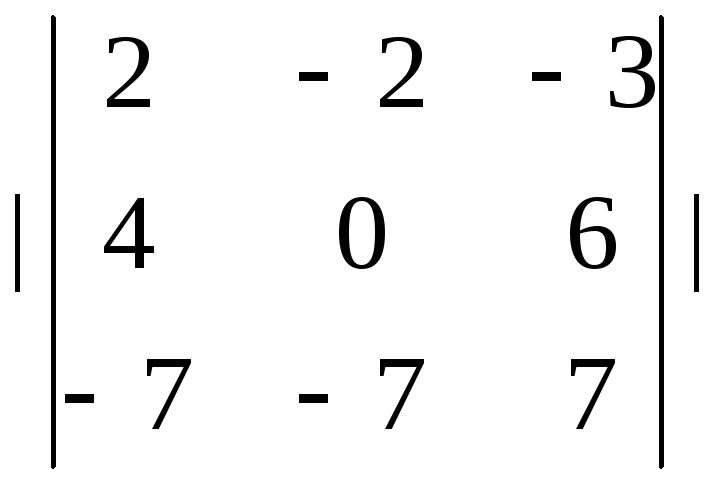 = 308.
= 308.
Тогда объем
тетраэдра VАВСD
=
![]() ∙
∙![]() =
=
![]() ∙ 308 =
∙ 308 =
![]() .
.
3. Из курса
элементарной геометрии известно, что
объем тетраэдра V
равен
![]() произведения площади основания S
на высоту H:
произведения площади основания S
на высоту H:
![]() .
.
Выразим высоту Н
из последнего уравнения: ![]() .
.
Подставляя
в эту формулу
![]() и S
=
SАВС
= 14, получим:
и S
=
SАВС
= 14, получим:
 .
.
4. Косинус угла ,
образованного векторами
![]() и
и![]() ,
равен их скалярному произведению,
делённому на произведение их модулей:
,
равен их скалярному произведению,
делённому на произведение их модулей:
cos
=
![]()
Найдем модули
(длины) векторов
![]() и
и![]() :
:
|![]() |
=
|
=![]() ;
;
|![]() |
=
|
=![]() .
.
Тогда cos
А
= cos
=
![]() .
.
А 109,65.
