1. Линейная алгебра

1.1. Системы линейных уравнений

Системой линейных алгебраических уравнений, содержащей m уравнений и n переменных, называется система вида:

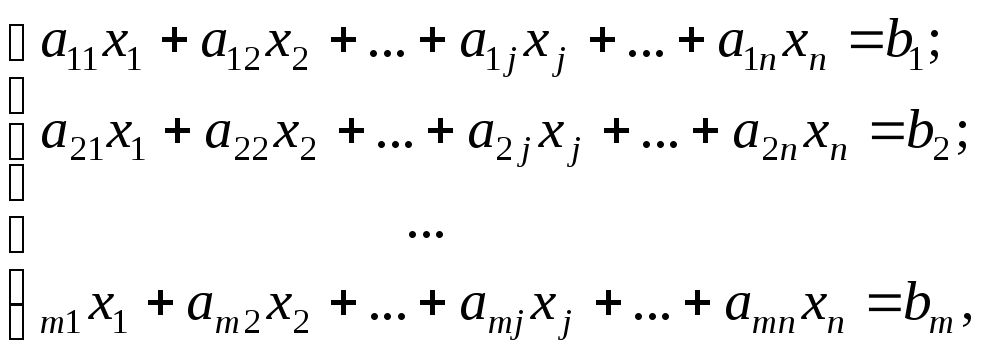
где числа а_ij, i = 1, 2,…, m, j = 1, 2, …, n, называются коэффициентами при переменных, числа b_i – свободными членами уравнений.

Систему можно записать в компактной матричной форме

А · Х = В,

где А – матрица коэффициентов при переменных; Х – матрица-столбец переменных; В – матрица-столбец свободных членов:

А = 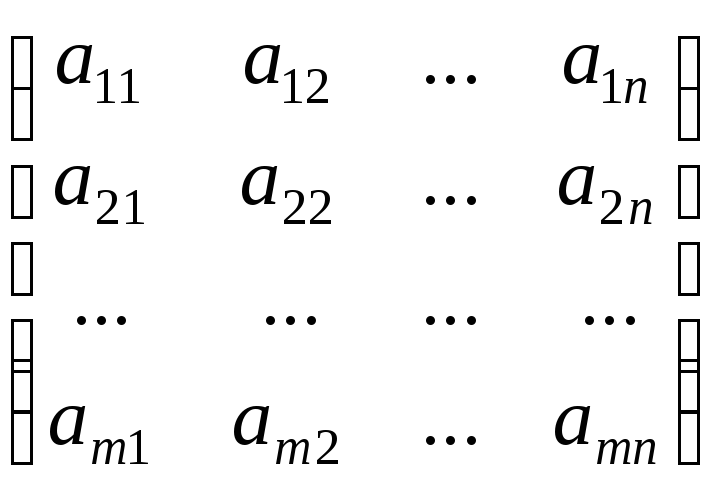,Х = ,В = .

Решением системы называется такая совокупность n чисел (х₁ = k₁, x₂ = k₂, …, x_n = k_n), при подстановке которых каждое уравнение системы обращается в верное равенство.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.

Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.

Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Эквивалентные системы получаются при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками.

К элементарным преобразованиям относятся следующие:

1) Умножение строки на число, отличное от нуля.

2) Прибавление к одной строке другой, умноженной на любое число.

3) Перемена местами двух строк.

Для нахождения решения системы линейных уравнений применяют метод Крамера, метод обратной матрицы и метод Гаусса.

1.2. Метод обратной матрицы

Пусть число уравнений системы равно числу переменных: т = п. Тогда матрица системы является квадратной. Ее определитель (А) называется определителем системы.

Для получения решения системы линейных уравнений при т = п в общем виде предположим, что квадратная матрица системы А невырожденная: ее определитель (А) ≠ 0. В этом случае существует обратная матрица А^-1.

Умножим обе части матричного равенства А Х = В на матрицу А^-1 слева. В результате получим такие соотношения:

А^–1 (АХ) = А^–1В;

А^–1 (АХ) = (А^–1А) Х = ЕХ = Х.

Следовательно, решением системы линейных уравнений методом обратной матрицы является матрица-столбец, равная произведению обратной матрицы А^-1 и матрицы свободных членов В:

Х = А^–1 В.

Отыскание решения системы по данной формуле называют матричным методом решения системы.

Пример 1. Решить систему линейных уравнений матричным методом

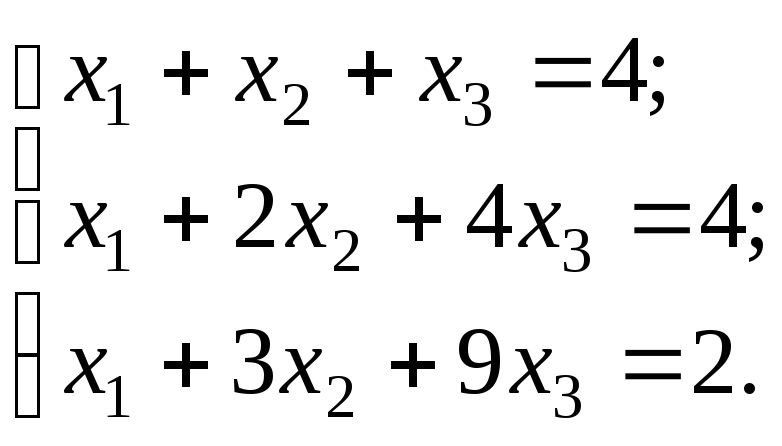
Решение.

Обозначим: А – матрица коэффициентов при переменных; Х – матрица-столбец переменных х₁, х₂, х₃; В – матрица-столбец свободных членов:

А = 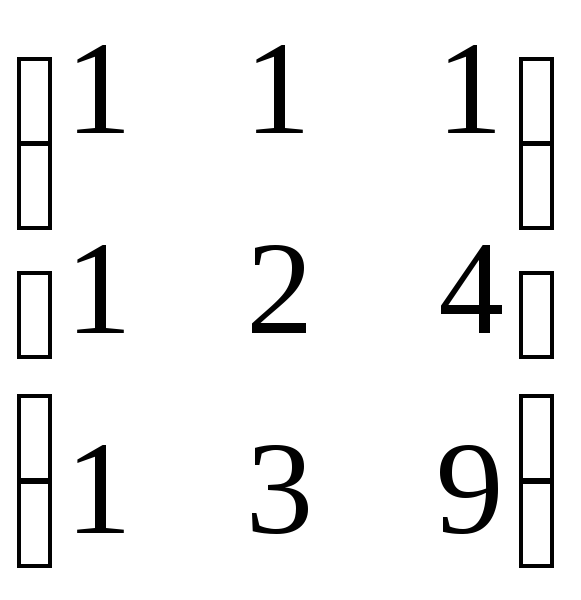,Х = ,В = .

Исходную систему уравнений запишем в матричном виде:

А · Х = В.

Решение системы будем искать в виде:

Х = А^–1 ·В.

Вычислим определитель матрицы А:

∆ = = 18 + 3 + 4 – 2 – 12 – 9 = 2 0.

Так как ∆  0, то матрица А имеет обратную матрицу А^–1.

Найдем транспонированную матрицу А^Т:

А^Т = .

Вычислим союзную матрицу А_с, составленную из алгебраических дополнений A_ij элементов матрицы А^Т:

А_с = =.

Запишем обратную матрицу А^–1:

А^–1 = =.

Найдем решение системы линейных уравнений в матричной форме:

Х = А^–1 · В = ∙=

= .

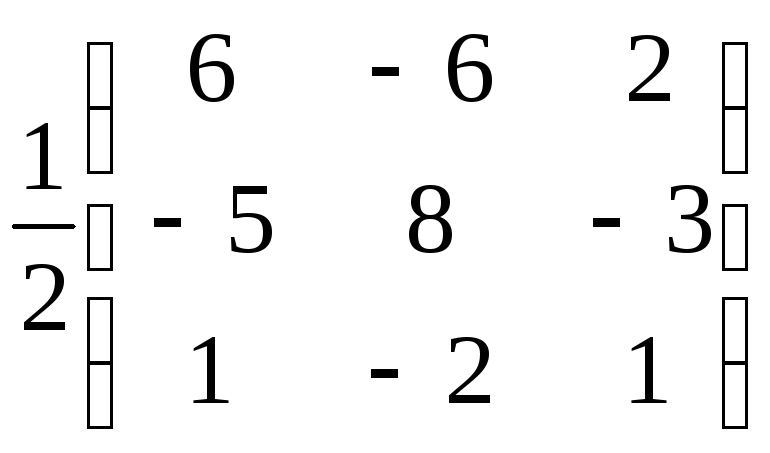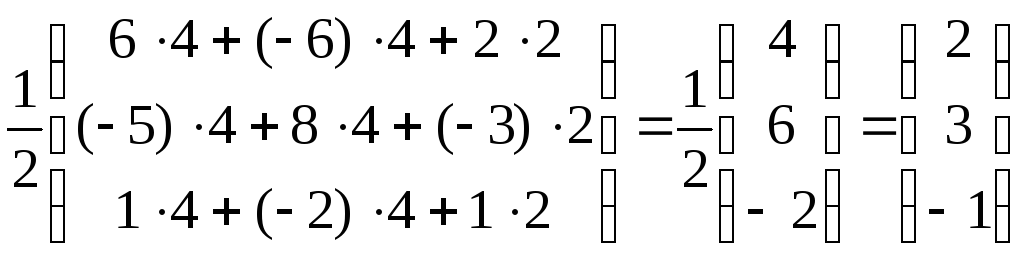Отсюда х₁ = 2, х₂ = 3, х₃ = –1.