4.2. Прямая в пространстве

Прямая в пространстве задается как линия пересечения двух непараллельных плоскостей общими уравнениями:

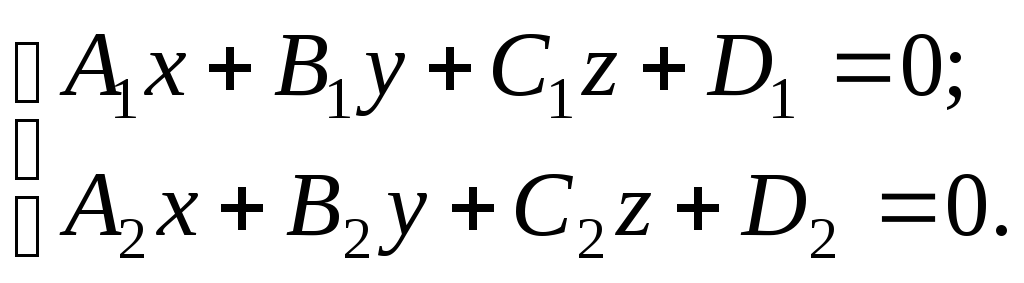
Прямая, проходящая через точку М(х₀; у₀; z₀) и параллельная направляющему вектору (l; m; n), определяется каноническими уравнениями:

.

Если в канонических уравнениях прямой l = 0, то прямая параллельна плоскости Оуz.

Если m = 0, то прямая параллельна плоскости Охz.

Если n = 0, то прямая параллельна плоскости Оху.

Если одновременно l = 0 и m = 0, то прямая параллельна оси Оz.

Если одновременно l = 0 и n = 0, то прямая параллельна оси Оу.

Если одновременно m = 0 и n = 0, то прямая параллельна оси Ох.

Параметрические уравнения прямой в пространстве имеют вид:

Здесь –  < t < + .

Уравнение прямой, проходящей через две данные точки М₁ (х₁; у₁; z₁) и

М₂ (х₂; у₂; z₂), имеет вид:

.

4.3. Прямая и плоскость в пространстве

Угол между плоскостьюАх+Ву+Сz+D = 0 ипрямой, заданной каноническими уравнениями, определяется по формуле:

.

Прямая и плоскость параллельны, еслиAl+Bm+Cn= 0.

Прямая и плоскостьперпендикулярны, если.

Прямая, проходящая через точкуМ(х₀;у₀;z₀) и перпендикулярная к плоскостиАх+Ву+Сz+D = 0, имеет направляющий вектор(А;В;С) и определяется уравнениями:

.

Расстояние от точкиМ₁(х₁;у₁;z₁) до прямой, определяется по формуле:

.

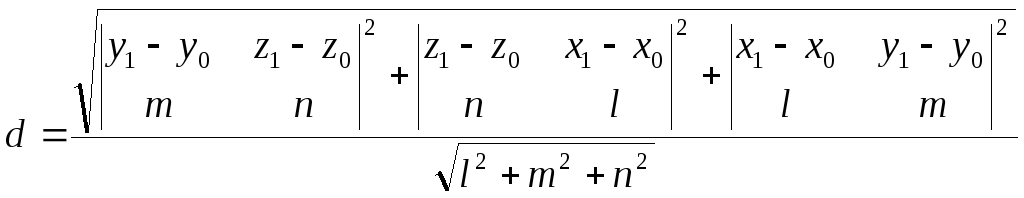Пример 7. Даны координаты четырех точек А(1; –1; 1), В(–2; 1; 3), С(4; –5; –2), D(–1; 1; –2). Необходимо найти:

1. уравнение плоскости Q, проходящей через точки А, В, С;

2. канонические уравнения прямой АВ;

3. уравнение плоскости G, проходящей через точку D перпендикулярно прямой АВ;

4) расстояние от точки D до плоскости Q.

Решение.

Уравнение плоскости, проходящей через три данные точки М₁ (х₁; у₁; z₁), М₂ (х₂; у₂; z₂), М₃ (х₃; у₃; z₃), имеет вид:

.

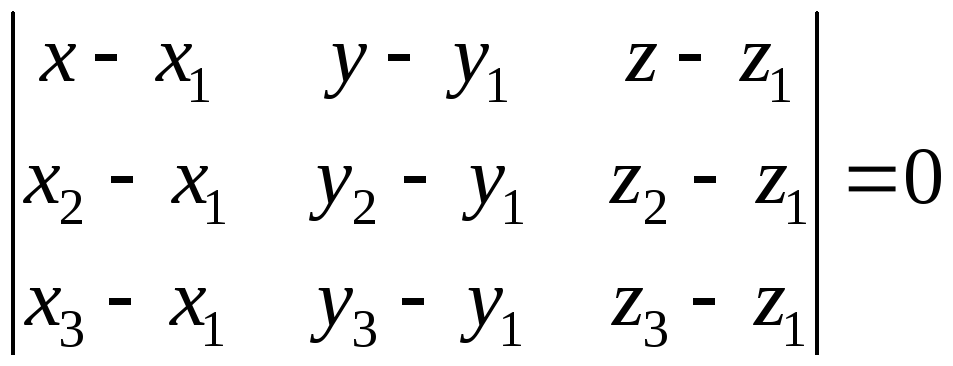Составим уравнение плоскости Q, проходящей через точки А, В, С:

.

Преобразуем уравнение плоскости, разложив определитель по первой строке:

; (х – 1)– (у + 1) + (z – 1)= 0;

2(х – 1) –3(у + 1) + 6(z – 1) = 0.

Тогда уравнение плоскости Q имеет вид: 2х – 3у + 6z – 11 = 0.

2. Уравнения прямой, проходящей через две данные точки А₁ (х₁; у₁; z₁), А₂ (х₂; у₂; z₂), определяется по формуле:

.

Подставляя координаты точек А(1; –1; 1) и В(–2; 1; 3), получим канонические уравнения прямой АВ:

или .

Направляющий вектор прямой АВ имеет координаты (–3; 2; –3).

3. Так как искомая плоскость G перпендикулярна прямой АВ, то вектор нормали плоскости параллелен направляющему вектору прямойАВ , т.е..

Уравнение плоскости, проходящей через точку М(х₀; у₀; z₀) перпендикулярно вектору нормали , имеет вид:

А(х – х₀) + В(у – у₀) + С(z – z₀) = 0.

Подставляя в это уравнение вместо коэффициентов А, В, С пропорциональные им числа –3; 2; –3 и координаты точки D (–1; 1; –2), получим уравнение плоскости, перпендикулярной прямой АВ:

–3(х – (–1)) + 2(у – 1) + (–3)(z – (–2)) = 0.

Преобразуем данное уравнение:

–3(х + 1) + 2(у – 1) –3(z + 2) = 0; –3х + 2у – 3z – 11 = 0 (плоскость G).

4. Расстояние от точки М(х₀; у₀; z₀) до плоскости Q Ах + Ву + С + D = 0 определяется по формуле:

.

Подставляя координаты точки D (–1; 1; –2) и коэффициенты общего уравнения плоскости Q 2х –3у + 6z – 11 = 0, найдем расстояние от точки до плоскости:

= 4.