Вопросы

1. Какие задачи называются метрическими ?

2. Какие задачи относятся к метрическим?

3. Какими методами можно определить натуральную величину отрезка?

4. Какие преобразования необходимо выполнить для преобразования плоскости общего положения в проецирующую?

5. В чем суть метода прямоугольного треугольника?

Тесты к теме «Метрические задачи»

1.В каком случае прямой угол проецируется без искажения

а) во всех случаях проецирования

б) если одна из его сторон параллельна плоскости проекций, а другая ей не перпендикулярна

в) если одна из ее сторон перпендикулярна плоскости

2. Сколько преобразований необходимо выполнить для определения натуральной величины отрезка (методом замены плоскостей проекции).

а) одна

б) две

в)три

3. В какое положение необходимо преобразовать две пересекающиеся плоскости, чтобы определить угол между ними

а) в проецирующее

б) в общее положение

в) в параллельное плоскостям

4. Сколько преобразований необходимо выполнить для преобразования прямой общего положения в проецирующую прямую (методом замены плоскостей проекции).

а) одна

б) две

в) три

5. Как нужно расположить новую плоскость проекций, чтобы плоскость общего положения стала проецирующей

а) параллельно

б) перпендикулярно

в) под углом 45⁰

Перпендикулярность

Из решения задачи о нахождении натуральной величины отрезка прямой уровня следует, что плоская фигура или угол (образуемый двумя сторонами фигуры) проецируются на плоскость без искажения, если их плоскость и плоскость проекций параллельны (исключение составляет прямой угол).

Теорема о проецировании прямого угла формулируется так: если одна из сторон прямого угла параллельна какой-либо плоскости проекций, то на эту плоскость проекций прямой угол проецируется без искажения.

Перпендикулярность двух прямых. Допустим, что через точку М нужно провести прямую, перпендикулярную отрезку [АВ]. Сколько возможно решений, и какими они могут быть (рис. 35)?

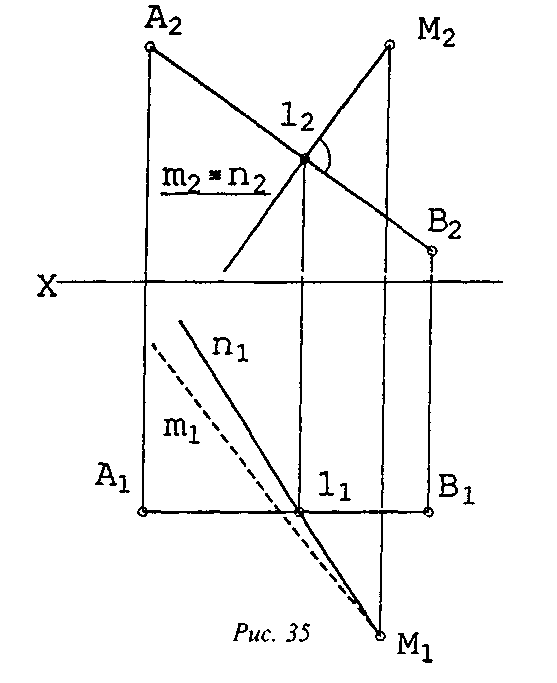
Заметим, что прямая (АВ) - фронталь. На основании сформулированной теоремы на фронтальной плоскости проекций можно из точки М₂ провести прямую n₂, перпендикулярную А₂В₂.

Есть два варианта решения рассматриваемой задачи (в зависимости от того, как расположены прямые n и (АВ) по отношению одна к другой).

1. Если n и (АВ) пересекаются, 1₂ - фронтальная проекция точки их пересечения 1. Горизонтальную проекцию (1₁) точки 1 можно найти по принадлежности к прямой (АВ), тем самым определив единственное положение прямой n (т.е., задача имеет одно решение).

2. Если n и (АВ) скрещиваются, общих точек они не имеют. Все прямые, скрещивающиеся с (АВ) под прямым углом, будут располагаться в плоскости, проходящей через точку М и перпендикулярной отрезку [АВ]. Поскольку через точку в плоскости можно провести бесконечное множество прямых, решений окажется бесконечно много. На комплексном чертеже все фронтальные проекции таких прямых совпадут с n₂, а горизонтальные отобразятся пучком прямых, проходящих через точку М₁ (на рис. 35 одна из подобных прямых, m₁, показана пунктиром).

Перпендикулярность прямой и плоскости. Общий геометрический признак перпендикулярности прямой и плоскости устанавливает, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости. Применительно к “Начертательной геометрии” отмеченный признак формулируется так: прямая перпендикулярна плоскости, если проекции прямой перпендикулярны одноименным проекциям прямых уровня этой плоскости.

Проиллюстрируем приведенные соображения на примере решения следующей задачи. Пусть плоскость Σ задана параллельными прямыми а и b. Из точки М требуется опустить на эту плоскость перпендикуляр m (рис. 36).

Использование теоремы о частном случае проецирования прямого угла позволяет предложить такой алгоритм решения:

1. В плоскости Σ в любом месте строятся ее фронталь и горизонталь.

2. Через точки М₁ и М₂ проводятся перпендикуляры к h₁ и f₂ (к горизонтальной проекции горизонтали и фронтальной проекции фронтали).

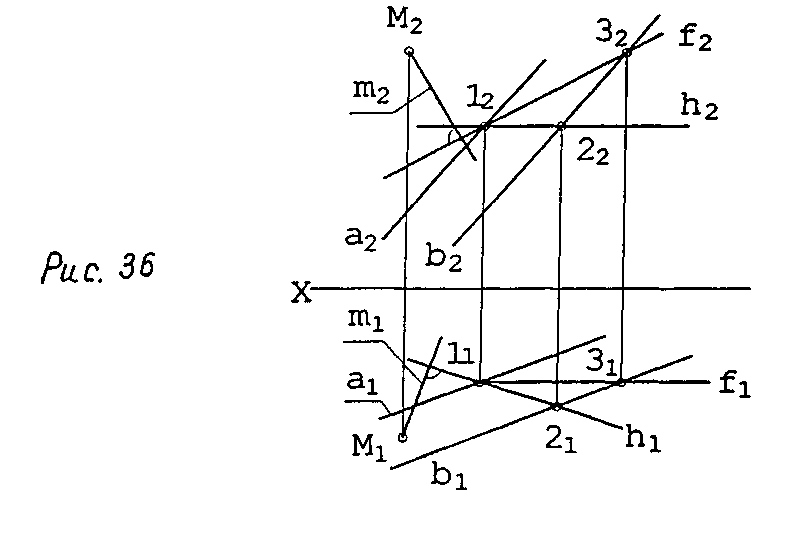
3. Нужно заметить, что точка пересечения прямой и плоскости не найдена, но это и не требовалось по условию задачи.

Чтобы лучше представить процесс решения, следует подчеркнуть, что указанная точка в общем случае не будет располагаться в месте пересечения проведенных фронтали и горизонтали плоскости. Если из точки пересечения упомянутых линий уровня восставить к .плоскости перпендикуляр, все перпендикуляры к плоскости, проведенные из любой точки, окажутся ему параллельны.

При решении многих задач о перпендикулярности прямой и плоскости надо принимать во внимание обстоятельство, что плоскость и перпендикуляр к ней представляют собой своеобразную “жесткую” систему. Если плоскость является плоскостью общего положения, то и перпендикуляр к ней - прямая общего положения. Когда плоскость - частного положения, перпендикуляр к ней - прямая частного положения.

Перпендикулярность двух плоскостей. Признак перпендикулярности плоскостей утверждает, что плоскость Σ перпендикулярна плоскости Ω, если плоскость Σ проходит через прямую, перпендикулярную плоскости Ω.

Представление решений многих задач на комплексном чертеже облегчает следующий факт: если плоскости Σ и Ω перпендикулярны, перпендикулярны и соответствующие проекции их прямых уровня.