Вопросы

1. Понятие принадлежности точки прямой.

2. Понятие принадлежности прямой поверхности.

Параллельность прямой и плоскости. Параллельнлсть плоскостей.

Общий признак параллельности прямой и плоскости формулируется следующим образом: прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости. Отсюда вытекает общий признак параллельности плоскостей - если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой, плоскости параллельны между собой.

Практическое применение отмеченных соображений рассмотрим на примерах решения двух задач.

Задача 1. Через точку К провести плоскость, параллельную прямой m (рис.20).

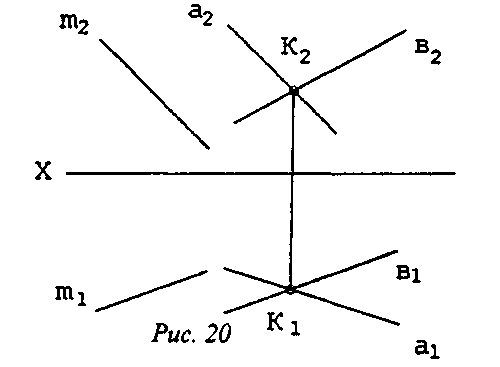
Коротко решение описывается так. Даны плоскость m (m₁; m₂) и точка К (K₁; K₂). Чтобы провести через К некую плоскость Σ, параллельную прямой т, достаточно изобразить на комплексном чертеже проходящие через точку К фронтальную а₂ и горизонтальную a₁ проекции прямой а, параллельные соответствующим проекциям заданной прямой m, а далее провести через К произвольную прямую b (решений - бесконечное множество).

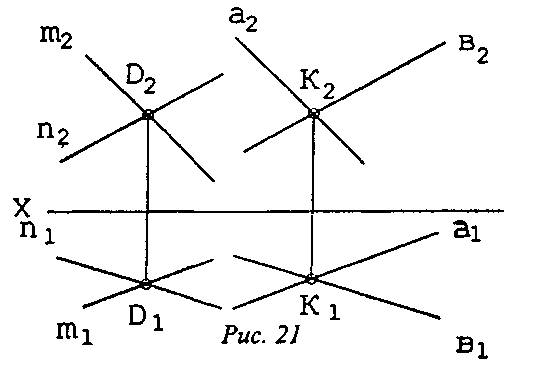
Задача 2. Через точку К провести плоскость Σ, параллельную плоскости Г, заданной двумя пересекающимися прямыми n и m(рис.21).

Вопросы

1. Условие параллельности прямой и плоскости.

2. Условие параллельности двух плоскостей.

По условию плоскость Г задана на комплексном чертеже проекциями двух пересекающихся прямых (m (m₁; m₂), n (n₁; n₂)), а точка К - двумя своими проекциями (К (К₁; К₂)). Чтобы решить поставленную задачу, через точку К достаточно провести пересекающиеся прямые а и b, соответствующие проекции которых параллельны проекциям прямых mиn (решение - единственное).

Тесты к теме «Параллельность прямой и плоскости. Параллельность плоскостей».

1. Условие параллельности прямой и плоскости

а) прямая параллельна плоскости если она параллельна какой-либо прямой, лежащей в этой плоскости.

б) прямая параллельны плоскости, если она перпендикулярна прямой лежащей в этой плоскости

в) прямая параллельна плоскости, если она параллельна двум прямым, лежащим в этой плоскости.

2.Условие параллельности плоскостей

а) две плоскости параллельны друг другу, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости

б) две плоскости параллельны друг другу если, две пересекающиеся прямые одной плоскости перпендикулярны двум пересекающимся прямым другой плоскости

в) две плоскости параллельны, если в плоскости имеется прямая параллельная плоскости

Главные позиционные задачи

Решение значительного числа практических задач связано с вопросами пересечения геометрических образов (тел). Ввиду их особой важности, задачи о пересечении называют главными позиционными (ГПЗ), различая два их типа: 1-я (пересечение линий с поверхностями) и 2-я (пересечение поверхностей) ГПЗ.

Отмеченное о двух видах ГПЗ характеризует общее для каждого из них, подразумевая, что понятие каждого из компонентов пересечения (линия, поверхность) включает в себя все вероятные его варианты. Так, к 1-й ГПЗ относятся пересечения прямой и плоскости, прямой и поверхности, кривой и плоскости, кривой и поверхности, а ко 2-й - плоскостей, плоскости и поверхности, поверхностей.

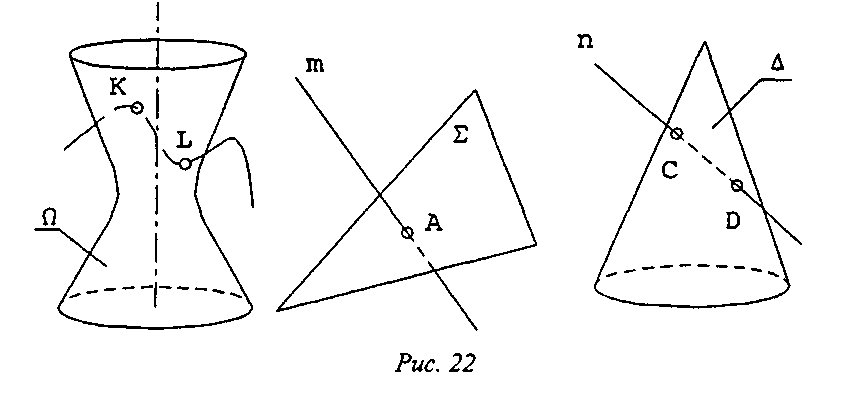
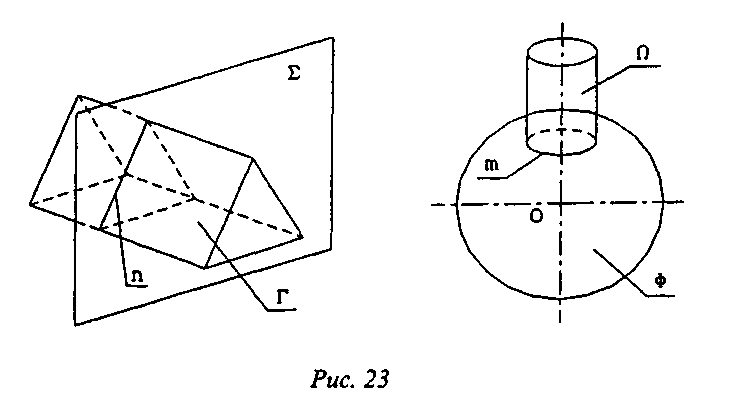
Решение любой задачи на пересечение состоит в определении общего элемента двух геометрических образов (искомого геометрического образа). Очевидно, что в 1-й ГПЗ им является точка или несколько (конечное число) точек (рис. 22). Во 2-й ГПЗ искомым геометрическим образом служит линия (рис. 23).

Искомый геометрический образ как результат пересечения заданных геометрических образов всегда принадлежит им одновременно и может быть определен либо прямо, на основании свойств пересекающихся образов, либо через посредство свойств некоего нового геометрического образа (их совокупность).

Методика решения ГПЗ предполагает использование проецирующих свойств геометрических образов. Поскольку подобные образы бывают как проецирующие, так и нет, и для 1-й, и для 2-й ГПЗ при всем многообразии вариантов существует три случая пересечения.

Случай 1. Оба пересекающихся геометрических образа проецирующего характера.

Случай 2. Один из пересекающихся образов проецирующий, а второй -нет.

Случай 3. Оба пересекающихся образа непроецирующего характера.

Определение главной проекции геометрического образа, приведенное выше, позволяет утверждать, что в первом случае непосредственно на чертеже можно указать обе проекции искомого геометрического образа, во втором -одну его проекцию, а в третьем определение проекций искомого образа требует использования некоего нового геометрического образа-посредника, обладающего проецирующими свойствами.

Отмеченные соображения основаны на том, что точка, линия, фигура, принадлежащие проецирующему геометрическому образу, обладают одноименными проекциями, совпадающими с его главной проекцией. Это дает возможность не просто систематизировать все вероятные случаи пересечения, но и алгоритмизировать сам процесс решения ГПЗ.

Чтобы показать общее в решениях задач на пересечение и пояснить их алгоритмы для того или иного случая пересечения, рассмотрим ряд примеров.

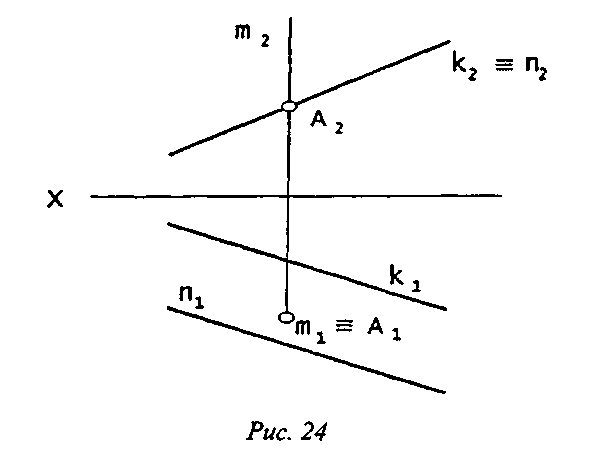
Задача 1. Горизонтально-проецирующая прямая m задана своими проекциями (m₁; m₂), а фронтально-проецирующая плоскость Σ – двумя параллельными прямыми n и k. Требуется определить А - точку пересечения прямой m и плоскости Σ.

Решение приведено на рис. 24. Кратко его ход можно пояснить следующим образом. Поскольку (по условию) искомая точка А принадлежит одновременно и прямой m, и плоскости Σ, то проекции точки принадлежат соответствующим проекциям прямой и плоскости. Т.к. прямая m является горизонтально проецирующей, то горизонтальные проекции прямой и точки (m₁ и a₁) совпадают. Но плоскость Σ - фронтально-проецирующая; поэтому

вторая проекция искомой точки (А₂) определяется пересечением фронтальных проекций прямых m и n(k) – m ₂ и n ₂ (k ₂).

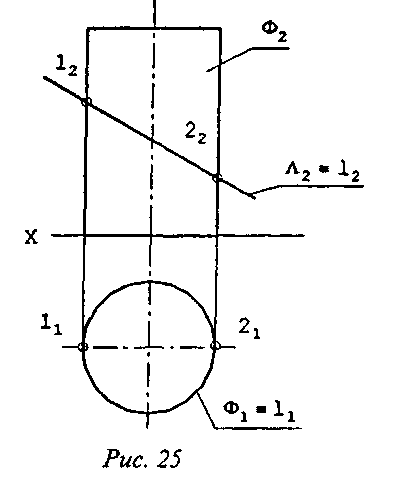
Задача 2. Заданы фронтально-проецирующая плоскость Λ (Λ₂) и цилиндрическая поверхность Ф(Ф₁; Ф₂). Необходимо отыскать 1 - линию пересечения плоскости Λ с поверхностью Ф.

Решение показано на рис. 25. По определению искомая линия пересечения принадлежит одновременно и плоскости Λ, и поверхности Ф, т.е. проекции этой линии принадлежат соответствующим проекциям и плоскости, и поверхности. Поскольку плоскость Λ является фронтально-проецирующей, фронтальная проекция искомой линии пересечения (1₂)совпадает с

фронтальной проекцией самой плоскости (Λ ₂). Заметим, что поверхность Ф является горизонтально проецирующим геометрическим образом. Отсюда следует, что горизонтальные проекции искомой линии пересечения и заданной поверхности (l₁ и Ф₁) совпадают.

Замечание. При рассмотрении интервала существования 1 необходимо помнить, что общность искомого геометрического образа определяет граница его существования в пределах общей принадлежности к заданным образам (в рассмотренном примере она определена точками 1 и 2).

Приведенная задача 1 относится к 1-й ГПЗ, а 2 - ко 2-й. В обоих случаях требовалось найти пересечение проецирующих геометрических образов (первый случай пересечения), а методика решения задач практически одинакова. Это означает, что для указанного случая пересечения существует общий для 1-й и 2-й ГПЗ алгоритм решения:

1. Обе проекции искомого общего геометрического образа уже заданы на чертеже при постановке условия задачи.

2. Эти проекции принадлежат главным проекциям проецирующих

образов в пределах общности заданных геометрических образов.

3. Решение задачи фактически сводится к простановке обозначений проекций искомого общего геометрического образа на чертеже.

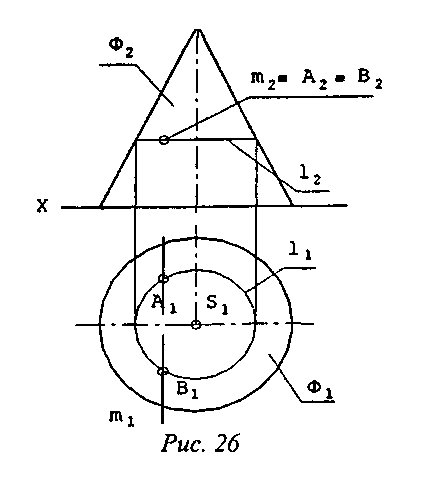
Задача 3. Заданы фронтально-проецирующая прямая m(m₁; m₂) и коническая поверхность Ф(Ф₁; Ф₂). Определить А и В - точки пересечения прямой с поверхностью.

Решение показано на рис. 26. Т.к. искомые точки А и В принадлежат одновременно и прямой m, и поверхности Ф, то и проекции этих точек (А₁; Bj; А₂ и B₂) принадлежат соответствующим проекциям прямой и поверхности. Поскольку по условию прямая m является фронтально-проецирующей, фронтальные проекции ее и искомых точек (m₂, А₂ и B₂) совпадают. Но искомые точки А и В по определению лежат на некоей линии 1, принадлежащей поверхности Ф, т.е. их горизонтальные проекции принадлежат горизонтальной проекции 1 (l₁). Одновременно А и В лежат на прямой m. Очевидно, что

горизонтальные проекции искомых точек (А₁ и В₁) определяются пересечением горизонтальных проекций прямой m и линии 1 (m₁ и l₁).

Анализ условия решенной задачи показывает, что она относится к 1-й ГПЗ для случая 2.

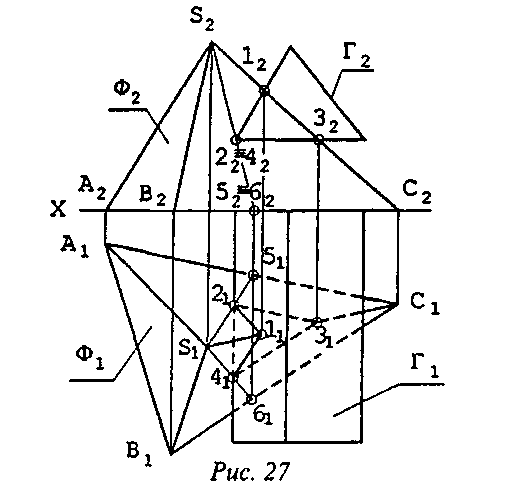
Задача 4. Своими проекциями заданы поверхности Г (прямая призма) и Ф (треугольная пирамида). Нужно найти k - линию пересечения поверхностей (рис. 27).

Решение. Поскольку искомая линия k одновременно принадлежит обеим поверхностям, то ее проекции принадлежат соответствующим проекциям заданных поверхностей. Призма Г является фронтально-проецирующим геометрическим образом. Поэтому фронтальная проекция искомой линии пересечения ^) совпадает с фронтальной (Г₂) проекцией призмы (контур 1₂-2₂≡4₂-3₂ на плоскости П₂)- Чтобы найти горизонтальную проекцию искомой линии пересечения (k₁), достаточно определить горизонтальные проекции точек 1,2,3 и 4 (l₁, 2₁, 3₁ и 4₁) и соединить их отрезками (нужно напомнить, что видимость геометрических образов определяется с помощью метода конкурирующих точек). Очевидно, что точки 1 и 3 принадлежат ребру пирамиды [SC]. Горизонтальные проекции этих точек легко найти, используя соответствующие линии связи (рис. 27). Аналогично определяется положение горизонтальных проекций точек 2 и 4, принадлежащих одновременно призме и граням пирамиды ASC и BSC соответственно, но для нахождения проекций 2₁ и 4₁ предварительно требуется произвести дополнительные геометрические построения (отрезки [S5] и [S6], принадлежащие граням пирамиды ASC и BSC и проходящие через точки 2 и 4; фронтальные проекции этих отрезков совпадают).

Решенная задача относится ко 2-й ГПЗ для второго случая пересечения.

Примеры 3 и 4 позволяют сформулировать алгоритм решения задач для второго случая пересечения:

1. Одна проекция искомого геометрического образа непосредственно задана на чертеже и принадлежит главной проекции проецирующего образа в пределах ее общности с заданным непроецирующим образом.

2. Вторая проекция искомого образа определяется по принадлежности к заданному непроецирующему образу.

Задача 5. Заданы прямая m и плоскость Σ (двумя пересекающимися прямыми а и b) общего положения. Найти М - точку их пересечения (рис. 28).

Прежде, чем записать решение этой задачи, попробуем предложить следующий алгоритм решения 1-й ГПЗ для случая 3:

1. Через заданную прямую нужно провести проецирующую плоскость-посредник.

2. Далее необходимо построить линию пересечения заданной плоскости и плоскости-посредника (второй случай пересечения!).

3. Надо определить точку пересечения заданной прямой и построенной линии пересечения, которая и окажется искомым геометрическим образом.

Такие же соображения можно сформулировать и в случае, когда нужно найти линию пересечения, а в качестве посредников выбраны некоторые поверхности. Сама искомая линия будет представлена совокупностью точек.

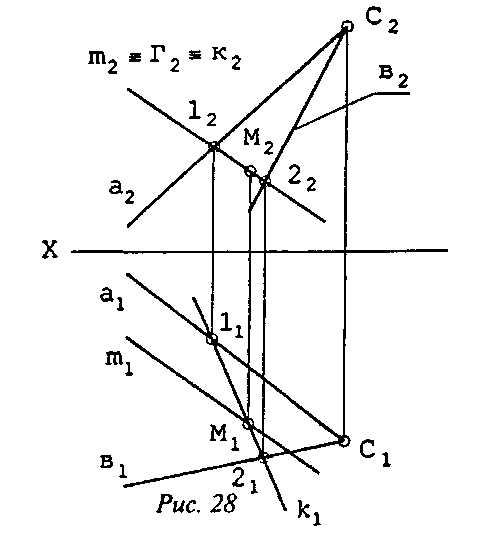
Решение. Итак, прямая m задана своими проекциями (m(m₁; m₂)), а плоскость Σ - двумя пересекающимися прямыми а и b (а(а₁; a₂) и b(b₁; b₂)).

Чтобы найти искомую точку М пересечения прямой и плоскости, проведем через m фронтально-проецирующую плоскость Г. Отметим, что фронтальные проекции m, Г и некоторой прямой k, лежащей в плоскости Г, совпадают. Без труда можно определить фронтальные проекции точек 1 и 2 пересечения k с а и b соответственно (1₂ и 2₂), найти с помощью линий связи горизонтальные проекции этих точек (l₁ и 2₁) и построить k₁ - горизонтальную проекцию k, фактически, линии пересечения заданной плоскости и плоскости-посредника. Пересечение проекций m₁ и k₁ определяет горизонтальную проекцию искомой точки M (M₁). Осталось провести линию связи и найти фронтальную

проекцию точки М.

Надо подчеркнуть, что посредник мог быть выбран другим, но в рассмотренном случае проецирующее свойство посредника позволило использовать алгоритм решения для второго случая пересечения, упростив задачу. Разберем еще один пример.

Задача 6. Даны две плоскости общего положения: плоскость Г задана параллельными прямыми а и b, плоскость Σ - пересекающимися прямыми c и d. Найти к - линию пересечения этих плоскостей.

Прежде, чем записать решение задачи, наметим его алгоритм, который можно рекомендовать при решении любой 2-й ГПЗ для случая пересечения 3.

1. Обе заданные поверхности следует пересечь некими посредниками (плоскостями или поверхностями).

2. Необходимо построить линии пересечения каждой из заданных плоскостей (поверхностей) с посредниками.

3. Далее нужно найти точки пересечения построенных линий.

4. Действия 1...3 требуется повторить столько раз, сколько необходимо найти точек для построения искомой линии пересечения.

5. Наконец, определенные точки нужно последовательно соединить в линию, которая и явится искомой линией пересечения.

Решение. С целью экономии места приведем вариант записи решения в пространстве, что позволяет более коротко проиллюстрировать как суть вспомогательных построений, так и предложенный выше алгоритм (рис. 29).

Очевидно, что для построения линии пересечения плоскостей - прямой -необходимо и достаточно определить две ее точки. Следовательно, решая поставленную задачу, нужно использовать две плоскости-посредника. В качестве таковых рационально выбрать фронтально-проецирующие плоскости Λ и Ω. Первая из них пересекается с заданными плоскостями Г и Σ по прямым r и р соответственно, а вторая - по прямым m и n. На пересечении прямых r и р лежит точка N, a m и n - точка М. Указанные точки определяют прямую k -искомую линию пересечения двух заданных плоскостей общего положения.

Решение дополнительно проиллюстрировано на рис. 30.

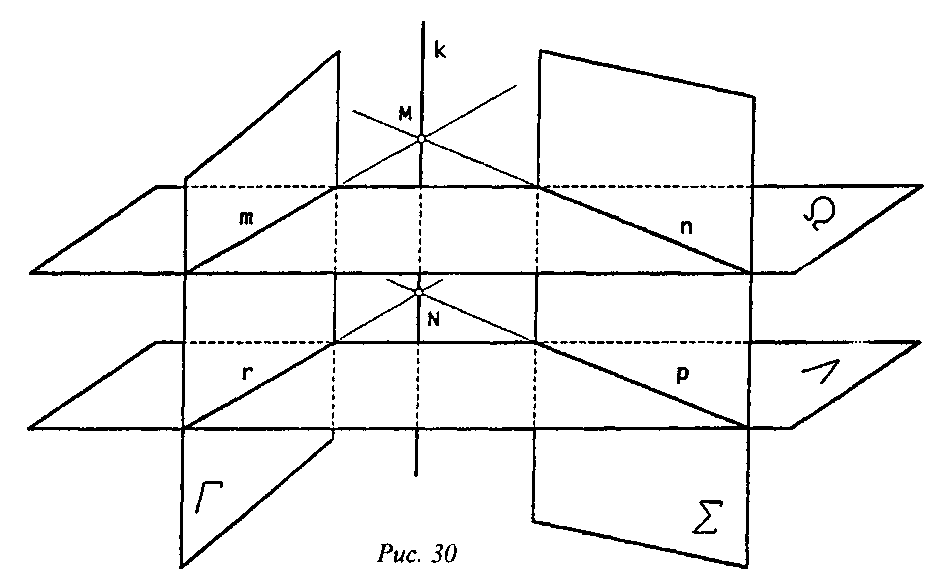
Необходимо подчеркнуть, что построение каждой из линий (r, р, m и n) фактически является решением задачи на второй случай пересечения, т.е. решение 2-й ГПЗ для третьего случая пересечения свелось к решению четырех задач на случай пересечения 2.

Помимо поясненного, существует еще один способ определения линии пересечения двух поверхностей общего положения, который часто применяют, когда требуется найти линию пересечения плоскостей, плоскости и поверхности, линейчатых поверхностей, из которых одна - гранная. Согласно ему следует выделить на одном из заданных геометрических образов прямые линии (по числу необходимых для построения линии пересечения точек), найти точки пересечения выделенных прямых с другим заданным геометрическим образом и последовательно соединить полученные точки в некую линию, которая и окажется искомой линией пересечения.

Например, в задаче о пересечении двух плоскостей общего положения, заданных (рис. 31) треугольниками ABC (плоскость Ω) и DEF (плоскость Λ), алгоритм решения в пространстве можно представить так: плоскость Ω задана двумя пересекающимися прямыми (АС) и (ВС), пересекающими плоскость Λ точках М и N соответственно (чтобы их найти, требуется решить 1-ю ГПЗ для случая 3); указанные точки определяют k - искомую линию пересечения.

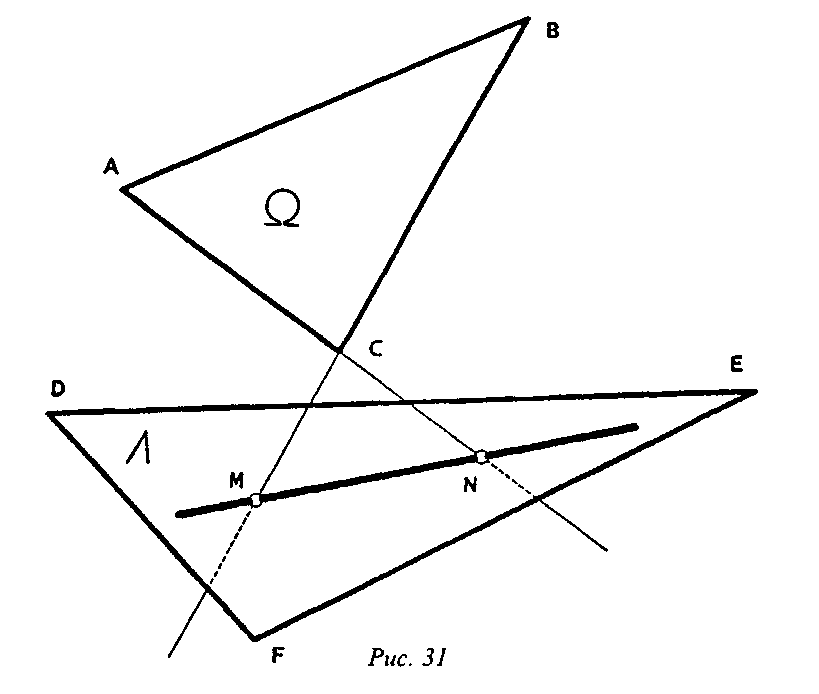
При подобном подходе решение 2-й ГПЗ для третьего случая пересечения сводится к решению двух 1 -х ГПЗ для случая 3 (нахождение линии (MN) - к определению положения точек М и N).

Нужно обратить внимание: в случае, когда обе пересекающиеся поверхности являются поверхностями вращения, оси которых пересекаются в одной точке, а плоскость, образованная осями вращения, параллельна какой-либо плоскости проекций, в качестве посредников целесообразно использовать сферические поверхности с общим центром в точке пересечения осей заданных поверхностей (способ сфер-посредников).