§25. Розподіл молекул за швидкостями

У попередніх параграфах підкреслювалася безладність, або хаотичність молекулярних рухів. Проте в 1860 році англійський фізик Дж. Максвелл, виходячи з основних положень молекулярно-кінетичної теорії, вивів точний закон, якому підпорядковані швидкості молекул газоподібного тіла (причому передбачається, що усі молекули газу однакові і що температура в усіх частинах газу також однакова). Розподіл молекул газу за швидкостями представлено на рисунку 2.31. По осі абсцис відкладаються різні значення швидкості молекул газу від нуля до деякої максимальної величини, а по осі ординат - відносне число молекул, швидкості яких лежать в інтервалі від v до v + Δv. Це число дорівнює площі виділеного на рисунку 2.31 стовпчика.

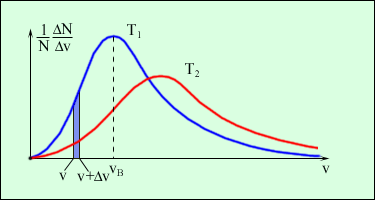
Рисунок 2.31.

Розподіл молекул за швидкостями. T₂ > T₁.

З графіку розподілу молекул за швидкостями виходить:

1. Число молекул, що мають малі швидкості дуже мале по відношенню до усього числа молекул газу.

2. Дуже мало також кількість молекул, що мають дуже великі швидкості.

3. Є одне значення швидкості, яке зустрічається частіше за інші значення, так звана найбільш ймовірна швидкість. v_йм. Цьому значенню відповідає максимум кривої розподілу.

4. Великий відсоток усіх молекул мають швидкості, що не дуже сильно відрізняється від найбільш ймовірної швидкості, тому в деяких спрощених розрахунках можна приймати, що усі молекули мають приблизно одну і ту ж швидкість.

Аналітично закон розподілу молекул за швидкостями виражається формулою:

(2.13)

де f(v) - функція розподілу, N - загальне число молекул у заданій масі газу, dN - число молекул, швидкості яких лежать в інтервалі від v до v + Δv, А - величина, яка залежить від температури газу і маси молекули.

На рисунку 2.31. показано дві криві розподілу швидкостей при різних температурах. Червона, більш полога крива, показує розподіл швидкостей за законом Максвелла при вищій температурі, ніж температура, до якої відноситься перша (синя) крива. Зіставлення цих двох кривих наочно виявляє властивості рівняння Максвелла. Видно, що при підвищенні температури росте найбільш ймовірна швидкість (максимум кривий розподіли зрушується направо); це відповідає тій обставині, що при підвищенні температури швидкості молекул зростають. Крива Максвелла при підвищенні температурі стає біль пологою: це означає, що при підвищенні температури розподіл молекул за швидкостями стає більш рівномірним.

Швидкість, при якій функція розподілу максимальна, називається найбільш ймовірною швидкістю. Її значення можна знайти, про диференціювавши функцію розподілу по змінній v і прирівнявши результат до нуля.

.

Використовуючи вираз , і вираз ,

отримаємо значення середньої квадратичної швидкості:

. (2.14)

Середня швидкість молекул (середня арифметична швидкість) визначається по формулі

.

(2.15)

Виходячи із співвідношень найбільш ймовірної, середньої квадратичної і середньої арифметичної швидкостей можна записати співвідношення:

v_cр ≈ 0,92 v_cр.кв. v_йм ≈ 0,815 v_cр.кв.

У таблиці 2.1 представлений розподіл за швидкостями молекул азоту при кімнатній температурі.

Таблиця 2.1

Область швидкостей м/с	Відсоток загального числа молекул, що мають швидкості, що знаходяться у вказаних інтервалах
0 0 <v <100	1
100 <v <300	25
300 <v <500	42
500 <v <700	24
700 <v <900	7
900 <v ..	1