4.2. Корневые критерии качества

Эта группа критериев базируется на оценке качества переходных процессов по значению полюсов и нулей передаточной функции системы, путем анализа корней ее знаменателя и числителя.

Передаточная функция системы связывает изображение выходной и входной величин зависимостью:

,

(4.6)

где ,.

Разложив многочлены в числителе и знаменателе на множители, передаточную функцию системы можно представить в виде:

,

(4.7)

где - нули передаточной функции,- полюсы передаточной функции.

Нули и полюсы передаточной функции определяют качественные показатели переходного процесса [3].

В частном случае, когда передаточная функция не имеет нулей:

,

(4.8)

качество переходного процесса определяется только полюсами передаточной функции.

Из теории линейных дифференциальных уравнений известно, что общее решение уравнения (4.8) имеет вид:

,

(4.9)

где - константа, зависящая от начальных условий;- корни знаменателя уравнения (4.8).

Таким образом, переходной процесс представляет собой сумму составляющих, число которых определяется числом корней характеристического уравнения, т.е. порядком уравнения системы.

Уравнение–ой степени содержит корней. В общем случае

,

(4.10)

Корни могут быть вещественными, комплексными попарно–сопряжёнными, мнимыми попарно–сопряжёнными и нулевыми.

Принято по расположению на комплексной плоскости корни называть левыми, если и правыми, если .

Условие устойчивости формулируется так: для асимптотической устойчивости линейной системы необходимо и достаточно, чтобы все корни её характеристического уравнения были левыми.

Хотя корни зависят только от вида левой части дифференциального уравнения линейной системы, постоянные интегрирования зависят и от вида правой части. Поэтому вид переходного процесса и быстрота его затухания определяются как левой, так и правой частями. Однако в связи с тем, что устойчивость определяется только фактом наличия или отсутствия затухания переходного процесса, то устойчивость линейной АСУ определяется только корнями характеристического уравнения.

Вещественными корням соответствуют слагаемые, представляющие собой экспоненты:

.

(4.11)

Если , то получаем затухающие экспоненты (рис. 4.4, в).

Положительным корням соответствуют возрастающие экспоненты (рис. 4.4, г).

Комплексные корни всегда попарно–сопряжённые: и . Слагаемые, определяемые этими корнями:

.

(4.12)

Можно показать (с использованием формулы Эйлера), что указанная сумма равна:

(4.13)

где , – новые постоянные.

При получаются затухающие колебания (рис. 4.4, а), а при – расходящиеся колебания (рис. 4.4, б).

При корни будут мнимыми и в системе возникают незатухающие колебания (рис. 4.4, д).

Р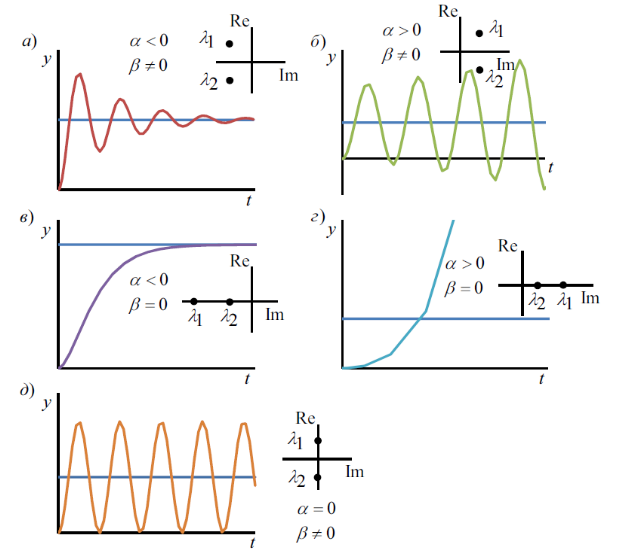исунок 4.4 -  Возможные расположения корней характеристического уравнения на комплексной плоскости и соответствующие переходные характеристики

Время затухания переходного процесса зависит от величины действительной части корня. Чем большее значение действительной части корня, тем быстрее затухает переходной процесс (рис. 4.5).

Рисунок 4.5 - Переходные процессы в звеньях второго порядка

Вычисление корней просто лишь для характеристических уравнений первой и второй степени. Существуют общие выражения для корней уравнений третьей и четвертой степени, но эти выражения громоздки и практически не применяются. Для уравнений более высоких степеней вообще невозможно написать общие выражения для корней через коэффициенты характеристического уравнения.