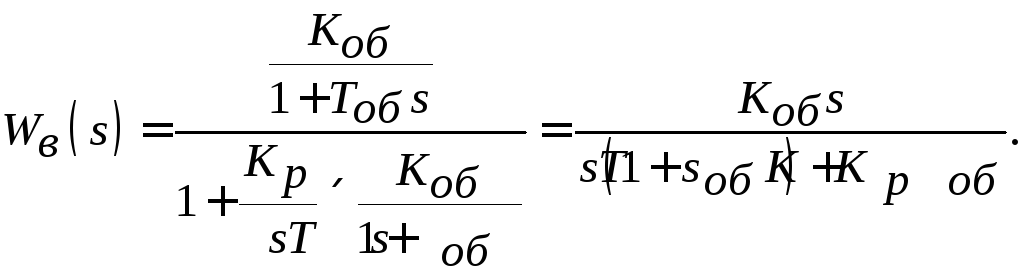- •Печатается в авторской редакции по решению Ученого совета нМетАу, протокол № 10 от 18.12.2009 г.
- •1. Принципы построения, методы анализа и синтеза линейных систем автоматического управления
- •1.1. Основные понятия и определения
- •1.2. Принципы автоматического управления
- •1.2.1. Управление по отклонению
- •1.2.2. Управление по возмущению
- •1.2.3. Комбинированное управление
- •2. Понятие передаточной функции
- •3. Частотные характеристики системы регулирования и ее элементов
- •4. Показатели качества систем автоматического управления
- •4.1. Оценка качества регулирования при стандартных воздействиях
- •4.2. Корневые критерии качества
- •4.3. Частотные оценки качества
- •5. Структурные схемы систем автоматического управления
- •5.1. Элементы структурных схем
- •5.2. Преобразование структурных схем
- •5.2.1. Последовательное соединение звеньев
- •5.2.2. Параллельное соединение звеньев
- •5.2.3. Звено, охваченное отрицательной обратной связью
- •5.2.4. Перенос звеньев
- •6. Типовые звенья систем автоматического управления
- •6.1. Апериодическое звено первого порядка
- •6.1.1. Временные характеристики звена первого порядка
- •6.1.2. Частотные характеристики звена первого порядка
- •6.2. Пропорциональное (усилительное) звено
- •6.3. Интегрирующее звено
- •6.4. Дифференцирующее звено
- •6.5. Звено чистого запаздывания
- •6.6. Звено второго порядка
- •6.6.1. Характеристики звена второго порядка
- •6.6.2. Пример звена второго порядка
- •7. Статический режим работы системы автоматического управления
- •7.1. Статическая ошибка по управлению и возмущению
- •7.2. Выбор типа регулятора
- •8. Устойчивость линейных систем автоматического управления
- •8.1. Понятие устойчивости
- •8.2. Критерий Найквиста
- •8.3. Понятие запаса устойчивости
- •8.4. Анализ устойчивости по лчх
- •9. Расчет регуляторов в системах подчиненного регулирования
- •9.1. Общие сведения
- •9.2. Настройка контура регулирования на модульный оптимум
- •9.3. Особенности настройки контуров регулирования
- •9.3.1. Интегрирующее звено в составе регулятора
- •9.3.2. Интегрирующее звено в составе объекта регулирования
- •9.3.3. Объект регулирования в виде колебательного звена
- •9.3.4. Двукратно интегрирующая система регулирования
- •10. Расчет регуляторов линейных сау по логарифмическим частотным характеристикам
- •10.1. Принципы расчета регуляторов
- •10.2. Расчет и моделирование линейных сау
- •10.2.1. Расчет параметров регулятора и моделирование переходных процессов в контуре управления положением задвижки
- •10.2.2. Расчет параметров регулятора и моделирование переходных процессов в контуре управления высотой воды в баке
- •11. Расчет и моделирование сау с запаздыванием
- •11.1. Общие сведения о ленточном дозаторе
- •11.2. Расчет и моделирование сау ленточного дозатора
- •11.2.1. Расчет параметров регулятора и моделирование переходных процессов в контуре управления положением заслонки
- •11.2.2. Расчет параметров регулятора и моделирование переходных процессов в контуре управления заполнением смесителя
- •11.2.3. Оптимизация параметров в условиях неопределенности
- •12. Разработка замкнутых систем регулирования (метод желаемой лачх)
7. Статический режим работы системы автоматического управления
7.1. Статическая ошибка по управлению и возмущению
Установившийся режим работы системы автоматического управления характеризуется окончанием переходного процесса. В этом случае выходные переменные или являются постоянными величинами (статический режим работы, рис. 7.1), или изменяются с постоянной ошибкой в соответствии с изменением входного сигнала (динамический постоянный процесс, рис. 7.2).
Р исунок
7.1 - Статический режим работы
исунок
7.1 - Статический режим работы
Р исунок
7.2 - Динамический постоянный процесс
исунок
7.2 - Динамический постоянный процесс
Основной характеристикой установившегося режима является статическая ошибка.
При наличии
единичной обратной связи, ошибка
![]() определяется как разность между входным
воздействием
определяется как разность между входным
воздействием![]() и выходной переменной
и выходной переменной![]() в установившемся режиме (рис. 7.1, 7.2).
Различают статическую ошибку по
управлению и по возмущению. Статическая
ошибка по управлению характеризует
ошибку при отработке управляющего
сигнала, а ошибка по возмущению -
отклонение управляемого параметра в
установившемся режиме под действием
возмущения.
в установившемся режиме (рис. 7.1, 7.2).
Различают статическую ошибку по
управлению и по возмущению. Статическая
ошибка по управлению характеризует
ошибку при отработке управляющего
сигнала, а ошибка по возмущению -
отклонение управляемого параметра в
установившемся режиме под действием
возмущения.
Статическую ошибку
можно определить из передаточной функции
системы, используя свойство преобразования
Лапласа. Если в оригинале время
![]() ,
то в выражении изображения
,
то в выражении изображения![]() .
.
Рассмотрим вычисление статической ошибки по управлению для системы, структурная схема которой представлена на рис. 7.3.
Р исунок
7.3 - Структурная схема замкнутой системы
регулирования
исунок
7.3 - Структурная схема замкнутой системы
регулирования
Статическая ошибка
![]() равняется:
равняется:
|
|
(7.1) |
Будем полагать,
что
![]() - звено регулятора, а
- звено регулятора, а![]() - звено объекта управления.
- звено объекта управления.
Для примера возьмем следующие передаточные функции:
|
|
(7.2) |
|
|
(7.3) |
Передаточная функция замкнутой системы регулирования по управлению:
|
|
(7.4) |
Если приравнять
![]() ,
то передаточная функция будет иметь
вид:
,
то передаточная функция будет иметь
вид:
|
|
(7.5) |
Статическая ошибка по управлению (рис. 7.4):
Р исунок
7.4 - График переходных процессов в системе
при отсутствии интегратора в регуляторе
и в объекте регулирования
исунок
7.4 - График переходных процессов в системе
при отсутствии интегратора в регуляторе
и в объекте регулирования

|
|
(7.6) |
Из формулы (7.6) видим, что чем больше коэффициент усиления регулятора, тем меньше ошибка по управлению.
Определим статическую ошибку по возмущению, используя структурную схему на рис. 7.5.
Р исунок
7.5 - Структурная схема замкнутой системы
регулирования с возмущающим воздействием
исунок
7.5 - Структурная схема замкнутой системы
регулирования с возмущающим воздействием![]()
Передаточная функция замкнутой системы регулирования по возмущению:
|
|
(7.7) |
Учитывая то, что
![]() ,
, ,
получим:
,
получим:
|
|
(7.8) |
При
![]() передаточная функция равняется:
передаточная функция равняется:
|
|
(7.9) |
Статическая ошибка по возмущению (рис. 7.4):
|
|
(7.10) |
Из формулы (7.10)
видно, что чем больше коэффициент
усиления регулятора, тем меньше влияет
возмущение на отклонение управляемого
параметра
![]() .
.
Таким образом, при наличии пропорционального регулятора, замкнутая система регулирования (регулятор и объект регулирования не содержат интегратора) имеет статическую ошибку по управлению и по возмущению.
Рассмотрим в качестве регулятора интегрирующее звено:
|
|
(7.11) |
При интегральном регуляторе передаточная функция замкнутого контура по управлению примет вид:
|
|
(7.12) |
При
![]()
![]() .
.
Ошибка по управлению в соответствии с уравнением (7.1) равна нулю (рис. 7.6):
|
|
(7.13) |
Р исунок
7.6 - График переходных процессов в системе
при наличии интегратора в регуляторе.
исунок
7.6 - График переходных процессов в системе
при наличии интегратора в регуляторе.
Эквивалентная передаточная функция по возмущению при интегральном регуляторе имеет вид:
|
|
(7.14) |
При
![]()
![]() .
Таким образом, статическая ошибка по
возмущению, при наличии интегратора в
составе регулятора, равна нулю (рис. 7.6):
.
Таким образом, статическая ошибка по
возмущению, при наличии интегратора в
составе регулятора, равна нулю (рис. 7.6):
|
|
(7.15) |
Таким образом, применение регулятора в виде интегрирующего звена приводит к устранению статической ошибки по управлению и возмущению.

 ,
,
 .
. .
.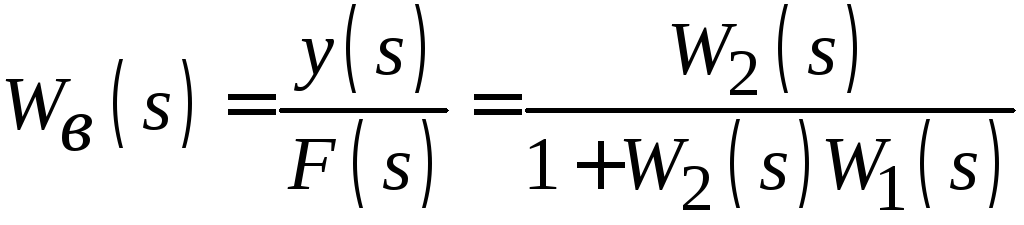 .
.
 .
. .
. .
.