6.6.2. Пример звена второго порядка

Примером звена второго порядка может служить математическое описание двигателя постоянного тока при управлении по цепи якоря и постоянном магнитном потоке (рис. 6.20, 6.21).

Рисунок 6.20 - Механизм подъема груза

Рисунок 6.21 - Силовая часть электроприводу постоянного тока:

а - принципиальная схема, б - схема замещения

Двигатель постоянного тока с независимым возбуждением - наиболее распространенный тип двигателей постоянного тока. При его рассмотрении будем считать, что размагничивающее действие реакции якоря компенсировано, а индуктивность якорной цепи постоянная. Действие вихревых токов, проявляющееся при изменении магнитного потока, учитывается как действие короткозамкнутой обмотки, расположенной на полюсах.

Двигатель постоянного тока (рис. 6.21) имеет обмотку якоря и обмотку возбуждения, которые получают питание от независимых источников постоянного токаи. К якорю двигателя с моментом инерции , который вращается с частотой , приложен электромагнитный момент , под действием которого механическая часть электропривода приводится в движение.

Переходные процессы, которые протекают в двигателе постоянного тока, с учетом механической и электромагнитной инерции, описываются следующими уравнениями.

• уравнение электрического равновесия для цепи якоря;

• уравнение связи электромагнитного момента и тока двигателя;

• уравнение, связи электродвижущей силы (ЕДС) двигателя и частоты вращения;

• уравнение движения электропривода.

.

(6.78)

Система уравнений (6.78) позволяет проанализировать динамические особенности как объекта управления, пользуясь методами теории автоматического управления.

Введем понятие электромагнитной постоянной времени цепи якоря:

,

(6.79)

где - активное сопротивление цепи якоря;- индуктивность цепи якоря.

С учетом формулы (6.79) уравнение электрического уравнения для цепи якоря в операторной форме запишется в виде:

.

(6.80)

По аналогии с электромагнитной постоянной времени введем понятие электромеханической постоянной времени :

,

(6.81)

где - это время, в течение которого привод с моментом инерциипри динамическом моменте, равном моменту короткого замыкания, достигнет скорости идеального холостого хода.

В уравнении (6.81) неизвестны и. Для их определения воспользуемся механической характеристикой двигателя постоянного тока. Рассмотрим точки короткого замыкания и идеального холостого хода.

Режим установившегося короткого замыкания ().

Второе уравнение системы (6.78) и уравнение (6.80) запишутся в виде:

,

(6.82)

где - магнитный поток,- конструктивная постоянная двигателя.

.

(6.83)

Выразим из формулы (6.21) и подставим полученное значение в (6.81):

.

(6.84)

Режим установившегося идеального холостого хода (,,).

ЭДС двигателя в соответствии с третьим уравнением системы (6-73) и уравнением (6.80):

.

(6.85)

Скорость идеального холостого хода:

.

(6.86)

Уравнение (6.81) с учетом (6.84) и (6.86) представим в виде:

.

(6.87)

Преобразуем уравнение движения:

.

(6.88)

Учитывая второе уравнение системы (6.78), получим:

.

(6.89)

Заменим в соответствии с формулой (6.87):

.

(6.90)

На основании выражений (6.80), (6.90) решим систему уравнений (6.78) относительно тока, скорости и ЕДС двигателя:

.

(6.91)

Система (6.91) описывает переходные процессы в двигателе постоянного тока с учетом электромагнитной и механической инерции. Представим эту систему в виде структурной схемы, входами которой является ЭДС преобразователя, питающего якорную цепь и ток нагрузки, выходом - частота вращения двигателя.

Рисунок 6.22 - Структурная схема двигателя постоянного тока без учета контура возбуждения

Передаточная функция двигателя в соответствии с рис. 6.22:

.

(6.92)

Переходные функции двигателя изображены на рис. 6.23.

Рисунок 6.23 - Переходные функции двигателя постоянного тока:

1-; 2-

Вид переходного процесса определяется корням характеристического уравнения (6.30):

.

(6.93)

Корни действительные при или. В этом случае переходной процесс нарастания скорости соответствуетпереходному процессу в двойном апериодическом звене (рис. 6.23, кривая 1):

.

(6.94)

При корни мнимыеи процесс нарастания скорости будет колебательным (рис. 6.23, кривая 2).

В качестве примера, определим переходную характеристику двигателя для структурной схемы (рис. 6.22), при условии питания двигателя от источника бесконечно большой мощности. В этом случае и.

Рассмотрим двигатель постоянного тока со следующими параметрами:

• тип П-82,

• номинальная мощность кВт,

• номинальное напряжение В,

• номинальная скорость ,

• номинальный ток А,

• момент инерции ,

• индуктивность обмотки якоря мГн,

• активное сопротивление обмотки якоря Ом.

Определим параметры, необходимые для моделирования:

 ,

 ,

 ,

.

Подставив полученные значения в структурную схему (рис. 6.22), выполним моделирование. График переходной функции показан на рис. 6.24.

Рисунок 6.24 - Результаты моделирования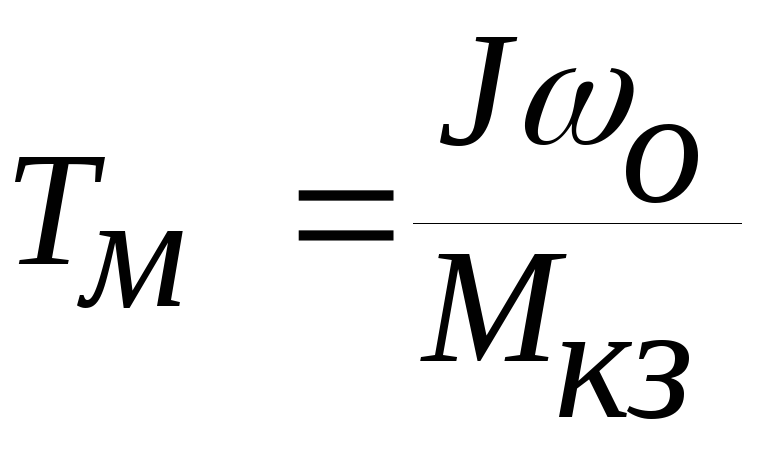