6.1.2. Частотные характеристики звена первого порядка

Комплексный коэффициент усиления для передаточной функции (6.2) определяется как:

.

(6.19)

Для построения графика комплексного коэффициента усиления воспользуемся пакетом Matlab [3]. Зададим передаточную функцию (6.19), введя в командной строке следующую запись . При правильной записи на экране появится передаточная функция указанного звена. После этого набираем команду. График комплексного коэффициента усиления будет изображен в отдельном окне. Чтобы не показывать на графике отрицательные частоты надо в контекстном меню выбрать пункты,.

Для значений , с график АФХ представлен на рис. 6.2.

Рисунок 6.2 - Частотный годограф комплексного коэффициента усиления (диаграмма Найквиста)

АФХ представляет собой полуокружность с радиусом в четвертом квадранте комплексной плоскости и центром в точкена действительной оси.

Для построения логарифмической амплитудно-частотной и логарифмической фазовой частотной характеристик введем команду .

ЛАЧХ в соответствии с уравнением (3.19):

.

(6.20)

ЛФЧХ описывается уравнением (3.15):

.

(6.21)

Для значений , с в пакете Matlab построены ЛАЧХ и ЛФЧХ (рис. 6.3).

Рисунок 6.3 - Графики ЛАЧХ и ЛФЧХ

При частоте получим значение, соответствующее установившемуся режиму:

.

При больших частотах . В этом случае.

Выражение для ЛАЧХ приобретает вид:

.

(6.22)

В этом случае представляет собой прямую, имеющую наклон минус 20 дБ/дек. Действительно, при увеличении на декаду, т.е. в десять раз,

.

Таким образом, величина уменьшилась на, т.е. на 20 дБ.

При значениеизменяется отдо. В точкефазовый сдвиг приобретает значение.

Для получения АЧХ и ФЧХ надо из контекстного меню выбрать пункт . Открыть вкладку(рис. 6.4). Свойства осей следует перевести из логарифмического масштаба в обычный масштаб, как показано на рис. 6.4, а, б.

а – логарифмический масштаб осей	б – обычный масштаб осей

Рисунок 6.4 - Вкладка

После изменения масштаба осей на графиках будут изображены АЧХ и ФЧХ для значений , (рис. 6.5).

Р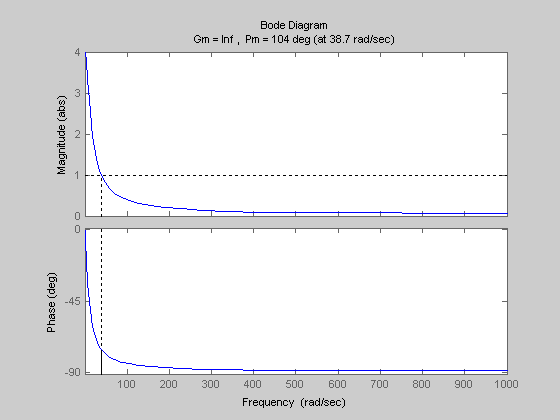исунок 6.5 - Графики АЧХ и ФЧХ

6.2. Пропорциональное (усилительное) звено

Выходная величина этого звена пропорциональная входной величине . Уравнение звена:

,

(6.23)

где - коэффициент усиления звена.

Передаточная функция звена

.

(6.24)

Примером такого звена является усилитель постоянного тока (рис. 6.7).

Рисунок 6.6 - Усилитель на базе операционного усилителя

Коэффициент усиления равняется:

.

(6.25)

Предполагается, что передача сигнала от входа звена к выходу звена осуществляется мгновенно (безинерционно). Поэтому пропорциональные звенья называют безинерционными.

Если, на вход пропорционального звена подать единичный ступенчатый сигнал , то выходной сигнал будет изменяться в соответствии с выражением:

.

(6.26)

Переходная характеристика звена изображена на рис. 6.7.

Рисунок 6.7 - График переходной характеристики интегрирующего звена

Частотные функции звена:

.	(6.28)
.	(6.29)
.	(6.30)
.	(6.31)
.	(6.32)
.	(6.33)

Графики ЛАЧХ и ЛФЧХ для пропорционального звена при изменении от 0 до 10иприведены на рис. 6.8.

Рисунок 6.8 - ЛАЧХ и ЛФЧХ пропорционального звена

Как и следовало ожидать, запаздывание по фазе выходного сигнала отсутствует.
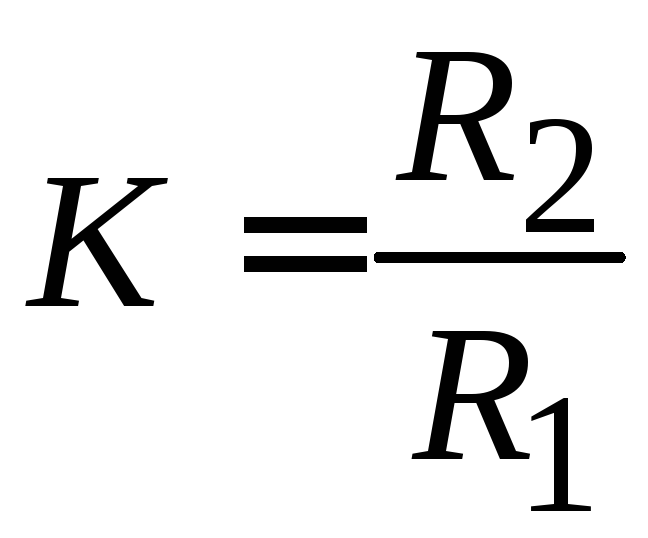