5.2.4. Перенос звеньев

При преобразовании структурных схем иногда необходимо переносить звенья через узел разветвления, как в направлении передачи сигнала, так и в противоположном направлении.

Рассмотрим перенесение звена через узел разветвления по направлению передачи сигнала (рис. 5.9).

Рисунок 5.9 - Перенос звена через узел разветвления по направлению передачи сигнала

При такой операции в цепи добавляют фиктивные звенья с передаточной функцией перенесенного звена.

При перенесении звена через узел разветвления в направлении обратном передаче сигнала (рис. 5.10) в цепь добавляют фиктивное звено с передаточной функцией обратной передаточной функции звена, через которое выполнен перенос.

Рисунок 5.10 - Перенос звена через узел разветвления в направлении обратном передаче сигнала

6. Типовые звенья систем автоматического управления

Объекты в теории автоматического управления описываются передаточными функциями, содержащими полиномы от произвольного порядка в числителе и знаменателе. Но, если передаточная функция объекта содержит только простой множитель в числителе, либо в знаменателе, то объект называется типовым динамическим звеном (типовым звеном).

Из курса алгебры известно, что полином любого порядка можно разложить на простые множители. То есть любую САУ можно представить в виде последовательного соединения типовых звеньев. С другой стороны, реальные звенья САУ могут иметь самую разнообразную физическую основу (электронные, механические, гидравлические, электромеханические и т.п.) и конструктивное выполнение, но иметь одинаковые передаточные функции и являться одинаковыми типовыми звеньями. Поэтому знание характеристик звеньев столь же необходимо для расчетов САУ, как знание таблицы умножения в арифметике.

Все линейные типовые звенья разделяют на три основных группы:

• позиционные звенья,

• интегрирующие звенья,

• дифференцирующие звенья.

Позиционные звенья: апериодическое, пропорциональное, колебательное, консервативное и чистого запаздывания - характеризуется тем, что в каждом из них, кроме консервативного, при подаче на вход постоянной величины с течением времени устанавливается постоянное значение выходной величины.

В интегрирующих звеньях при постоянном входном воздействии выходная величина неограниченно растет.

Дифференцирующие звенья характеризуются тем, что реагируют только на изменение входной величины.

Рассмотрим типовые звенья и их характеристики.

6.1. Апериодическое звено первого порядка

6.1.1. Временные характеристики звена первого порядка

Динамические процессы в звеньях первого порядка описываются дифференциальными уравнениями первого порядка:

.

(6.1)

Передаточная функция апериодического звена первого порядка (6.1) после преобразования Лапласа имеет вид:

.

(6.2)

Решение уравнения (6.1) можно записать в виде [4]:

,

(6.3)

где - установившаяся (вынужденная) составляющая;- переходная составляющая изменения выходной координаты во времени.

Установившаяся составляющая определяется входным сигналом, а переходная - свойствами самой системы. Будем искать общее решение уравнения (6.1) в следующем виде:

,

(6.4)

где и- пока неопределенные коэффициенты.

Подставим выражение (6.4) в (6.1). Приравняв правую часть уравнения к нулю, получим:

,

(6.5)

или

.

(6.6)

Очевидно, что уравнение выполняется при любых значениях , если.

Выражение называется характеристическим уравнением исходного дифференциального уравнения. Если сравнить выражениесо знаменателем передаточной функции (6.2), то видно, что они имеют один и тот же вид. Если в знаменателе передаточной функции подставитьвзамени приравнять это выражение к нулю, то получим характеристическое уравнение:

.

(6.7)

Таким образом, переходная составляющая дифференциального уравнения (6.1) имеет вид:

.

(6.8)

Решим дифференциальное уравнение (6.1) при входном сигнале в виде единичного ступенчатого скачка:

,	(6.9)
.	(6.10)

Постоянное значение определяется для значений времени.

Переходная составляющая стремится к нулю, так как

.

(6.11)

В этом случае, согласно уравнению (6.3), установившееся значение и равняется.

Запишем выражение (6.3) в виде:

.

(6.12)

Найдем значение коэффициента при нулевых начальных условиях,,. Тогда уравнение (6.12) имеет вид:

.

(6.13)

Отсюда определим :

.

(6.14)

Окончательно уравнение (6.3) запишется:

.

(6.15)

На рис. 6.1 показанный график переходной характеристики для значений ,.

Рисунок 6.1 - Переходная характеристика апериодического звена первого порядка

Рассмотрим характерные точки на переходной характеристике, которые определяют показатели качества.

Время регулирования определяется моментом времени, когда значение переходной характеристики попадает в «коридор»и больше не выходит за его пределы. Значениедостигается за время. Действительно:

.

(6.16)

Таким образом, продолжительность переходного процесса равняется:

.

(6.17)

Коэффициент называется постоянной времени.

Если на графике переходного процесса из точки опустить перпендикуляр на ось времени, то полученное значение будет численно равно постоянной времени. Действительно:

.

(6.18)

Переходная характеристика апериодического звена (рис. 6.1) не имеет колебаний, и его параметры определяются коэффициентом усиления (передачи) и постоянной времени.
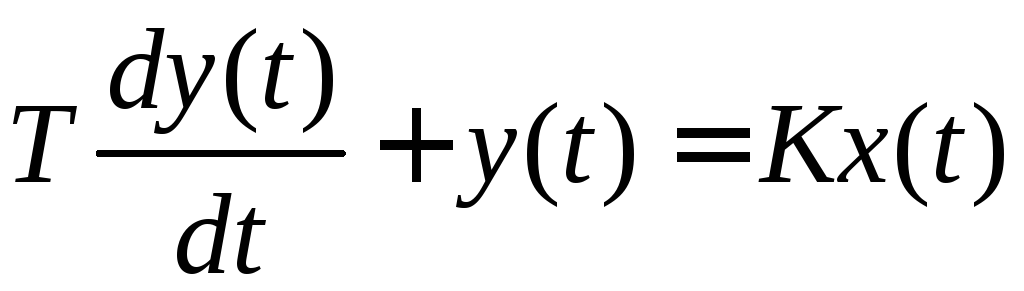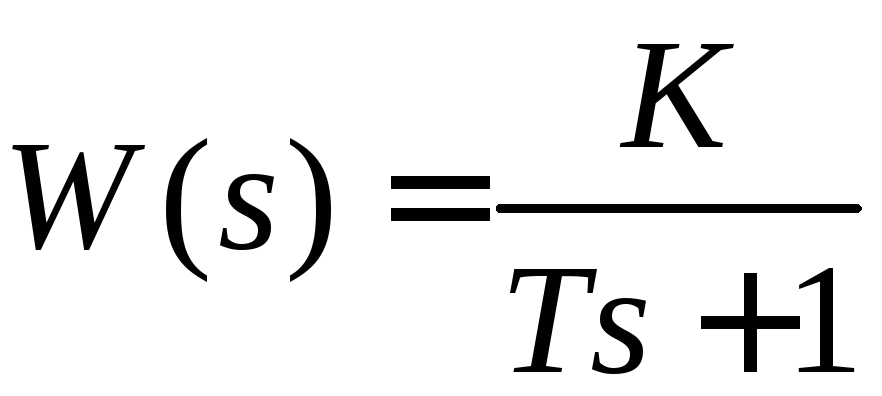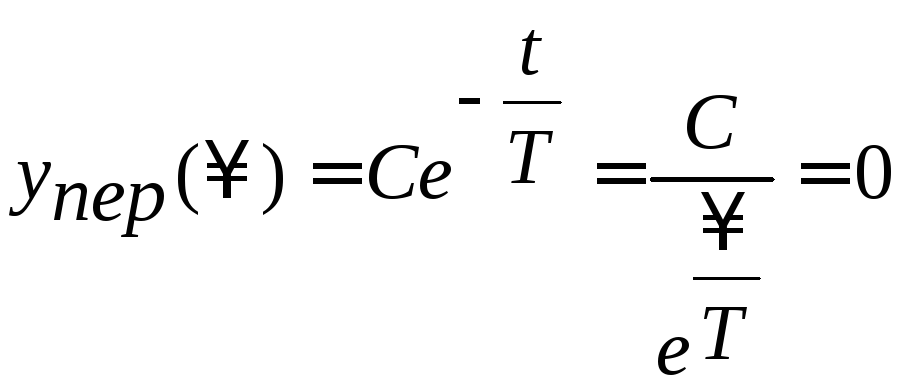