Контрольні запитання
Етапи рішення нелінійних рівнянь. Відділення коренів.
Уточнення коренів методом ділення відрізка наполовину.
Блок-схема методу ділення відрізка наполовину.
Уточнення коренів методом Ньютона (дотичних). Блок-схема методу.
Уточнення коренів методом хорд (січних).
Блок-схема методу хорд (січних).
Уточнення коренів методом ітерацій (методом послідовних приближень).
Скласти блок-схему методу послідовних приближень.
Структура програми на мові програмування Turbo C. Основні поняття.
Правила оформлення допоміжної функції в структурі програми.
Тема iІ. Чисельне рішення систем лінійних алгебраїчних рівнянь Лабораторна робота №5. Рішення систем лінійних алгебраїчних рівнянь методом Гауса
1. Мета роботи
Освоєння методу рішення систем лінійних алгебраїчних рівнянь. Вивчення та використання прикладних програм із бібліотеки програм ХТФ ОНПУ.
2. Теоретичні відомості
Нехай дана система nлінійних алгебраїчних рівнянь зnневідомими:
a11x1 + a12x2 +.....+ a1nxn = b1
a21x1 + a22x2 +.....+ a2nxn = b2
...................................................
an1x1 + an2x2 +.....+ annxn = bn
(2.1)
чи у матричному вигляді
A X = В, (2.2)
де
А = (aij) =
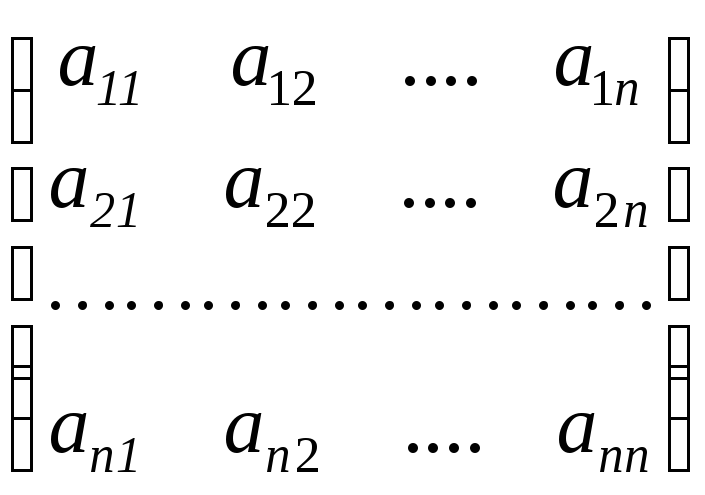–матриця коефіцієнтів,
,
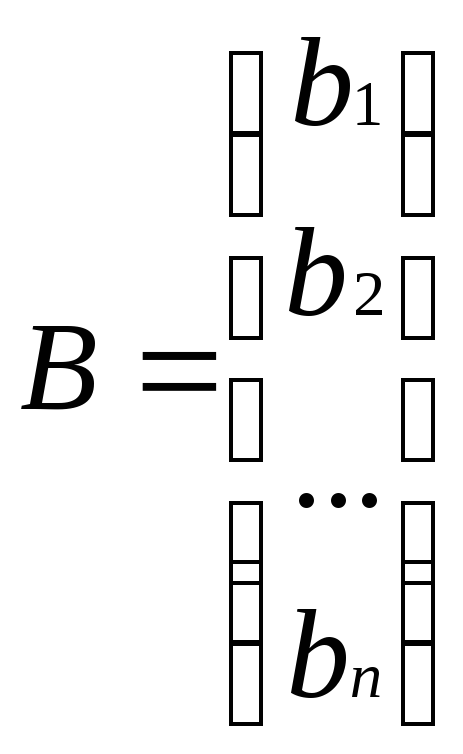– стовпець вільних членів та стовпець
невідомих відповідно.
Коефіцієнти системи (2.1) характеризуються двома індексами. Перший індекс – івизначає номер строки, другий –j– номер стовпця.
Рішення системи (2.1) складається зі знаходження таких значень невідомих, при підстановці яких у висхідну систему кожне з рівнянь перетворюється у тотожність.
Якщо матриця A неособлива , то
det A =
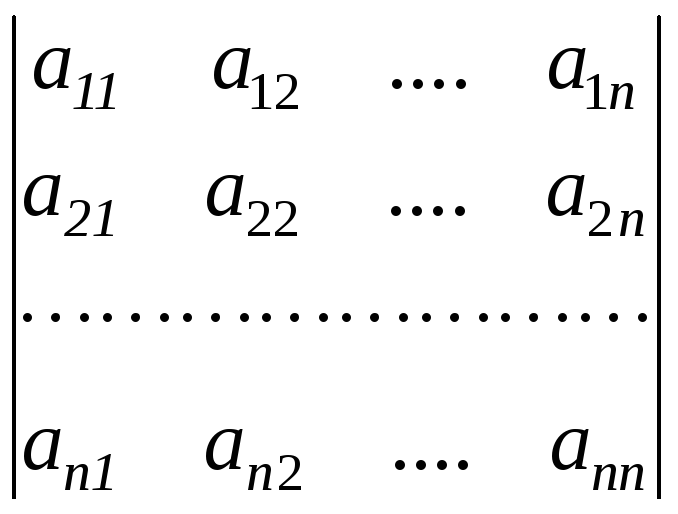
0
та система (2.1) має одиничне рішення.
Способи рішення систем лінійних рівнянь (СЛР) у основному діляться на дві групи .
1. Точні методи, які являють собою кінцеві алгоритми для обчислювання коренів системи (правило Крамера, метод Гауса, метод головних елементів, метод квадратних коренів та інші).
2. Ітераційні методи, які дозволяють одержувати корні системи із заданою точністю шляхом збіжних безкінечнихпроцесів (метод ітерацій, метод Зейделя, метод релаксації).
2.1. Метод Крамера
Значення невідомих xi(i =1,2,...,n) можуть бути одержані по формулам Крамера:
xi=
,
де матриця Аiвизначається з матриціАзаміноюi-того стовпця стовпцем вільних членів.
Такий спосіб рішення лінійних систем із n невідомими приводить до обчислюванняn+1детермінанту порядкуn, що представляє собою дуже складну операцію приякомусь великому числіn.
2.2. Метод Гауса
Найбільш розповсюдженим методом рішення систем алгебраїчних рівнянь являється метод Гауса, в основі якого лежить ідея послідовного виключення невідомих. Існують різні обчислюванні схеми, що реалізують цей метод. Розглянемо одну з них – схему єдиного ділення.
Хай задана система лінійних рівнянь n-го порядку, детермінант якої не є нуль. Припустимо, що матриця коефіцієнтів не має нульових діагональних елементів. Якщо такі маються, то відповідною перестановкою рядка їх завжди можна зробити ненульовими.
Метод Гауса полягає у наступному:
1. З усіх рівнянь, крім першого, виключаються члени, які містять x1. Для цього з другого, третього,.....,n-го рівнянь системи почленно, включаючи праві частини, віднімаються перше рівняння, поділене наа11та помножене відповідно наа21,а22,а23,....., аn1. У результаті цієї операції порядок усіх рівнянь, за виключенням першого, понижується на одиницю.
2. Знову отримане друге рівняння ділиться на а22–(а12/а11)а21та аналогічним способом, починаючи з третього рівняння, виключаються усі елементи, які містятьх2.
3. Повторюємо цю процедуру n–1 разів, тобто кожен раз, виключаючи невідомі з нижче розташованих рівнянь, можна отримати в результаті ступінчату трикутникову систему рівнянь, еквівалентну першій, останнє рівняння якої має тільки одну невідому.
4. Рішення ступінчатої системи рівнянь здійснюється шляхом послідовного обчислювання невідомих, починаючи з останнього рівняння.
ПРИКЛАД: Для визначення вмісту компонентів початкової суміші необхідно вирішити наступну систему рівнянь:
-
2,0 x1 + 1,0 x2 – 0,1 x3 = 3,7
0,4 x1 + 0,5 x2 – 4,0 x3 = 13,4
0,3 x1 – 1,0 x2 + 1,0 x3 = 1,3
Для вирішення системи використовуємо метод Гауса. З другого та третього рівняння виключимо члени, які містять х1. Для цього спочатку поділимо перше рівняння наа11 = 2,0. Отримаємо:
х1 + 0,5 x2 – 0,05 – x3 = 1,85
Потім, помножимо отримане рівняння на а21таа31, віднімемо з другого та третього рівнянь відповідно. Таким чином отримаємо систему з двома невідомими:
0,3 x2 + 4,02 x3 = 12,66
––1,15 x2 + 1,015 x3 = 0,745
Поділив перше рівняння отриманої системи на а22та помножив його наа32, вирахуємо з другого рівняння цієї системи.
16,425 x3 = 49,275
Таким чином, еквівалентна система має вигляд:
x1 + 0,5 x2 – 0,05 x3 = 1,85
x2 + 13,4 x3 = 42,2
16,425 x3 = 49,275
З отриманої еквівалентної системи послідовно знайдемо:
x3 = 3,0
x2 = 42,2 – 13,4 3,0 = 2,0
x1 = 1,85 – 0,5 2,0 + 0,05 0,3 = 1,0
Процес побудування еквівалентної трикутної системи називається прямим ходом, а процес знаходження значень невідомих – зворотнім ходом.
2.3. Блок-схема програми для рішення систем лінійних рівнянь методом Гауса
Блок-схему програми можна поділити умовно на три частини. Перша – реалізує алгоритм виключення невідомих; друга – зворотну підстановку; третя – визначає найбільший коефіцієнт при хта переставляє рівняння при необхідності.
У блок-схемі усі множники позначаютьсяодним та тим же символомm. Якщо обчислювання у програмі вірно організовані, то кожний етап обчислювань не потребує більш одного множника.
При аналізі блок – схеми треба чітко представити зміст індексів i, j, k:
k– визначає номер того рівняння, яке віднімається з тих,що залишилися,а також номер того невідомого, яке виключається з тих, котрі залишилися,n–kрівнянь;
i– означає номер рівняння, з якого у цю мить виключаються невідомі;
j– означає номер стовпця.
Блок-схема послідовного виключення невідомих представлена на рис. 2.1.
Зворотна підстановка для находження значення невідомих задається наступними формулами:
x n =
;
xn–1 =
;
......................................
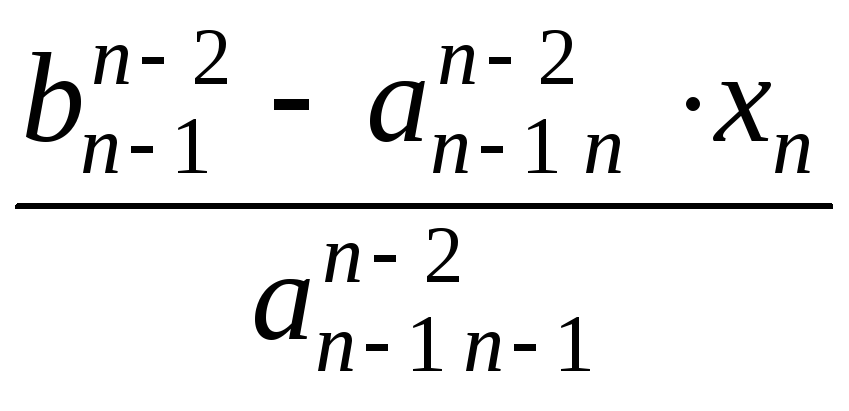xj =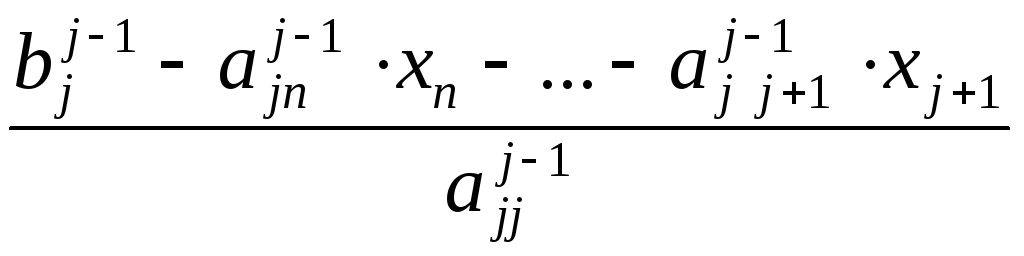
для j = n–2, n–3, ..., 1.
Блок-схема зворотного ходу представлена на рис. 2.2. Помітимо, що у блок–схемі (рис. 2.1) усі індекси у процесі обчислювання збільшуються, а у блок-схемі (рис. 2.2) один з індексів, а саме i, зменшується.
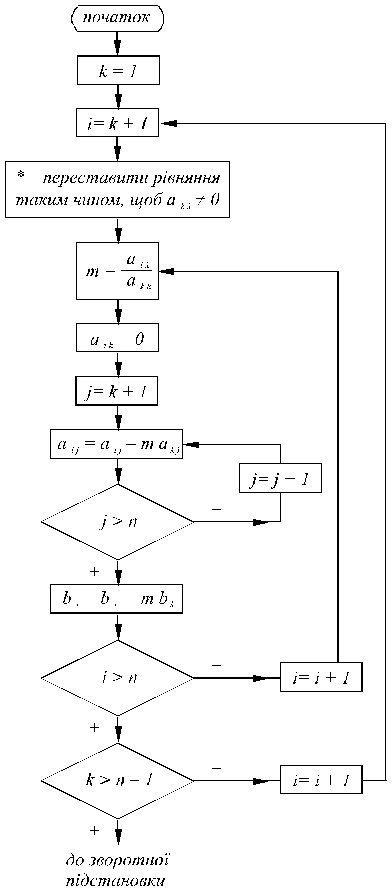
Рис. 2.1. Блок-схема послідовного виключення невідомих
Рис. 2.2. Блок-схема зворотної підстановки
Розглянемо третю блок-схему перестановки рівнянь, яка входить у блок–схему (2.1). Завдання знаходження найбільшого коефіцієнта при xkта перестановці рівнянь при необхідності пов'язана зі зменшенням помилкиокруглення, яка виникає при обчислюванні з числами з плаваючою комою. По-перше, перестановка може бути потрібна, для того щобakk 0(щоб ухилитися від ділення на 0). А також, використовуючи перестановку, можливо зменшити помилку округлення.
Спочатку розглянемо числовий приклад. Розв'яжемо систему:
3,241102 x1+1,600102 x2 = 1,632102
1,020104 x1+1,540103 x2 = 1,174104
Точне рішення цієї системи наступне:
x1=1,000100 ; x2=1,000100 .
Вирішимо ці рівняння методом виключення у тому порядку, у якому вони записані, використовуючи при обчисленні числа з 4 значущими цифрами у мантисі. Так як а11 0, то можна рішити по відомій схемі.
Перший та єдиний множник:
m = 1,020104 / 3,241100 = 3,147103
Перетворене друге рішення має вигляд:
5,73010–1 x1 – 5,020105 x2 = –5,019105
Коефіцієнт при х1повинен був бути 0, але помилка округлення не дозволяє отримати точний результат. Так як цей коефіцієнт не приймає участі у подальшому обчислюванні, то приймаємо його за 0 та утворюємо зворотну підстановку:
x2 = –5,019105 / –5,020105 = 9,99810–1
З першого рівняння одержуємо:
x1 = 9,87310–1.
Зараз підставимо рівняння так, щоб максимальний по модулю елемент попав на головну діагональ:
1,020104 x1 + 1,540103 x2 = 1,174104
3,241100 x1 + 1,600102 x2 = 1,632102
Зараз множник
m = 3,241100 / 1,020104 = 3,17710–4
Перетворене друге рівняння:
0,000 x1 + 1,595102 x2 = 1,595102
Звідки x2 = 1,000100 ; x1=1,000100.
У цьому прикладі коефіцієнти дуже відрізняються по величині, але частіше ця різниця не так велика. Однак при рішенні великої системи рівнянь помилки округлення можуть накопичуватисята відповіді можуть не містить ні одної вірної цифри. Тому при рішенні СЛР на ЕОМ методом виключення повинно передбачити можливість перестановки рівнянь.
Отже, завдання зводиться до перестановки n–k+1останніх рівнянь так, щоб найбільший по модулю коефіцієнт приxkпопав на головну діагональ. Описаний спосіб рішення СЛР називають методом головного елементу.
При розгляданні блок–схеми необхідно пам'ятати, що при переході до даного етапу індекс k, що обчислюється, має деяке визначене значення, аi=k+1 (дивись рис. 2.3).
1. Спочатку у програму вводиться допоміжний індекс l, якому надається значенняk.
2. Перше порівняння робиться між елементом акl, який лежить на головній діагоналі, та наступним за нимaik. Якщо|aik|>|alk|, то індексуlнадають значенняiта подальше порівняння виконується з другим елементом.
Рис. 2.3. Блок–схема перестановки рівнянь
Тому індекс lявляється номером елементу, який з'явився при порівнянні більше двох елементів по модулю. Індексіпробігає за ходом програми значення відk+1доnвключно, та у кінці цього циклу індексlвизначає номер найбільшого по модулю елементу уk-ому стовпці. При перестановці рівняння цей коефіцієнт повинен попасти на головну діагональ.
Може статися так, що значення аік вже являється найбільшим по модулю елементом. Тому така можливість відразу перевіряється і в такому випадку перестановка не проводиться.
Фактично процес полягає у перестановці коефіцієнтів, один з яких утримується у рівнянні k, а другий – у рівнянніl, яким би не було значенняl.
Перестановку можна провести за допомогою трьохступеневого процесу. Цю перестановку необхідно виробити для усіх пар коефіцієнтів двох рівнянь.
Перед поверненням до основного процесу обчислювань необхідно відновити первісне значення індексу і, який було використано при порівнянні. Так як перед початком процесу індексімав значенняk+1, то наприкінці блоку йому надається попереднє значенняi = k+1.