2.4 Операторные передаточные функции

35

где р01, р02,…., р0m – нули операторной передаточной функции H ( p) . При

подстановке нулей в выражение (2.38) операторная передаточная функция H ( p) обращается в ноль; р1, р2,…., рn – полюсы операторной передаточной

функции H ( p) . При подстановке полюсов в выражение (2.38) значение H ( p)

стремится к бесконечности.

В выражении (2.38) коэффициент

H = bm . an

Степень полинома числителя „m” и знаменателя „n” зависят от числа реактивных элементов цепи.

Заменив в (2.33...2.35) оператор „р” на „jω”, получим комплексную передаточную функцию цепи H ( jω) . Таким образом, заменяя „jω” на „р”,

можно автоматически получить законы теории электрических цепей и методы расчета в операторной форме.

Свойства операторных передаточных функций:

1Операторная передаточная функция является дробно-рациональной функцией с вещественными коэффициентами (2.37). Вещественность коэффициентов объясняется тем, что они определяются элементами цепи.

2Степень полинома числителя не превышает степень полинома

≤n .

3 Нули и полюсы операторной передаточной функции H ( p) являются либо вещественными числами, либо комплексно-сопряженными.

где p = −σ± jω.

Если полюсы операторной передаточной функции находятся в правой

полуплоскости рисунка 2.8, то такая цепь является неустойчивой: e pt , где p = +σ± jω.

При чисто мнимых полюсах (полюсы расположены на оси мнимых чисел), состояние цепи называют условно устойчивой: e pt , где p = ± jω.

Тогда согласно принципу суперпозиции (наложения) и выражению (2.46) получим связь между переходной функцией цепи h(t) и комплексной передаточной функцией H(jω):

Используя связь между единичной ступенчатой функцией 1(t) и функцией Дирака δ(t) можно показать, что:

Согласно принципу суперпозиции можно доказать связь между импульсной функцией g(t) и комплексной передаточной функцией H(jω):

Выражение (2.49) представляет собой обратное преобразование Фурье, где H(jω) является спектральной плотностью импульсной характеристики цепи.

На основании прямого преобразования Фурье:

−∞

Выражения (2.47)…(2.50) показывают связи между временными и частотными функциями цепи.

2.6 Анализ цепей с обратной связью. Критерии устойчивости

Анализ цепей с обратной связью

Рассматриваемые ранее методы анализа электрических цепей (суперпозиции, узловых напряжений, эквивалентного генератора и др.) хорошо “работают” в цепях, представленных в виде соединений двухполюсников. Для цепей, составленных из четырехполюсников, удобно пользоваться матричными методами анализа.

В телекоммуникационных системах прохождение сигналов часто происходит таким образом, что часть сигнала с выхода какого либо блока подается обратно на вход. Эта операция производится с целью изменения свойств устройств передачи и улучшения качества передаваемых сигналов. Цепи с такими свойствами называются цепями или системами с обратной связью. Теория этих цепей весьма обширна и разрабатывается давно [4]. Наша задача дать краткое представление этой теории. Чтобы проанализировать

41

активных фильтров и т.д. Положительная обратная связь, в основном, используется в схемах автогенераторов.

Критерии устойчивости

Для определения электрической устойчивости цепей существуют методы, с помощью которых можно определить где располагаются корни характеристического уравнения системы с обратной связью N(p) = 0.

Критерий Рауса-Гурвица (алгебраический) позволяет, не решая характеристическое уравнение по его виду и величине коэффициентов при членах с разной степенью р сделать вывод о наличии мнимых или комплексносопряженных корней с положительными вещественными составляющими. Иными словами найти корни, лежащие на мнимой оси или в правой

(1). Для того чтобы корни этого уравнения располагались в левой полуплоскости (условие устойчивости) все коэффициенты an,…а0 должны быть не нулевыми и иметь одинаковый алгебраический знак. Коэффициенты характеристического уравнения выписываются в такой последовательности:

где коэффициенты bi, ci, di образуются по правилу:

d1 = c1b2 c−b1c3 ........

1

Если знак членов первой колонки (2.52) не изменяется, все корни уравнения (2.51) лежат в левой полуплоскости и цепь устойчива. Критерий утверждает, что передаточная функция цепи имеет столько полюсов в правой полуплоскости, сколько раз изменяется знак в ряде an, an-1, b, c, d,…

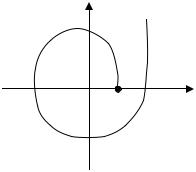
Критерий Михайлова (частотный). Суть метода заключается в том, что на основе характеристического уравнения цепи N(р) = 0 строится частотный годограф. Цепь будет устойчива, если годограф при изменении частоты ω от 0

42

до ∞ последовательно пройдет n квадрантов против часовой стрелки, начиная с положительной вещественной оси, где n – степень характеристического уравнения. На рис. 2.13 приведен годограф Михайлова для устойчивой цепи пятого порядка.

ный характер характеристики функции N(р) нарушится и ход годографа Михайлова изменится. Для устойчивой цепи частоты, при которых годограф пересекает вещественную и мнимую оси рис. 2.13, должны удовлетворять неравенству:

Критерий устойчивости Найквиста. В литературе по автоматическому управлению критерий Найквиста называют амплитудно-фазовым критерием. Данный критерий может быть применен только тогда, когда предварительно проверено отсутствие полюсов в правой полуплоскости возвратной разности N( p) =1 − K( p)T ( p) знаменателя передаточной функции системы.

Критерий устойчивости Найквиста служит для проверки устойчивости системы (предложен в 1930 г.) Он позволил разработать различные способы анализа и синтеза систем. Хорошо работает в тех случаях, когда частотные характеристики системы заданы графически. Критерий основан на теореме функции комплексного переменного о комформном преобразовании замкнутых кривых из р-плоскости в плоскость функции N(р).

Строгий вывод критерия Найквиста можно выполнить с помощью теории вычетов.

Критерий корневого годографа. Корневым годографом называют траекторию перемещения корней характеристического уравнения системы с обратной связью N ( p) =1− K ( p)T ( p) в комплексной плоскости при

изменении коэффициента усиления К(р) от 0 до ∞. Для устойчивой системы траектория корней лежит в левой полуплоскости при всех заданных значениях. Передаточные функции усилителя К(р) и цепи обратной связи Т(р) можно записать в виде: