Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесская национальная академия связи им. А.С. Попова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Модуль 3.pdf

Скачиваний:

133

Добавлен:

10.02.2016

Размер:

1.56 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 135 6 7 8 9 10 11 12 13 > Следующая >>>

Если воздействие f1 (t) непериодический сигнал

и имеет разрывы первого рода, то в интегралах Дюамеля (1.29) и в других формах записи добавляются слагаемые, отображающие действия разрывов. Например, пусть сигнал f1 (t) при t = t1 имеет разрыв

первого рода. В этом случае отклик записывают для отдельных интервалов непрерывности воздействия f1 (t) :

1) при 0 ≤t <t1 отклик цепи имеет вид:

f1(t)

f1(t1)

	f1(0)	t
	0	t
	0	t1

Рисунок 1.28 – Сигнал с разрывом

	t1	′
f2 (t) =	f1(0) h(t) + ∫		− x)dx ;	(1.30)
		f1(x) h(t1

x=0

2) при t ≥ t1 отклик цепи имеет вид:

	t1	′
f2 (t) =	f1(0) h(t) + ∫		− x)dx − f1(t1) h(t −t1) ; (1.31)
		f1(x) h(t1

x=0

Вправой части выражения (1.31) третье слагаемое f1 (t1 ) h(t −t1 ) имеет

отрицательный знак, т.к. скачок (разрыв первого рода) воздействия f1 (t) при t = t1 направлен вниз. При скачках воздействия, направленных вверх, подобные слагаемые должны быть положительными.

1.3.3 Дифференцирующие и интегрирующие цепи

Дифференцирующие цепи (ДЦ) и интегрирующие цепи (ИЦ) широко применяются в радиотехнических устройствах, в импульсной технике и системах телекоммуникации.

Цепь называют дифференцирующей, если отклик u2(t) пропорционален производной от приложенного к цепи воздействия u1(t): u2 (t) α1 u1′(t) .

Цепь называют интегрирующей, если отклик u2(t) пропорционален интегралу от приложенного к цепи воздействия u1(t): u2 (t) α2 ∫u1 (t)dt .

Коэффициенты α1 и α2 зависят от
элементов цепей.		iC(t)	С
Проанализируем простейшую ДЦ,
рис. 1.30.		u1(t)	R	u2(t)
Дифференцирование выполняется		u1(t)	R	u2(t)
Дифференцирование выполняется
при условии:
1		Рисунок 1.30 – Дифференцирующая
ωC >> R .			цепь
Тогда напряжение	на емкости

											24
u		(t) ≈ u (t)	, а ток в емкости	i =C	duC (t)		. Напряжение u			(t) найдем по закону
			, а ток в емкости	i =C			. Напряжение u			(t) найдем по закону
	C			C				2
	C	1			dt
Ома					dt
Ома
			u2 (t) = iC (t)R RC			duC (t)		RC	du1 (t)	.	(1.32)
			u2 (t) = iC (t)R RC					RC	dt	.	(1.32)
							dt		dt

Согласно (1.32) отклик цепи u2(t) действительно пропорционален производной от приложенного воздействия u1(t) с коэффициентом пропорциональности α1, равным постоянной времени рассматриваемой ДЦ:

Проанализируем простейшую

iC(t)	R
u1 (t)	C	u2(t)

Рисунок 1. 31 – Интегрирующая цепь

α1 = RC .

интегрирующую цепь (рис. 1.31). Интегрирование выполняется при условии:

R >>	1	. Тогда ток в цепи iC (t)	u1 (t)	, а
	ωC		R

напряжение на емкости определяется по формуле:

uC (t) =u2 (t) = C1 ∫iC (t)dt RC1 ∫u1 (t)dt . (1.33)

Согласно (1.33) отклик цепи u2(t) действительно пропорционален интегралу от приложенного воздействия u1(t) с коэффициентом пропорциональности α2 , равным величине, обратной

постоянной времени рассматриваемой ИЦ:

α2 = RC1 .

Таким образом, чем меньше постоянная времени ДЦ, тем качественнее выполняется дифференцирование входного сигнала (воздействия). Чем больше постоянная времени ИЦ, тем качественнее выполняется интегрирование входного сигнала.

Кроме рассмотренных цепей, операции дифференцирования и интегрирования могут выполнять также цепи, содержащие индуктивность, рис. 1.32.

R			L
R
u1(t)	L	u2(t) u1(t)	R	u2(t)
а)			б)

Рисунок 1.32 – Дифференцирующая(а) интегрирующая (б) цепи

На рис. 1.32, а, изображена ДЦ с коэффициентом пропорциональности α1, равным постоянной времени цепи:

α1 = RL .

На рис. 1.32, б, изображена ИЦ с коэффициентом пропорциональности

α2 , равным величине, обратной постоянной времени цепи:

α2 = RL .

2 ОПЕРАТОРНЫЕ МЕТОДЫ АНАЛИЗА ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Анализ электрических цепей классическим методом сводится к решению дифференциальных уравнений. Основные трудности такого анализа заключаются в определении постоянных интегрирования. По мере усложнения цепей и возрастания порядка дифференциальных уравнений трудности, связанные с определением постоянных интегрирования, увеличиваются.

Значительно большими возможностями обладает операторный метод анализа переходных процессов. Операторный метод так же, как и метод комплексных амплитуд относится к символическим методам. Сущность операторного метода заключается в том, что решение задачи анализа цепи переносится из области функций действительного переменного t в область функций комплексного переменного p = σ + jω. В результате система интегродифференциальных уравнений переменной t заменяется системой алгебраических уравнений комплексной переменной p. Далее по полученному результату решения алгебраических уравнений выполняется обратный переход в область функций действительного переменного. Базируется операторный метод на преобразованиях Лапласа.

2.1 Прямое преобразование Лапласа и его свойства

Пусть некоторая функция времени f(t) (ток или напряжение) удовлетворяет следующим условиям:

1)f(t) = 0 при t < 0;

2)функция f(t) возрастает не быстрее некоторой показательной

функции M eσ0t , т. е.

f (t) < M eσ0t ,

где М > 0, σ0 ≥ 0 (положительные постоянные числа). Принято говорить, что функция имеет ограниченный рост, если показатель роста σ0 конечен.

Из курса математического анализа известно, что если f(t) имеет ограниченный рост, то интеграл

jω

σ0

Рисунок2.1 – Комплексная плоскость

	26
∞
F( p) = ∫ f (t)e−pt dt	(2.1)
0

сходится абсолютно и является аналитической функцией комплексного переменного p = σ + jω в полуплоскости Re [p] = σ > σ0 (рис. 2.1).

Интегральное уравнение (2.1) является

прямым преобразованием Лапласа; функция f(t) называется оригиналом, а F(p)

изображением по Лапласу.

В литературе используются следующие виды символов, связывающих оригинал с его изображением:

L[ f (t)] = F( p), f (t) F( p), f (t) .=.F( p).

При анализе переходных процессов часто полагают, что в некоторый момент времени, принятый за начало отсчета (t = 0), в электрическую цепь включается источник постоянного, гармонического или иной формы напряжения (тока). Обозначим это напряжение (ток) функцией f(t). Для всех значений t < 0 функция f(t) принимается равной нулю. Простейшими оригиналами являются единичная и показательная функции.

Единичная ступенчатая функция [f(t)=1(t)].

1(t)

Графическое

представление

единичной

ступенчатой функции приведено на рис. 2.2.

Аналитическое

представление

единичной

ступенчатой функции

t ≥ 0,

1 при

f (t) =

Единичная

0 при t < 0.

функция

Рисунок 2.2 – Диаграмма

ступенчатая

отображает

включение

постоянного

функции 1(t)

напряжения, равного 1В (или постоянного

тока, равного 1 А) в момент t = 0.

Согласно (2.1) изображение единичной ступенчатой функции имеет вид:

∞

−pt

∞

F( p) = ∫1(t)e−pt dt = e

− p

Следовательно

1(t)

(2.2)

Изображение постоянной А, возникающей в момент времени t = 0, легко найти, если представить ее с помощью единичной функции, как f(t) = A·1(t)

Тогда

f(t) = A·1(t) А/р.

(2.3)

Показательная функция [f(t) = eαt].

Умножение любой функции времени на единичную функцию оставляет первую без изменения при t > 0 и дает нулевое значение при t < 0.

Так, умножив показательную функцию eat на единичную функцию, получают функцию оригинал

	at	при t > 0,
f (t) = e		при t > 0,
0		при t < 0.

Пусть а – произвольное число. Тогда изображение этого оригинала

∞		−( p−a)t	∞

F( p) = ∫eat e−pt dt = −e
0	( p − a)		0

= p 1− a .

Следовательно:	1
eat		.	(2.4)
	p − a

Полученное выражение справедливо так же для действительных и мнимых значений а.

Операциям над оригиналами соответствуют операции над изображениями и наоборот. Применение свойств преобразования Лапласа существенно упрощает эти операции (особенно на этапе определения искомого оригинала по вычисленному изображению). Основные свойства преобразования Лапласа, известные из курса математического анализа, достаточно широко приведены в рекомендованной литературе. Далее будут рассмотрены те из свойств, которые используются при анализе электрических цепей.

1 Умножение функции времени f(t) на постоянное число А соответствует

умножению на это же число ее изображения:
A f (t) A F( p).	(2.5)

2 Изображение линейной комбинации оригиналов есть линейная комбинация изображений:

∑ak fk (t)

k =1

n
∑ak Fk ( p).	(2.6)

k=1

При анализе переходных процессов особенно важны преобразования, связанные с дифференцированием и интегрированием оригиналов (теоремы дифференцирования и интегрирования).

3 По теореме дифференцирования:

′	pF( p) − f (0) .	(2.7)
f (t)	pF( p) − f (0) .	(2.7)
В случае, когда оригинал	в начальной точке непрерывен,	т. е.

f(0) = f(0–) = 0, его дифференцированию соответствует операция умножения изображения на р:

′	(2.8)
f (t) pF( p).

Повторное применение операции, выраженной формулой (2.8), дает изображение производных функции f(t) высших порядков, т. е. n – кратному дифференцированию оригинала соответствует n – кратное умножение изображения на р (если все производные при t = 0 равны нулю):

			28
f n (t) pn F( p).			(2.9)
4 По теореме интегрирования:
t	F( p)
∫ f (t)dt	F( p)	.	(2.10)
∫ f (t)dt		.	(2.10)
0	p

Повторное применение операции, выраженной формулой (2.10), дает:

t	t			n
∫	∫			n
	...	f (t)(dt)n	F( p)		.	(2.11)
	...	f (t)(dt)n			.	(2.11)
0	0		p

Согласно теореме дифференцирования и интегрирования комплексную переменную р можно рассматривать как оператор (отсюда название

операторный метод).

5 По теореме запаздывания (смещения в области действительного переменного):

f (t −tз) e−ptз F( p).

(2.12)

Из (2.12) следует, что умножение изображения на e –ptз сдвигает оригинал

f(t) по оси времени вправо на tз.

6 Теорема смещения (смещение в области комплексного переменного)

e±αt f (t) F( p mα).

(2.13)

Умножение оригинала на показательную функцию e±αt соответствует смещению изображения на комплексной плоскости на mα. При этом α может быть как действительным, так и комплексным.

7 Теорема умножения изображений (теорема свертывания)

tk
F1( p) F2 ( p) ∫ f1(x) f2 (tk − x)dx.	(2.14)

x=0

Из (2.14) следует, что умножению в области комплексного переменного соответствует свертывание в области действительного переменного.

8 Предельные соотношения:

– начальное значение оригинала:

lim f (t) = lim pF( p) ;		(2.15)
t→0	p→∞
– конечное значение оригинала:	f (t) = lim pF( p).
lim	f (t) = lim pF( p).	(2.16)
t→∞	p→0

Предельные соотношения (2.15) и (2.16) используются для проверки вычислений с помощью преобразований Лапласа.

2.2 Обратное преобразование Лапласа. Теорема разложения

Решение интегрального уравнения (2.1) относительно функции f(t) дает обратное преобразование Лапласа:

				29
	1	σ + j∞
f (t) =	1	0	∫F( p)e pt dp.	(2.17)
f (t) =	2πj		∫F( p)e pt dp.	(2.17)
	2πj		− j∞
		σ0	− j∞

При использовании обратного преобразования Лапласа (2.17) были получены оригиналы некоторых изображений. Они приводятся в справочниках по операционному исчислению, в рекомендованной литературе и содержат пары оригинал-изображение.

Фрагмент такой таблицы для наиболее часто используемых при анализе функций приведен ниже (таблица 2.1). Данные таблицы 2.1 будут использованы далее при решении примеров анализа ПП операторным методом.

Таблица 2.1 – Таблица преобразований Лапласа (фрагмент)

№

f(t) – оригинал

F(p) – изображение

A(t) = const

Aemat

p ± a

(1 − e−at )

p( p + a)

(e−вt − e−at )

( p + a)( p + в)

a −в

sin ω0t

ω0

+ ω0

Теорема разложения.

Для нахождения оригинала f(t) по изображению F(p) можно воспользоваться таблицами, если изображение достаточно простое и имеется в таблицах. Если же полученное в результате анализа операторным методом изображение отсутствует в таблицах, то его находят при помощи теоремы разложения. Обычно такие изображения, представляют собой дробнорациональные функции.

Дробно-рациональными функциями называются функции комплексной

переменной р с вещественными коэффициентами:

M ( p) =

pm + b

p(m−1) +... + b p +b

F ( p) =

(m−1)

(2.18)

N ( p)

an pn + a(n−1)p(n−1) +... + a1 p + a0

Любая дробно-рациональная функция может быть представлена

следующим образом:

pm +b

(m−1) +... +b p +b

M ( p) =

F ( p) =

(m−1)

(2.19)

N ( p)

( p − p1 )( p − p2 )...........( p − pn )

Пусть изображение по Лапласу F(p) некоторой искомой функции f(t) является правильной дробно-рациональной функцией с вещественными

коэффициентами и простыми полюсами. Тогда функция F(p) может быть единственным образом разложена на сумму простых дробей:

F( p) =	A1	+	A2		+.... +	An		.	(2.20)
F( p) =	p − p	+	p − p		+.... +			.	(2.20)
	p − p		p − p	2		p − p	n
	1			2			n
Оригиналом этого изображения (см. строку 2 табл. 2.1) является сумма
экспоненциальных функций:
f (t) = A e p1t + A e p2t +... + A e pnt .									(2.21)
	1		2			n

Определение коэффициентов А1, А2, …, Аn предлагается проследить на примере получения коэффициента А1. Для этого обе части выражения (2.20) умножаются на (р - р1).

Тогда

				A2			An
( p − p1 )F( p) = A1 +				A2	+	... +	An

			( p − p1 )					.
При р → р1			p − p2				p − pn
При р → р1	= lim ( p − p )F( p) = lim ( p − p ) M ( p) .
A	= lim ( p − p )F( p) = lim ( p − p ) M ( p) .
1	p→p1	1	p→p1		1	N( p)

Впоследнем выражении множитель (р - р1) и знаменатель N(p) одновременно стремятся к нулю при р → р1. Эта неопределенность раскрывается по правилу Лопиталя.

Врезультате:

		d		( p − p		)
				( p − p		)
A = M ( p )		dp			1		=	M ( p1 )	.
		dp						M ( p1 )

1	1		d		N ( p)			N ′( p1 )
			d					N ′( p1 )
			dp				p=p1
							p=p1

Очевидно, что любой другой коэффициент будет определяться выражением:

Ak = M′( pk ) . N ( pk )

Следовательно, оригинал (некоторая искомая функция тока или напряжения) будет иметь вид:

M ( p

)

p t

f (t) = ∑

e k

(2.22)

′

k=1

N ( pk )

Учитывая соответствие выражений (2.19) и (2.22), можно записать:

M ( p)

bm p

+b(m−1)p

(m−1)

+... +b0

M ( pk )

∑

e pkt .

(2.23)

N( p)

αn pn + α(n−1)p(n−1) +... + α0

k=1

N ′( pk )

Если знаменатель функции F(p) имеет один корень, равный нулю, то

оригинал f(t) находится следующим образом:

e pkt

(2.24)

M ( p) = M ( p)

M (0) + ∑ M (′pk )

N( p)

pN1 ( p)

N(0)

k=1

pk N ( pk )

В литературе зачастую выражения (2.23) и (2.24) называют формулами разложения.

2.3 Законы теории электрических цепей в операторной форме. Схемы замещения двухполюсных элементов

Так как сумме функций оригиналов соответствует сумма изображений этих функций, то от записи уравнений по законам Кирхгофа, составленных для мгновенных значений токов и напряжений (оригиналов), легко перейти к записи уравнений по тем же законам для изображений токов и напряжений.

N
∑Ik ( p) = 0	(2.25)
k =1
и
N
∑Uk ( p) = 0 .	(2.26)

k =1

Выражения (2.25) и (2.26) называют законами Кирхгофа в операторной форме. По аналогии с понятиями комплексного входного сопротивления Z(jω) и комплексной входной проводимости Y(jω) вводится понятие операторного входного сопротивления Z(р) и операторной входной проводимости Y(р).

Операторным входным сопротивлением пассивного линейного двухполюсника называется отношение операторного изображения напряжения на входе двухполюсника к операторному изображению входного тока при нулевых начальных условиях

Z( p) =	U ( p)	.	(2.27)

	I ( p)

Вдальнейшем вместо „операторное изображение тока (напряжения)” будет использоваться термин „изображение”.

В(2.27)

I ( p) i(t)

U ( p) u(t)

– изображение тока и напряжения на входе некоторого пассивного двухполюсника при t ≥ 0. Величина, обратная Z(р) является операторной входной проводимостью двухполюсника

Y ( p) =	1	=		I ( p)	.	(2.28)
	Z( p)
			U ( p)

Операторные схемы замещения идеальных двухполюсных элементов

цепи зависят от начальных условий цепи.

При нулевых начальных условиях цепи каждый пассивный линейный двухполюсник (R, L или C) представляется своим операторным входным сопротивлением Z(p) или операторной входной проводимостью Y(p).

В таблице 2.2 представлены операторные схемы замещения идеальных резисторов, емкостей и индуктивностей при нулевых начальных условиях цепи.

Таблица 2.2 – Закон Ома для элементов R, L, C при нулевых начальных условиях

Элементы после

Z(p)

Y(p)

U(p)

I(p)

коммутации

R, G

IR(p)·R

UG(p)·G

1 / pL

IL(p)·pL

UL(p)·(1 / pL)

iС

1 / pC

IC(p)·(1 / pC)

UC(p)·pC

uС

Z(p)

Y(p)

I(p)·Z(p)

U(p)·Y(p)

Рассмотрим операторные схемы замещения идеальных емкостей и индуктивностей, которые находятся в цепях с ненулевыми начальными условиями. В этом случае операторные схемы замещения емкости и индуктивности должны содержать независимые источники напряжения или тока, отражающие начальный запас энергии в цепи.

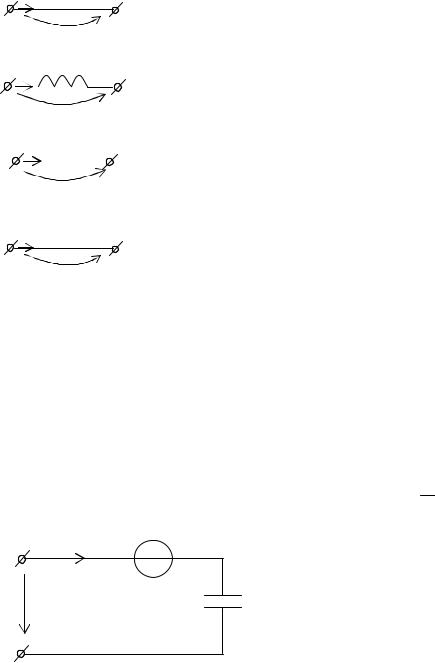
Емкость. Мгновенные значения тока и напряжения емкости связаны соотношениями:

		iC (t) = C			duC (t)	;
		iC (t) = C			dt	;
					dt
IC(p)	+		uC (0) / p
+
UC(p)	ZC	( p) =		1
UC(p)	ZC	( p) =		pС
				pС

Рисунок 2.3 – Операторная схема замещения заряженной емкости с источником напряжения

1 t

uC (t) = uc (0) + C ∫0 iC (t)dt ,

где uC (0) ≠ 0 .

Применив теоремы дифференцирования (2.7) и интегрирования (2.10), получаем

IC ( p) = pCUC ( p) −CuC (0). (2.29)

UC ( p) =	uC (0)	+	1	IC ( p), (2.30)
	p		pC

По структуре формулы (2.30) можно изобразить операторную схему замещения емкости при ненулевых

начальных условиях (рис. 2.3).

Схема, изображенная на рис. 2.3, представляет собой последовательное соединение „незаряженной” емкости (емкости при нулевых начальных условиях) со своим операторным сопротивлением ZC ( p) и идеального

независимого источника напряжения с задающим напряжением, равным uC (0) / p .

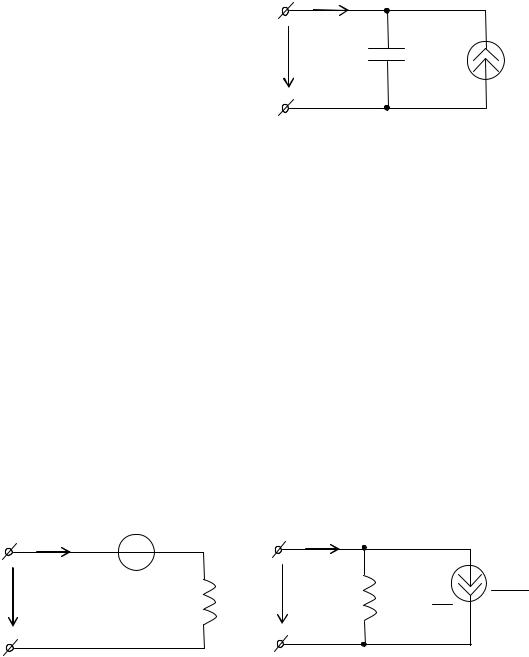
Уравнению (2.29) соответствует операторная схема замещения емкости

(рис.

2.4),

представляющая

парал-

IC(p)

лельное соединение “незаряжен-

ной” емкости и идеального

UC(p)

независимого источника

тока

YC(p) = pC

CuC(0)

задающим током, равным C uC (0) .

Индуктивность.

Мгновенные

значения

тока и

напряжения

Рисунок 2.4 – Операторная схема

индуктивности в цепи с ненуле-

замещения емкости с источником тока

выми

начальными

условиями

связаны соотношениями:

(t)

1 t

(t) = L

, iL (t) = iL (0)

uL (t)dt,

∫0

где iL (0) ≠ 0 .

Применив теоремы дифференцирования (2.7) и интегрирования (2.10), получаем:

UL ( p) = pL IL ( p) − LiL (0) ,					(2.31)
IL ( p) =	iL (0)	+	1	uL ( p) .	(2.32)
	p		pL

По структурам формул (2.31) и (2.32) можно изобразить соответственно две операторные схемы замещения индуктивности при ненулевых начальных условиях (рис. 2.5 и 2.6).

Обе схемы содержат “незаряженной” индуктивности и независимые идеальные источники.

LiL(0)

+	IL(p)	+
		+

UL(p)		ZL ( p) = pL	UL(p)
		ZL ( p) = pL

IL(p)

	1	iL (0)
YL ( p) =	1	p
	pL

Рисунок 2.5 – Операторная схема	Рисунок 2.6 – Операторная схема
замещения индуктивности с	замещения индуктивности с
источником напряжения	источником тока

Используя операторные схемы замещения идеальных пассивных элементов (R, L, C), можно построить операторную схему замещения произвольной цепи. При этом в операторной схеме замещения содержатся дополнительные источники энергии, характеризующие запас энергии в реактивных элементах (L, C) в момент времени t(0–), непосредственно предшествующий коммутации.

<<< < Предыдущая 1 2 3 45 / 135 6 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.02.2016609 Кб13МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУК2 - копия.docx
#
06.09.2019370.69 Кб3МК з підприємницької практики.doc
#
10.02.201651.2 Кб15Модель OSI.doc
#
10.02.20161.56 Mб94Модуль 1.pdf
#
10.02.20161.61 Mб171Модуль 2.pdf
#
10.02.20161.56 Mб133Модуль 3.pdf
#
10.02.20161.39 Mб38Модуль 4.pdf
#
24.08.201975.66 Кб10модульна робота.docx
#
10.02.2016128.8 Кб33Московский Педагогический коледж.docx
#
19.11.2018165.89 Кб9МР к ЛР 1.0 рус.doc
#
19.11.2018168.45 Кб4МР к ЛР 1.0 укр.doc