10.2 Понятие об аппроксимации

Одновременно с задачей интерполяции результатов экспериментов – значений функции, которая задана в узлах, широко распространена задача построения регрессии или аппроксимации результатов некоторой заранее известной функцией y(x). Вид этой функции определяется особенностями решаемой задачи, например, физическими соображениями, если производится аппроксимация результатов физического эксперимента. Параметры этой функции должны находиться из следующего очевидного условия – среднеквадратичные отклонения аппроксимирующей функции от ее значений в узлах должны быть минимальны. Таким образом в основе процедуры аппроксимации лежит метод наименьших квадратов – МНК. Очевидно, что при аппроксимации не требуется, чтобы аппроксимирующая функция проходила через все заданные точки, что особенно важно при аппроксимации данных, заведомо содержащих погрешности, т.е. аппроксимирующая кривая проходя между точками – сглаживает погрешности измерений.

Если исходные данные содержат значительные погрешности («шумы»), то перед проведением аппроксимации рекомендуется их предварительно сгладить. Чаще всего для сглаживания применяется метод скользящего среднего, в соответствии с которым каждый из экспериментальных значений пересчитывается по формуле

, (10.2)

где величина определяет ширину окна сглаживания. В некоторых случаях слагаемые в сумме (10.2) входят с различным весом.

Наиболее часто встречается простейший вариант МНК – аппроксимация прямой линией (линейная аппроксимация или линейная регрессия), при которой аппроксимирующая функция имеет вид

. (10.3)

Набор экспериментальных точек может быть аппроксимирован и полиномиальной зависимостью, т.е. полиномом n-ой степени

(10.4)

Часто процедура аппроксимации может быть сведена к задаче построения линейной регрессии путем замены переменных. Проиллюстрируем процедуру линеаризации на следующем примере. Пусть аппроксимирующая функция ищется в виде:. Прологарифмируем это выражение и введем обозначения ,. Тогда в новых обозначениях задача сводится к отысканию коэффициентов линейной функции:.

Иногда экспериментальные данные удобно аппроксимировать комбинацией функций. Если функции изаданы, то процедура аппроксимации заключается в том, чтобы отыскать методом наименьших квадратов значения коэффициентовдля комбинации функций

, (10.5)

которые приближают экспериментальные данные наилучшим образом.

10.3. Реализация процедур локальной интерполяции и аппроксимации в пакете MathCad

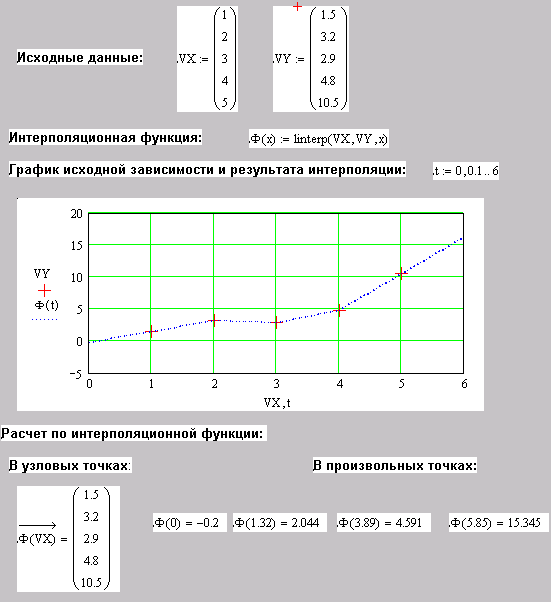
Для проведения линейной интерполяции в пакете MathCAD используется встроенная функция linterp(vx,vy,z), которая использует векторы данных аргумента (vx) и функции (vy), чтобы возвратить интерполируемое значение, соответствующее третьему аргументу z. Аргументы vx и vy должны быть векторами одинаковой длины, причем вектор vx должен содержать вещественные значения, расположенные по возрастанию (если это не так, то их необходимо вначале упорядочить).

Рис. 10.3 Процедура проведения кусочно-линейной интерполяции

Если величина z, расположена перед первой (или за последней) точкой в векторе vx, то MathCAD продолжает ломаную прямой линией, проходящей через первые две (последние две) точки данных. На рис. 10.3 приведен фрагмент MathCAD документа в котором проводится линейная интерполяция табличной зависимости. Исходная зависимость задается векторами VX и VY (по 5 точек). Затем определяется интерполяционная функция Ф(х), которая позволяет для любого значения аргумента определить искомую величину функции. График этой функции представлен на рис. 10.3 (пунктир) совместно с узловыми точками (крестики). Как видно из рис. 10.3 в узловых точках значения интерполируемой функции совпадают с табличными.

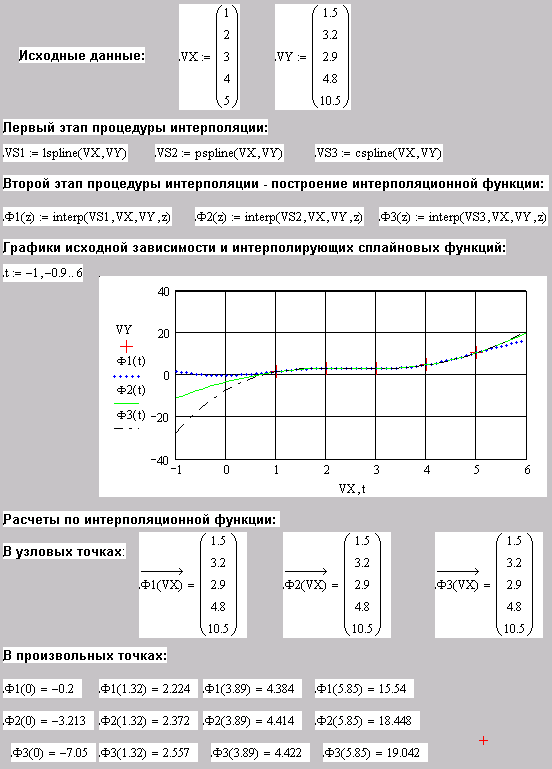
Рис. 10.4. Процедура проведения сплайновой интерполяции.

Сплайновая интерполяция в пакете Mathcad проводится в два этапа – на первом этапе определяется вектор вторых производных интерполирующей функции VS посредством одной из трех функций lspline(vx,vy), pspline(vx,vy), cspline(vx,vy). На втором этапе этот вектор используется в функции interp(vs,vx,vy,z), которая возвращает интерполируемое значение, соответствующее аргументу z. Вышеперечисленные три функции кубической сплайновой интерполяции соответствует заданию линейных, квадратичных (параболических) или кубических условий на границах интервала, а аргументы vx и vy удовлетворяют тем же требованиям, что и в случае линейной интерполяции. Пример проведения процедуры сплайновой интерполяции дан на рис. 10.4. Как видно из рис. 10.4 поведение интерполирующих зависимостей практически одинаково (с незначительными отличиями) внутри интервала задания исходных данных, но значительно отличается вне его.

При выполнении линейной аппроксимации необходимо найти значения коэффициентов прямой иуравнения (10.3). Для их определения используются встроенные функции slope(VX,VY) (англ. наклон), которая определяет угловой коэффициент прямой и intercept(VX,VY) (англ.: отложить отрезок на линии), которая определяет точку пересечения графика с вертикальной осью. Кроме того, может применяться функция line(VX,VY), которая определяет оба параметра прямой одновременно в виде вектора. Применение этих процедур иллюстрируется на рис. 10.5, который представляет собой фрагмент документа Mathcad.

Рис. 10.5. Построение линейной регрессии.

Здесь, одновременно с параметрами линейной регрессии, вычисляются коэффициент корреляции (связи) двух множеств и среднеквадратичное отклонение (СКО) точек исходного дискретного множества от функции линейной регрессии. Чем величина модуля коэффициента корреляции ближе к единице и чем меньше величина СКО, тем теснее связь между данными множествами.

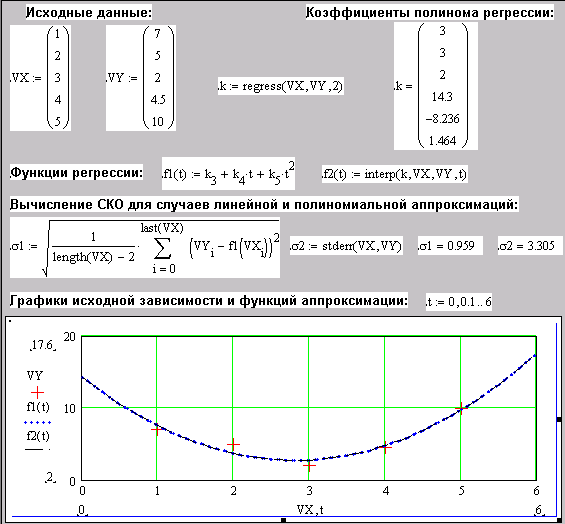
При аппроксимации полиномиальной зависимостью следует выполнить два этапа. Вначале встроенная функция regress(VX,VY,n) возвращает вектор (назовем его k), элементы которого, начиная с четвертого. Представляют собой коэффициенты аппроксимирующего полинома формулы (10.4). Эта же формула может быть использована для построения аппроксимирующей функции, однако, однако эту функцию удобнее получить иначе – использовав весь вектор значений k в функции f(x)= interp(k,X,Y,x).

Пример выполнения полиномиальной аппроксимации представлен на рис. 10.6. Здесь же показано вычисление величины СКО для случаев полиномиальной и линейной аппроксимаций. Как видно из представленных на рисунке вычислений, величина СКО для случая аппроксимации параболой заметно меньше, чем для линейной аппроксимации.

Рис. 10.6. Проведение полиномиальной аппроксимации.

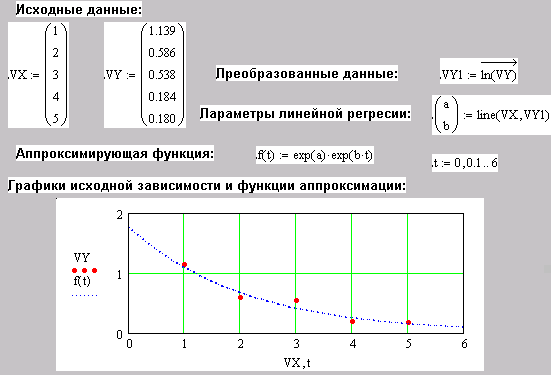
Решение задачи линеаризации исходной функции путем замены переменных проиллюстрирована во фрагменте документа Mathcad, который представлен на рис. 10.7.

Рис. 10.7. Аппроксимация методом линеаризации исходной зависимости

На рис. 10.8 приведен фрагмент документа MathCAD в котором производится аппроксимация линейной комбинацией двух функций () в соответствии с формулой (10.5). В этом случае используется функцияlinfit, которая имеет три аргумента: вектор VX – абсциссы заданных точек, вектор VY – ординаты заданных точек и функция F – содержит набор функций, используемый для построения линейной комбинации.

Рис. 10.8. Аппроксимация линейной комбинацией функций

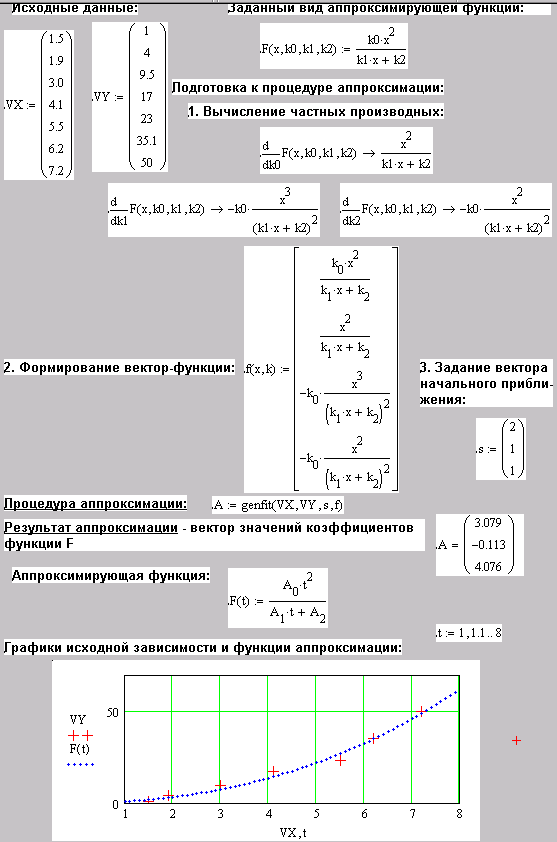
Для нахождения выражения для аппроксимирующей функции общего вида используется функция genfit(VX,VY,s,F). Она имеет следующие параметры: VX, VY – векторы, содержащие координаты заданных точек, f – функция, задающая искомую функциональную n–параметрическую зависимость и частные производные этой зависимости по этим параметрам, s – вектор, задающий начальные приближения для поиска параметров.

Аппроксимация экспериментальных результатов функцией общего вида проиллюстрирована на фрагменте MathCAD документа приведеного на рис. 10.9. В качестве аппроксимирующей функции выбрано выражение . При этом, хотя выражения для производных можно вычислить «врукопашную», будем использовать возможности символьного блока пакетаMathCAD. Заметим, что результат вычисления коэффициентов существенно зависит от выбора начального приближения .

Рис. 10.9. Проведение аппроксимации функцией общего вида:

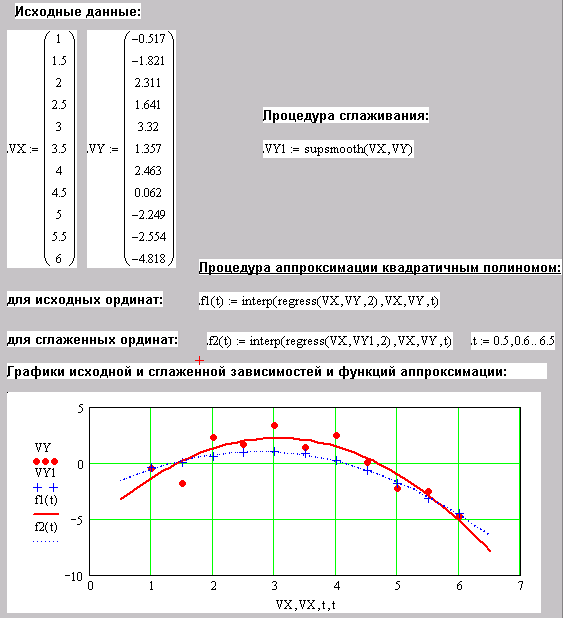
Для сглаживания результатов Mathcad предоставляет три функции – medsmooth(VY,n) (возвращает усредненные значения вектора ординат сглаживанием с помощью скользящего окна шириной n, которое должно являться нечетным числом), ksmooth(VX,VY,b) (возвращает усредненные значения вектора ординат сглаживанием с помощью процедуры с гауссовым ядром с шириной b) и supsmooth(VX,VY,) (возвращает усредненные значения вектора ординат сглаживанием с помощью кусочно-линейной процедуры с окном адаптивно изменяющейся ширины). В зависимости от ситуации наиболее эффективным является тот или иной метод. Пример процедуры построения аппроксимирующей зависимости с проведением процедуры предварительного сглаживания представлен на рис. 10.10.

Рис. 10.10. Проведение аппроксимации с предварительным сглаживанием