9. Методы решения систем уравнений
Задачи инженерной практики зачастую сводятся к необходимости решения не одного уравнения, а систем связанных уравнений. Эти системы уравнений могут быть линейными и нелинейными, с постоянными или с переменными коэффициентами. Решение их возможно точными (аналитическими, символьными) и приближенными (численными) методами. Первые – дают решение в общем виде, что, в силу общности и удобства анализа полученного результата, всегда более предпочтительно. Однако, набор систем уравнений, который может быть решен аналитическими методами, крайне ограничен. Эти методы пригодны лишь для решения систем линейных алгебраических уравнений и, в редких случаях, для решения систем нелинейных уравнений невысокого порядка.
Численные методы позволяют, в принципе, получить решение любых систем уравнений (как линейных, так и нелинейных) с заданной точностью путем организации сходящихся итерационных процессов.
9.1. Точные методы решения систем уравнений и реализация их в пакете MathCad
Рассмотрим систему n линейных алгебраических уравнений относительно неизвестных х1, х2, …, хn:
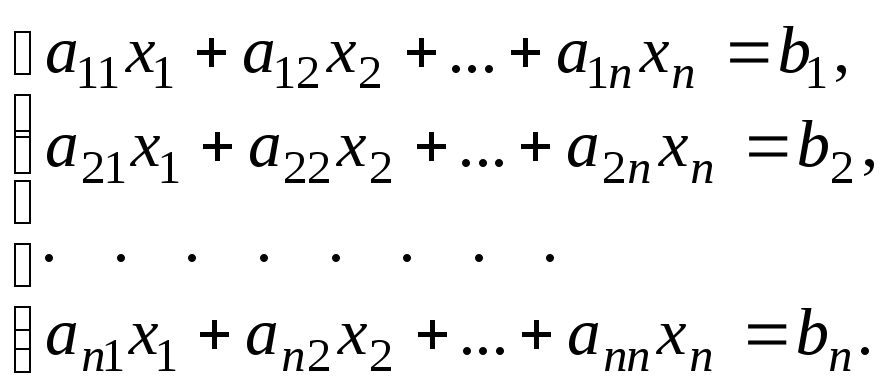(9.1)
Здесь, ai,j – коэффициенты в i-ом уравнении при j-ом неизвестном, bi –свободные члены.
Система уравнений называется совместной, если она имеет, хотя бы одно решение, при этом совместная система может иметь единственное решение или бесконечное множество решений. В последнем случае систему называют неопределенной.
В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричной форме в виде
Ах = b, (9.2)
где введены следующие обозначения:
.
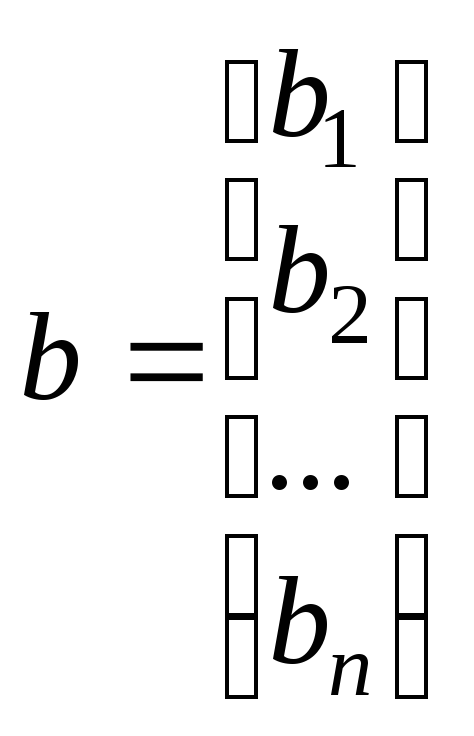(9.3)
Матрица А называется матрицей системы, матрица-столбец b – матрицей (вектором) правой части, а матрица-столбец х, – вектором решения системы. Очевидно, что число строк квадратной матрицы A и вектора b должно совпадать.
Если матрица А является невырожденной (т.е. ее определитель det A 0), то существует обратная матрица А-1 и, умножая обе части уравнения (3.3) на неё, получим выражение для решения системы, которое является единственным:
(9.4)
Пакет MathCADпозволяет сформировать обратную матрицу и получить решение (4.4) непосредственно, а также, используя для этой цели встроенную функциюlsolve(A,b).
Альтернативным способом решения системы уравнений является метод исключений Гаусса. Он состоит в том, что систему (9.1) приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей:
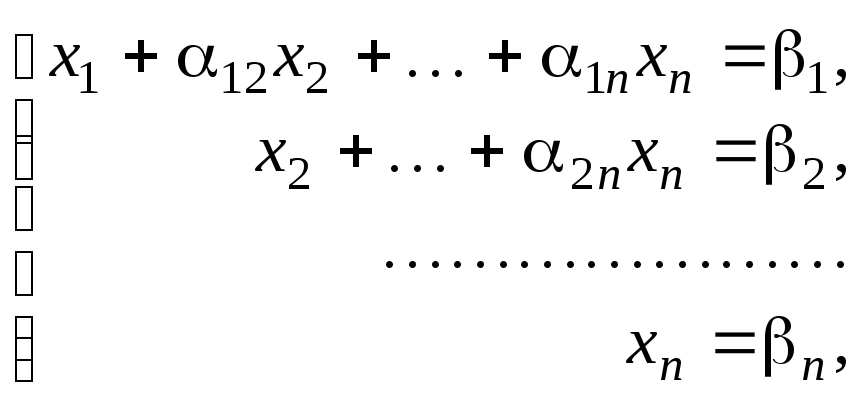(4.5)
решение которой может быть найдено по рекуррентным формулам:
(4.6)
В матричной записи метод Гаусса сводится к преобразованию расширенной матрицы эквивалентной системы, которая получена объединением матриц системы и вектора правой части к такому виду, чтобы в первых n столбцах получилась единичная матрица, тогда последний, (n + 1) столбец этой матрицы и будет содержать решение системы (9.1).
Напомним, что в пакете MathCAD формирование расширенной матрицы С производится с помощью встроенной функции augment (A,b) (число строк у A и b должно совпадать), а процедуру ее преобразования (т.н. прямой и обратный ходы метода Гаусса) выполняет встроенная функция rref(С). Затем вектор решения можно выделить как последний столбец преобразованной матрицы. Ниже приведен фрагмент документа MathCAD, в котором проиллюстрировано применение различных точных методов решения систем уравнений:
Рис. 9.1. Реализация точных методов решения систем уравнений в пакете MathCAD
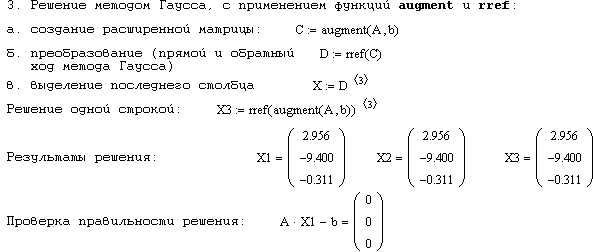
Рис. 9.2. Реализация точных методов решения систем уравнений в пакете MathCAD
Как уже отмечалось выше, аналитическая форма решения уравнений представляется более удобной для анализа результатов, поскольку может выразить корни через параметры, входящие в уравнения системы. Поэтому, вместо того, чтобы решать уравнение для каждого нового значения параметра, можно просто заменять его значение в найденном решении.
Решение в аналитической форме (symbolic) удобно производить внутри блока решений, который, как и ранее, открывается ключевым словом Given. Ниже его в любом порядке печатаются уравнения, причем для ввода знака = используется знак «жирного» равенства [Ctrl]=. Завершает блок функция Find, аргументами которой являются искомые переменные, входящие в состав системы. Для того, чтобы эта функция возвратила аналитическое решение системы уравнений необходимо поместить за ней символьный знак равенства ..
Внутри блока решения выражения недопустимыми является следующие выражения:
ограничения со знаком ;
дискретный аргумент или выражения, содержащие дискретный (ранжированный) аргумент в любой форме;
сложные неравенства вида a < b < c.
Блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find.
Вместе с тем решение системы уравнений в аналитической форме может быть получено и с помощью рассмотренного ранее матричного метода, в котором следует считать матрицу системы и вектор правой части зависящими от параметров системы уранений.
Пример символьного решения системы уравнений представлен в нижеследующем фрагменте документа MathCAD.
Рис. 9.3. Аналитическое решение системы линейных уравнений