
ЛЕКЦИЯ_1 / Основы теории автоматического управления - УП - Лазарева-Мартемьянов - 2004 - 352
.pdf
(a sn +a |
sn−1 + ...+a s +a )y(s) =(b sm +b |
sm−1 + ...+b s +b )x(s), (4.7) |
||||
n |
n−1 |
1 |
0 |
m |
m−1 |
1 0 |
∞
где y(s) = ∫y(t)e−st dt – преобразование Лапласа функции y(t).
0
∞
Преобразование Фурье функции y(t) определяется выражением y(iω) = ∫y(t)e−iωt dt , причем должны
0
∞
выполняться условия, что y(t) = 0 при t < 0 и ∫y(t)dt существует.
0
Сравнивая преобразования Лапласа и Фурье, видно, что формально оно может быть получено из преобразования Лапласа простой заменой s на iω, но из-за второго условия преобразование Фурье выполняется для более ограниченного класса функций. Заменяя в уравнении (4.9) s на iω, получаем:
(a |
(iω)n + a |
n−1 |
(iω)n−1 + ... + a (iω) + a |
)y(iω) = |
|
|
|
|
|
|
||||||
n |
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
= (b (iω)m + b |
|
(iω)m−1 |
+ ... + b (iω) + b )x(iω), |
|
|
|
|
|
|
|||||||
|
m |
m−1 |
|
|
1 |
|
0 |
|
|
|
|
|
|
|
||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(iω) |
|
|
b |
(iω)m + b |
|
(iω)m−1 + ... + b |
(iω) + b |
. (4.8) |
||
|
|
|
|
W |
(iω) = |
|
= |
|
m |
|
m−1 |
1 |
|
0 |
||
|
|
|
|
y(iω) |
a |
(iω)n + a |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
n−1 |
(iω)n−1 + ... + a (iω) + a |
0 |
|
|||||
|
|
|
|
|
|
|
|
|
n |
|
|
1 |
|
|
||
Проводя анализ выражения (4.8), можно записать, что
|
B(ω) + i B (ω) |
|
M |
ч |
(ω)eiϕЧ(ω) |
W (iω) = |
1 |
= |
|
|
|
A(ω) + i A1(ω) |
M зн(ω)eiϕЗН(ω) |
||||
и сделать вывод: амплитудно-частотная характеристика M (ω) = M ч(ω)
M зн(ω)
является четной функцией; фазо-
частотная характеристика ϕ(ω) = = ϕч( ) – ϕзн(ω) – нечетной функцией; вещественная частотная характеристика Re(ω) – четной функци-
ей; мнимая частотная характеристика Im( ) – нечетной функцией (рис. 4.6 и 4.7).
M |
a) |
Re |
б) |
ω |
|
ω |
Рис. 4.6 Свойство четности частотных характеристик:
а – АЧХ; б – ВЧХ
ϕ |
а) |
Im |
б) |
ω |
|
ω |

Рис. 4.7 Свойство нечетности частотных характеристик:
а – ФЧХ; б – МЧХ
Амплитудно-фазовая характеристика также может рассматриваться как изображение Фурье от весовой функции:
∞ |
|
W (iω) = ∫w(t)e−iωt dt . |
(4.9) |
0
Так как e−iωt = cosωt − isinωt , то из (4.9) могут быть получены формулы для определения вещественной и мнимой характеристик:
∞
W (iω) = ∫w(t){cosωt −i sinωt}dt ,
0
и, следовательно,
∞ |
|
Re(ω) = ∫w(t)cosωtdt , |
(4.10) |
0 |
|
∞ |
|
Im(ω) = −∫w(t)sin ωtdt . |
(4.11) |
0 |
|
Из последних формул следует, что |
|
Re(ω) = Re(−ω), Im(ω) = −Im(−ω) , |
(4.12) |
А ЭТО СВИДЕТЕЛЬСТВУЕТ О ТОМ, ЧТО АФХ ПРИ ОТРИЦАТЕЛЬНЫХ ЧАСТОТАХ ЯВЛЯЕТСЯ ЗЕРКАЛЬНЫМ ОТОБРАЖЕНИЕМ АФХ ДЛЯ ПОЛОЖИТЕЛЬНЫХ ЧАСТОТ ОТНОСИТЕЛЬНО ВЕЩЕСТВЕННОЙ ОСИ (РИС. 4.8).
При практических расчетах обычно ограничиваются построением АФХ только для положительных частот. Используя формулу обратного преобразования Фурье, можно по АФХ получить весовую характеристику:
|
|
|
|
|
|
1 |
|
∞ |
|
|
|
|
|
w(t) = |
|
∫W (iω)eiωt dω. |
(4.13) |
||||
|
|
|
2π |
|||||||
|
|
|
|
|
|
−∞ |
|
|||
|
|
|
|
|
|
|
|
|
||
Пример 4.1 Пусть задана передаточная функция объекта W (s) = |
|
|
e−s |
|
||||||
|
, требуется определить час- |
|||||||||
s2 + 2s +3 |
||||||||||
тотные характеристики. |
|
|
|
|
|
|
|
|
||
Заменяя s на iω, записываем выражение для АФХ: |
|
|
|
|
|
|
|
|
||
|
e−iω |
e−iω |
|
|
|
|
|
|||
W (iω) = |
|
= |
|
. |
|
|
|
|
|
|
(iω)2 + 2(iω) +3 |
(3−ω2) + 2iω |
|
|
|
|
|
||||
Так как рассматриваемый объект линеен и стационарен, то, применяя принцип суперпозиции, име-
ем:
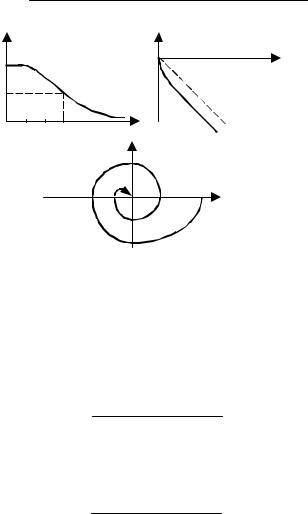
АЧХ (рис. 4.9, а) M (ω) = |
1 |
; |
|
(3−ω2)2 + 4ω2 |
|||
|
|
ФЧХ (рис. 4.9, б) ϕ(ω) = −ω− arctg 3 −2ωω2 .
Годографамплитудно-фазовойхарактеристикиизображеннарис. 4.9, в.
Вещественную и мнимую частотные характеристики обычно получают умножением числителя и знаменателя на выражение, сопряженное знаменателю:
W (iω) = |
|
e−iω |
= |
cos ω−i sin |
ω |
|
(3 |
−ω2 ) − 2iω |
= |
|
|
−ω2 ) + 2iω |
(3 |
−ω2 ) + 2iω |
(3 |
−ω2 ) − 2iω |
|||||
(3 |
|
|
|
|||||||
|
= |
(3−ω2 )cosω− 2ωsin ω−i((3 |
−ω2 )sin |
ω+ 2ωcosω) |
, |
|||
|
|
|
(3−ω2 )2 + |
4ω2 |
|
|||
|
|
|
|
|
|
|||
M |
|
|
|
а) |
ϕ |
|
б) |
|
|
|
|
|
|
|
|
|
|
1/3 |
|
|
|
|
0 |
|
ω |
|
|
|
|
|
|
|
|
||
1/6 |
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
ω |
|
|
|
|
|
|
|
|
|
i Im(ω) |
в) |
|
|
|
|
|
|
ω→∞ |
|
1/3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω= 0 Re(ω) |
|
|
|
Рис. 4.9 Графики частотных характеристик:
а – АЧХ; б – ФЧХ; в – АФХ
откуда
– вещественно-частотная характеристика:
Re(ω) = (3 − ω2 )cosω − 2ωsinω;
(3 − ω2 )2 + 4ω2
– мнимая частотная характеристика:
Im(ω) = (3 − ω2 )sin ω+ 2ωcosω .
(3 − ω2 )2 + 4ω2
4.4 Связь дифференциального уравнения с частотными характеристиками
Решение дифференциального уравнения (3.36, а) имеет вид
y(t) = yсв(t) + yвын(t) , |
(4.14) |
где yвын(t) – вынужденное движение, описываемое частным решением; yсв(t) – свободные движения, описываемые общим решением однородного уравнения.
Для установления связи между АФХ и дифференциальным уравнением рассматриваются вынужденные движения при входном гармоническом воздействии вида: x(t) = 2А cosωt, которое можно представить по формуле Эйлера x(t) = Aeiωt + Ae−iωt и рассматривать как сумму входных сигналов, т.е.
x(t) = x1(t) + x2(t) .
В этом случае частное решение дифференциального уравнения в силу принципа суперпозиции также представляется в виде суммы
yвын(t) = yвын1 (t) + yвын2 (t) ,
где |
yвын1 (t)и yвын2 (t) определяются соответственно видом x1(t) и x2(t). В связи с этим решения будут ис- |
||||||||||
каться в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yвын (t) = AW (iω)eiωt ; |
yвын (t) = AW (−iω)e−iωt , |
|
|
|
||||
|
|
|
|
1 |
2 |
|
|
|
|
|
|
где |
W(iω), |
W(−iω) |
– |
некоторые |
неизвестные |
функции, |
не |
|
зависящие |
||
от t, подлежащие определению. |
|
|
|
|
|
|
|
|
|
||
|
Для нахождения W(iω) yвын (t) |
дифференцируется n раз, а x1(t) − m раз и подставляются в исходное |
|||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
дифференциальное уравнение, в результате получают |
|
|
|
|
|
|
|||||
|
|
|
|
|
AW(iω)eiωt[a (iω)n +a |
(iω)n−1 + ... +a (iω) +a ] = |
|
||||
|
|
|
|
|
|
n |
n−1 |
|
1 |
0 |
(4.15) |
|
|
|
|
|
= Aeiωt[b |
(iω)m +b |
(iω)m−1 + ... +b (iω) +b ]. |
|
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
m |
m−1 |
|
1 |
0 |
|
|
Полученное выражение (4.15) полностью совпадает с полученным ранее выражением (4.8) для АФХ и еще раз подтверждает тот факт, что амплитудно-фазовая характеристика может быть получена простой заменой переменной s на iω.
Функция W(–iω) получается аналогичным образом по формуле (4.15) заменой iω на (–iω). Записывая полученные выражения для комплексных функций W(iω) и W(–iω) в показательной фор-
ме
W (iω) = M (ω)eiϕ(ω); W (−iω) = M (ω)e−iϕ(ω) ,
частное решение уравнения (4.7) преобразуется к виду
yвын(t) = AM (ω)[eiϕ(ω)eiωt + e−iϕ(ω)e−iωt ] = 2AM (ω)cos[ωt + ϕ(ω)] .
Сравнение yвын(t), описывающего установившиеся колебания на выходе объекта, с входным сигна-
лом x(t) показывает, что отношение амплитуд выходных и входных колебаний равно |
2AM (ω) |
= M (ω) , а |
|
2A |
|||
|
|
это как раз и есть амплитудно-частотная характеристика; разность фаз [ωt + ϕ(ω)]−ωt = ϕ(ω) − фазочастот-
ная характеристика.
С изменением частоты колебаний амплитудно- и фазочастотные характеристики изменяются по определенному закону в зависимости от физических свойств объекта. Однако все реальные физические системы обладают одним общим свойством, которое заключается в том, что при увеличении частоты входных колебаний выше некоторого предела (частоты среза) ωср объект практически не реагирует на эти колебания, т.е. амплитуда выходных колебаний равна нулю. Таким образом, для любого реального
объекта lim M (ω) = 0 .
ω→∞
4.5 Физический смысл частотных характеристик
Физический смысл частотных характеристик устанавливается при их экспериментальном определении.
Пусть на вход линейного объекта подается гармонический сигнал вида x(t) = Asinωt. На выходе объекта в установившемся режиме (собственное движение прекратилось) в силу принципа суперпозиции будет наблюдаться также гармонический сигнал с частотой, равной частоте входных колебаний, сдвинутый относительно них по фазе и другой амплитуды (рис. 4.10), т.е. y(t) = Bsin(ωt + ϕ).

x(t)
A1
x
0
T1 = 2π/ω1
x(t) = A1 sin(ω1t)
|
1 |
yвых |
B |
|
0
∆t1 T1
y(t) = B1 sin(ω1t + ϕ1)
Объект |
y(t) |
а) |
|
|
б) |
|
|
2 |
в) |
|
x |
|
A |
|
|
|
|
|
|
t |
0 |
|
|
t |
|
|
|
||
|
|
|
T2 = 2π/ω2 |
|
|
|
|
x(t) = A2 sin(ω2t) |
|
г) |
yвых |
|
д) |
|
|
2 |
|||
|
|
B |
|
|
t |
0 |
|
|
t |
|
|
|||
|
|
|||
|
|
|
||
|
|
|
|
|
∆t2 T2
y(t) = B2 sin(ω2t + ϕ2)
Рис. 4.10 Экспериментальное определение частотных характеристик:
а – объект; б – входной сигнал частоты ω1; в – входной сигнал частоты ω2; г – выходной сигнал частоты ω1; д – выходной сигнал частоты ω2
Степень различия между параметрами входных и выходных гармонических сигналов не зависит от амплитуды и фазы входного сигнала, а определяется только динамическими свойствами самого объекта и частотой колебаний, поэтому в качестве динамических характеристик объекта здесь и используются рассмотренные выше частотные характеристики. Для получения последних экспериментальным путем проводится ряд опытов, для которых используется аппаратура в составе генератора гармонических колебаний с регулируемой частотой и устройства для измерения амплитуды и фазы колебаний.
В результате проведенных экспериментов частотные характеристики определяются следующим образом.
Амплитудно-частотная характеристика (АЧХ) – отношение амплитуды выходных колебаний к амплитуде входного сигнала:
|
|
M (ω) = |
B |
. |
(4.16) |
|
|
|
|||
|
|
|
A |
|
|
Фазочастотная характеристика (ФЧХ) – разность фаз выходных и входных колебаний: |
|
||||
|
|
ϕ(ω) = ϕвых – ϕвх |
(4.17) |
||
ϕ(ω) = − |
∆t(ω) |
2π , |
|
||
или |
T |
|
|
|
|
|
|
|
|
|
|
где ∆t(ω) − время сдвига.
Таким образом, амплитудно-фазовая характеристика (АФХ) может быть определена как комплексная функция, для которой АЧХ является модулем, а ФЧХ – аргументом. Последние соотношения как раз и определяют физический смысл частотных характеристик.
Имея в своем распоряжении амплитудно-фазовую характеристику, снятую экспериментально, и входной сигнал, можно записать выходной сигнал. Например, АФХ задана годографом (рис. 4.11), на вход подается сигнал x(t) = 2 sin0,5t + 3 cos0,1t – 0,8 sin10t.
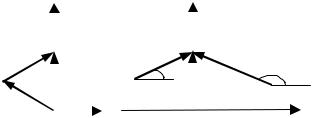
Рис. 4.11 Годограф АФХ
Выходной сигнал y(t) в рассматриваемом случае можно записать, используя принцип суперпозиции, как сумму трех сигналов
y1(t) = 2 2 sin(0,5t – π/2); y2(t) = 3 3 sin(0,1t + π/2 – π/4);
y3(t)= – 1,5 0,8 sin(10t – 3π/2);
y(t) = 4sin(0,5t – π/2) + 9 sin(0,1t – π/4) – 1,2 sin(10t – (3π/2)).
4.6 Минимально-фазовые системы
Амплитудно-фазовую характеристику системы можно записать не в виде (4.8), а, воспользовавшись теоремой Безу, как
|
m |
|
|
|
∏(iω− q j ) |
|
|
W (iω) = k |
j=1 |
, |
(4.18) |
n |
|||
|
∏(iω− s j ) |
|
|
j=1
где qj – нули, a sj − полюсы передаточной функции.
Числитель функции (4.18) представляет собой произведение сомножителей (iω – qj ). Геометрически эта разность является вектором, начало которого лежит в точке qj, а конец − на мнимой оси в точке iω (рис. 4.12). Сравнение двух векторов(iω – qj′) и (iω – qj′′), один из которых qj′ лежит в левой полуплоскости и характеризуется фазой ϕ′, а другой qj′′ – в правой полуплоскости и характеризуется фазой ϕ′′, показывает, что при одном и том же модуле всегда ϕ′ < ϕ′′, т.е. для вектора, лежащего в левой полуплоскости, фаза меньше.
Системы (звенья), все нули и полюса передаточных функций которых лежат в левой полуплоскости (действительная часть нулей и полюсов является отрицательной величиной – Re qj < 0; Re sj < 0),
называются минимально-фазовыми.
i Im(ω) |
а) |
i Im(ω) |
|
|
б) |
||
|
|||||||
i ω – q |
i ω |
|
|
|
|
i ω |
|
ϕ |
|
|
|
ϕ” |
|||
|
|
qj’ |
|
|
|
||
q |
|
’ |
|
|
|
qj” |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Re(ω) |
|
Re(ω) |
|
|
|
|
||
|
|
|
|
||||
Рис. 4.12 К определению минимально-фазовых систем
Системы (звенья), у которых хотя бы один нуль или полюс передаточной функции лежит в правой полуплоскости (действительная часть нулей, полюсов является положительной величиной – Re

qj >0;
Re sj >0), называются неминимально-фазовыми.
Можно показать, что для минимально-фазовых звеньев существуют зависимости:
|
|
|
1 |
|
∞ |
Im(ω) du; |
|
||||||
|
|
|
∫ |
|
|||||||||
Re(ω) = − |
|
|
|||||||||||
|
|
|
|
||||||||||
|
|
|
π −∞ |
u − ω |
|
|
|
||||||
|
|
|
1 |
|
∞ |
Re(ω) |
|
|
|
||||
|
|
|
|
|
|
|
|||||||
Im(ω) = − |
|
|
|
|
∫ |
|
|
|
du; |
(4.19) |
|||
|
|
|
|
u − ω |
|||||||||
|
|
|
π −∞ |
|
|
|
|||||||
|
1 |
|
∞ |
|
dL |
|
λ |
|
|
||||
|
|
|
|
|
|
||||||||
ϕ(ω) = − |
|
|
|
∫ |
|
dλ cth |
|
2 |
dλ, |
|
|||
π |
|
|
|||||||||||
|
|
|
|
−∞ |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
где L(u) = ln M(u); λ = ln ωu ; u − переменная интегрирования.
Эти зависимости показывают, что амплитудно-фазовая характеристика минимально-фазовой системы (звена) полностью определяется ее ВЧХ, МЧХ или АЧХ. Это позволяет значительно упростить задачи анализа и синтеза рассматриваемых систем, ограничиваясь изучением их ВЧХ или АЧХ.
Неминимально-фазовую систему в простейшем случае можно представить в виде последовательного соединения минимально-фазовой системы и звена, имеющего один нуль в правой полуплоскости и, соответственно, характеризующегося АФХ:
′ |
iω− q |
|
q −iω |
jπ |
. |
(4.20) |
|
W (iω) = |
|
= |
|
e |
|
||
iω+ q |
q +iω |
|
|||||
Амплитудно-частотная характеристика этого звена М ′(ω) = 1, a фазо-частотная – ϕ′(ω) = π−arctg ωq .
Таким образом, рассматриваемое звено сохраняет амплитуду выходного гармонического сигнала равной амплитуде входного сигнала при любой частоте, фаза же при изменении частоты от 0 до ∞ меняется в интервале от π до 0, т.е. включение звена с АФХ W ′(iω) приводит к добавлению положительного сдвига фазы ϕ′(ω), который при iω → 0 равен π и уменьшается при возрастании частоты.
Подобные звенья на практике используются для корректирования фазовых характеристик цепей, для повышения устойчивости и т.д.
4.7 Понятие о логарифмических частотных характеристиках
Кроме рассматриваемых выше частотных характеристик, иногда используют, так называемые, логарифмические частотные характеристики (ЛЧХ). Для их получения выражение АФХ (4.15) записывается в виде
|
b |
|
|
bm |
|
(iω)m + ... +1 |
||||
|
|
|
b |
|||||||
|
|
|
|
|
|
|
= k0M 0 (ω)eiϕ(ω) |
|||
W (iω) = |
0 |
|
0 |
|
|
|
|
|||
a0 |
|
|
(iω) |
n |
+ ... +1 |
|||||
|
|
|
|
an |
|
|
||||
|
|
|
|
|
a0 |
|
|
|
||
и логарифмируется
lgW (iω) = lgk0 +lgM0(ω) +iϕ(ω)lge .
Для оценки отношения двух величин используется логарифмическая единица – децибел. Связь между числом децибел Sдб и некоторым числом N дается формулой
Sдб = 20lg N = LmN .
Характеристика
L(ω) = Lm[k0M0(ω)] = Lmk0 + LmM0(ω) = 20lgM (ω) (4.21)
называется логарифмической амплитудной частотной характеристикой (ЛАЧХ).
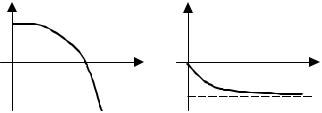
При построении логарифмических частотных характеристик по оси абсцисс откладывается частота в логарифмическом масштабе – lgω, поэтому логарифмическая амплитудная частотная характеристика строится в координатах L(ω); lgω, логарифмическая фазовая частотная характеристика (ЛФЧХ) − ϕ(ω); lgω (рис. 4.13). Логарифмические частотные характеристики называют также диаграммами Боде.
L |
а) |
ϕ |
б) |
20 lg k |
|
|
|
0 |
lgω |
0 |
lgω |
|
|
π/2 |
|
Рис. 4.13 Логарифмические частотные характеристики:
а– ЛАЧХ; б – ЛФЧХ
4.8Взаимосвязь динамических характеристик
Основной динамической характеристикой объекта или системы является дифференциальное уравнение. Кроме него могут применяться:
1)передаточная функция;
2)частотные характеристики: амплитудно-частотная, фазочастот-ная, амплитудно-фазовая;
3)переходные характеристики: переходная функция, весовая функция.
Любая из этих характеристик может быть определена, если известно дифференциальное уравнение объекта. Но, несмотря на это, следует еще раз остановиться на их взаимосвязи.
В качестве примера рассмотрим взаимосвязь между переходной функцией и другими характеристиками.
Если известна переходная функция h(t), то по формуле (3.39) определяется передаточная функция объекта W(s) = sh(s), заменой s = iω в которой, в свою очередь, могут быть получены частотные характеристики: W(iω) = (iω) h(iω).
Так как δ(t) является производной от единичной ступенчатой функции, то для линейных систем весовая функция является производной от переходной функции, т.е. w(t) = h′(t).
Дифференциальное уравнение по экспериментально снятой кривой разгона получают с помощью различных методик, позволяющих определить его коэффициенты.
Связь между основными характеристиками приведена в табл. 4.1.
При анализе динамических характеристик одним из возникающих вопросов является определение коэффициента усиления объекта, под которым понимают отношение выходной переменной к входной в установившемся режиме:
K = |
y(∞) |
, |
(4.22) |
|
A |
||||
|
|
|
но, так как y(∞) = lim y(t) , то
t→∞
lim y(t)
K = |
t→∞ |
. |
|
A |
|||
|
|
Используя теорему о конечном значении функции
lim y(t) = lim sy(s) ,
t→∞ s→0

где y(s) =W (s)X (s) = W (ss)A , можно записать, что
lim y(t) = lim |
sW (s)A |
= AlimW (s) . |
||
s |
||||
t→∞ |
s→0 |
s→0 |
||
При единичном ступенчатом воздействии А = 1 и тогда
lim y(t) = limW (s) = b0 . |
||
t→∞ |
s→0 |
a0 |
4.9 Тренировочные задания

1 Основной частотной характеристикой является амплитудно-фазовая характеристика (АФХ), которой называется конформное отображение мнимой оси плоскости корней характеристического уравнения на плоскость АФХ. Амплитудно-фазовая характеристика является комплексной функцией и может быть записана в показательной форме
W (i ω) = M (ω)ei ϕ(ω)
и алгебраической форме
W (i ω) = Re(ω) + i Im(ω),
где М(ω) называется амплитудно-частотной характеристикой (АЧХ); ϕ(ω) – фазочастотной характеристикой (ФЧХ); Re(ω) – вещественно-частотной характеристикой (ВЧХ); Im(ω) – мнимой частотной характеристикой (МЧХ). Между этими характеристиками существует связь.
А Сформулируйте основные свойства конформного отображения.
В Если известны АЧХ и ФЧХ, то каким образом определяются ВЧХ и МЧХ? С Как перейти от ВЧХ и МЧХ к АЧХ и ФЧХ?
2 Частотные характеристики могут быть получены экспериментально в результате подачи на вход объекта гармонического сигнала, а также теоретически в передаточной функции комплексного параметра s на iω.
А Какие частотные характеристики получают экспериментально?
ВЗадана передаточная функция W (s) = s +3 4 , запишите амплитудно-фазовую характеристику в показательной и алгебраической форме.
СЗадано дифференциальное уравнение объекта управления y′′(t) + 4y′(t) + 4y(t) = 3x(t) , запишите ам- плитудно-фазовую характеристику.
3 Амплитудно-фазовая характеристика связана с другими динамическими характеристиками.
А Как определить весовую функцию по амплитудно-фазовой характеристике? В Как определить АФХ по переходной функции?
СЗадана весовая функция w(t) = e−t , запишите АФХ.
4.10Тест
1 В соответствии со свойствами конформного отображения линия переходит…
А В линию. В В точку.
С В треугольник.
2 Амплитудно-фазовая характеристика является…
А Случайной функцией. В Комплексной функцией.
С Детерминированной функцией.
3 Как экспериментально получают частотные характеристики? Подачей на вход объекта…
А Гармонического сигнала x(t) = Asinωt . В δ-функции – x(t) = δ(t) .
С Единичного ступенчатого сигнала x(t) =1(t) .
4 Как перейти от передаточной функции к частотным характеристикам? Положив…
