ЛЕКЦИЯ_1 / Основы теории автоматического управления - УП - Лазарева-Мартемьянов - 2004 - 352

Рис. 3.5 Иллюстрация эксперимента по проверке объекта

Рис. 3.6 Линеаризация нелинейной статической характеристики

Одним из наиболее распространенных способов линеаризации является разложение нелинейной функции в ряд Тейлора в окрестности заданной точки и исключение нелинейных членов разложения.

Пусть статическая характеристика описывается нелинейной n раз дифференцируемой, где n – любое натуральное число, функцией у = f (x), которую необходимо линеаризовать в окрестности точки (x0, y0) (рис. 3.6).

Если в пределах максимально возможных отклонений у и x от x0 и у0 f (x) мало отличается от линейной функции, то можно f (x) заменить ее приближением y = f (x) . Функция f (х) находится из ряда

Тейлора:

Под системой в дальнейшем будет пониматься любое множество элементов (может быть отдельный элемент), образующее некоторое целостное единство безотносительно к функциям, которые они выполняют, т.е. это может быть объект, регулятор, система регулирования и т.д.

Система называется динамической, если она описывается дифференциальными, интегральными либо конечными уравнениями, завися-

Основной задачей изучения динамического поведения линейной системы является получение возможности рассчитывать выходной сигнал y(t) для любого известного входного сигнала x(t). В связи с этим необходимо располагать математическим аппаратом для исследования линейной системы (рис. 3.8).

Основными динамическими характеристиками, используемыми в теории автоматического управления, являются передаточная функция, дифференциальное уравнение, временные характеристики: переходная функция, весовая функция; частотные характеристики: амплитудно-фазовая характеристика

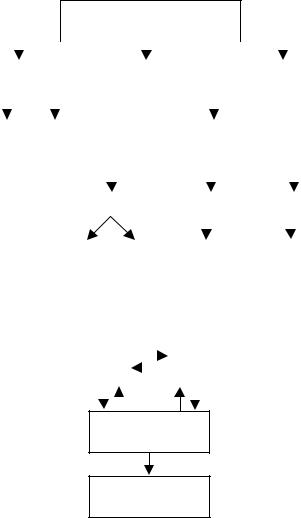
(АФХ), расширенная амплитудно-фазовая характеристика (РАФХ), логарифмические частотные характеристики (ЛАФХ). Составляющими основных частотных характеристик являются

Динамические

характеристики

Передаточная

функция

Частотные

характеристики

Рис. 3.9 Взаимосвязь динамических характеристик

амплитудно-частотная характеристика (АЧХ), фазо-частотная характеристика (ФЧХ), вещественночастотная характеристика (ВЧХ), мнимая частотная характеристика (МЧХ) и соответственно расширенные – РАЧХ, РФЧХ и логарифмические – ЛАЧХ, ЛВЧХ.

Между этими характеристиками существует связь, которую иллюстрирует схема, изображенная на рис. 3.9.

Ряд динамических характеристик можно получить экспериментальным путем, а некоторые являются теоретическими. На практике экспериментально получают временные характеристики и частотные, точнее, АЧХ и ФЧХ, и уже на основе их записываются дифференциальное уравнение, передаточная функция, а также расширенные и логарифмические частотные характеристики. Таким образом, чтобы оценить динамическое поведение линейной системы, необходимо познакомиться со всеми динамическими характеристиками.

3.5 Динамические процессы в системах

Основным математическим аппаратом при изучении и исследовании систем управления является аппарат дифференциальных уравнений. Круг рассматриваемых объектов был уже определен – это линейные объекты с сосредоточенными координатами. При этом различают стационарные объекты, коэффициенты дифференциальных уравнений которых не изменяются во времени, и нестационарные объекты, у которых коэффициенты изменяются с течением времени, например, изменение теплопроводности, старение катализатора и др.

Большинство объектов регулирования являются нестационарными объектами, однако, скорость изменения их свойств намного меньше скорости регулирования, поэтому такие объекты при расчете систем регулирования можно приближенно рассматривать как стационарные в течение определенного промежутка времени, за который свойства объекта не успевают существенно измениться.

Далее будут рассматриваться линейные стационарные объекты (системы) с сосредоточенными координатами, которые описываются обыкновенными дифференциальными уравнениями с постоянными коэффициентами:

an y(n) (t) + an−1y(n−1) (t) +...+ a1y′(t) + a0 y(t) = bm x(m) (t) +bm−1x(m−1) (t) +...

Уравнение (3.8) описывает поведение объекта, который имеет статическую характеристику y = b0 x a0

в неустановившемся (переходном) режиме при любой форме входного сигнала x(t). Частными случаями уравнения (3.8) являются уравнения

an y(n) (t) + an−1y(n−1) (t) +...+ a1y′(t) + a0 y(t) = bm x(m)(t) +bm−1x(m−1) (t) +...

an y(n) (t) + an−1y(n−1) (t) +...+ a1y′(t) = bm x(m) (t) +bm−1x(m−1) (t) +...

Для объектов, описываемых уравнением (3.8, а), статическая характеристика существует, но является вырожденной, так как b0 = 0. Для объектов же, описываемых уравнением (3.8, б), статическая характеристика не существует.

Объекты, имеющие статическую характеристику, называются статическими, а не имеющие статической характеристики, называются астатическими.

В большинстве случаев, как уже отмечалось выше, уравнения систем автоматического регулирования оказываются нелинейными, поэтому, если это возможно, проводят линеаризацию этих уравнений при помощи ряда Тейлора путем разложения нелинейных функций некоторых переменных по степеням малых приращений этих переменных, взятых в окрестности их значений, соответствующих установившемуся режиму. В результате получают линеаризованные уравнения в отклонениях. Таким образом, в большинстве случаев дифференциальное уравнение (3.8) является уравнением в отклонениях, которое описывает объект или систему регулирования только в окрестности установившегося режима. Для линейных систем уравнения в отклонениях и исходные уравнения совпадают.

Для получения решения уравнения (3.8) необходимо задать начальные условия, под которыми понимается состояние процесса в момент времени, принятом за его начало t = 0:

Общее решение уравнения (3.8) представляется в виде:

В выражении (3.10) yсв(t) является общим решением соответствующего однородного уравнения и увын(t) – частное решение неоднородного уравнения (3.8). Следовательно, yсв(t) соответствует движению системы в отсутствии входного сигнала x(t) ≡ 0, т.е. собственному свободному движению системы, и определяется свойствами самой системы, которые проявляются в свойствах корней характеристического уравнения. Если эти корни различны, то

i=1

где λi – корни характеристического уравнения; сi – произвольные постоянные, определяемые из на-

чальных условий.

Частное решение увын(t) зависит от вида функции x(t), определяющей входное воздействие на систему, и соответствует вынужденному движению (состоянию) системы.

Решение (3.10) уравнения (3.8) определяет динамический процесс в системе, происходящий с момента подачи входного воздействия, который принят за начало отсчета времени, поэтому движение системы (переходной процесс) рассматривается только при t ≥ 0 , для t < 0 он принят тождественно равным нулю.

Выходной сигнал y(t), получающийся в течение такого процесса, является наиболее полной характеристикой динамических свойств системы, поэтому определение этого сигнала, как уже отмечалось, и является основной задачей теории регулирования. Здесь становится актуальной идея изучения динамических свойств системы с помощью временных характеристик.

3.6Переходная и весовая функции

3.6.1ПЕРЕХОДНАЯ ФУНКЦИЯ

Для получения переходной функции в качестве стандартного сигнала используется единичная функция времени (2.16). Такого рода воздействию соответствует, например, сброс или включение нагрузки в системах регулирования (отказ мотора в системе регулирования).

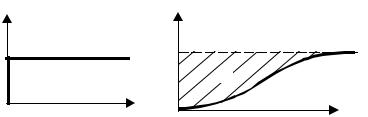
Рис. 3.10 Переходная характеристика химического реактора:

а – ступенчатое воздействие; б – кривая разгона

Переходной функцией называется аналитическое выражение для решения линейного дифференциального уравнения (3.8) при входном сигнале x(t) = 1(t) и нулевых начальных условиях, т.е.

an y(n) (t) + an−1y(n−1) (t) +...+ a1y′(t) + a0 y(t) = b01(t),

Кривой разгона называется реакция объекта (системы) на единичное ступенчатое воздействие при нулевых начальных условиях.

На практике кривая разгона определяется экспериментальным путем и используется в качестве исходных данных для анализа и синтеза систем автоматического управления исследуемом объектом.

Здесь следует ввести понятия прямой и обратной задач. Прямая задача (задача Коши) заключается в определении решения дифференциального уравнения с заданными начальными условиями. В обратной задаче требуется восстановить вид и коэффициенты дифференциального уравнения по известной интегральной кривой, например, переходной функции. Решение обратной задачи представляет значительную сложность вследствие ее некорректности и здесь существует специальный математический аппарат. Так, например, если предположить, что переходная функция описывается решением уравнения первого порядка

a1y′(t) + a0 y(t) = b0x(t) , x(t) = 1(t), у(0) = 0, или Ty′(t) + y(t) = kx(t),

Если для представления входного сигнала использовать не формулу (2.26), а (2.27), то интеграл Дюамеля записывается через переходную функцию:

3.8 Преобразование Лапласа

Основным математическим аппаратом, который используется в теории автоматического управления, является специальный метод прикладного анализа, так называемый операционный метод, в основе которого лежит функциональное преобразование Лапласа.

3.8.1 ОПРЕДЕЛЕНИЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА

Преобразованием Лапласа называется преобразование функции x(t) переменной t в функцию х(s) другой переменной s при помощи оператора, определяемого соотношением

Формула (3.16) определяет прямое преобразование Лапласа. Возможно и так называемое обратное преобразование Лапласа, позволяющее по изображению найти оригинал. Оно определяется соотношением

где с – абсцисса сходимости функции x(s).

Для большинства функций, встречающихся на практике, составлены таблицы соответствия между оригиналами и изображениями. Изображения некоторых наиболее часто встречающихся функций в теории управления приведены в табл. 3.1. Если же функция отсутствует в таблице, то ее изображение можно получить непосредственно, пользуясь соотношением (3.16).

Пример 3.1 Требуется найти преобразование Лапласа от функции x(t) = е–at. Согласно определению преобразования Лапласа (3.16) имеем

Таким образом, e−at → s +1 a .