
ЛЕКЦИЯ_1 / Основы теории автоматического управления - УП - Лазарева-Мартемьянов - 2004 - 352
.pdf
2.7 Представление сигналов
Сигналы могут быть представлены различным образом, при этом входной сигнал всегда является непрерывным, а представлению подлежит сигнал на выходе.
Один и тот же сигнал может иметь различную физическую природу – электрическую, звуковую, световую и т.д.
В теории управления наибольшее распространение получило математическое представление сигналов. Все виды математических представлений сигналов делятся на три основные группы:
1)непрерывное представление – выходной сигнал определен в любой момент времени (рис. 2.4, б);
2)дискретно-непрерывное представление – выходной сигнал является квантованным по времени и
непрерывно изменяется только по уровню (рис. 2.4, в); 3) дискретное представление – выходной сигнал квантован как по времени, так и по уровню (рис.
2.4, г).
|
x(t) |
Объект |
y(t) а) |
|
|
|
|
|
|
|
|
|
|
y |
б) |
y |
|
в) |
y |
г) |
0 |
t |
0 |
|
t |
0 |
t |
Рис. 2.4 Виды математических представлений сигналов:
а– блок-схема системы; б – непрерывное; в – дискретно-непрерывное;
г– дискретное
Врезультате квантования сигнала по времени при дискретно-непрерывном и дискретном представлениях может произойти потеря информации, так как остаются значения сигнала только в дискретные моменты времени. Однако благодаря одному из свойств реальных систем в них при определенных условиях сохраняется полная информация о сигнале, если последний известен лишь в дискретные моменты времени. Это свойство известно как теорема Котельникова: сигнал, описываемый функцией с ограниченным спектром, полностью определяется своими значениями, отсчитанными через интервал вре-
мени ∆t = 12 Fс , где Fc – ширина спектра сигнала.
Смысл теоремы Котельникова состоит в том, что, если требуется передавать сигнал, описываемый функцией f (t) с ограниченным спектром, то достаточно передавать отдельные мгновенные значения, отсчи-
танные через конечный промежуток времени ∆t = 12 Fс . По этим значениям непрерывный сигнал может быть
полностьювосстановлен на выходе системы.
Математические представления сигналов на практике чаще всего реализуются в виде модуляции. Под модуляцией понимают изменение одного из параметров какого-либо физического процесса по закону представляемого сообщения. Так, в системах с электрическими сигналами под модуляцией понимают изменение одного из параметров высокочастотного электрического сигнала по закону передаваемого низкочастотного сообщения. В случае модуляции гармонического сигнала различают два основных вида модуляции: амплитудная модуляция и угловая модуляция, которая подразделяется на частотную и фазовую. На практике чаще всего встречаются смешанные виды модуляции – амплитуднофазовая или амплитудно-частотная, при этом один из видов модуляции является полезным, другой – паразитным.
2.8 Сигналы. Их виды
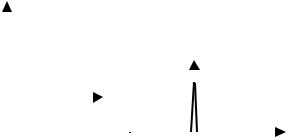
Наиболее часто в теории автоматического управления используются следующие сигналы. 1 Единичный скачок (рис. 2.5):
0 |
при t < 0; |
(2.16) |
x(t) =1(t) = |
при t ≥ 0. |
|
1 |
|
1(t) называется также функцией Хевисайда. Строго говоря, функция Хевисайда физически нереализуема, однако, если, к примеру, на исследуемом объекте резко открыть вентиль, в результате чего расход
x |
|
|
|
|||
1 |
|
|
|
x |
||
|
|
|
||||
|
|
|
|
|||
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
Рис. 2.5 Единичный |
|
|
t |
|||
|
|
|||||
скачок |
|
|
||||
|
|
|
||||
Рис. 2.6 Единичный импульс
подаваемого вещества изменится скачком с F1 до F2 , то говорят, что на входе объекта реализован скачкообразный сигнал величиной F2 – F1 , и если последняя разность равна единице, то на входе реализуется единичный скачок.
Спектральная характеристика для единичного скачка:
|
1 |
−i |
π |
|
|
|
2 . |
||||
F(iω) = |
|
e |
|||
ω |
|||||
|
|
|
|
||
2 Единичная импульсная функция – дельта-функция (рис. 2.6) – это функция, удовлетворяющая следующим условиям:
1) |
0 |
приt ≠ 0; |
δ(t) = |
|
|
|
∞ приt = 0; |
|
|
∞ |
(2.17) |
2) |
∫δ(t)dt =1. |
|
−∞
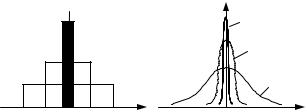
Дельта-функцию называют также функцией Дирака, она относится к классу сингулярных функций. Эту физически также нереализуемую функцию можно представить как импульс бесконечно малой длительности и бесконечно большой амплитуды, т.е. как предел, к которому стремится прямоугольный импульс с основанием ∆t и площадью, равной единице (рис. 2.7, а), если ∆t → 0 так, чтобы площадь импульса сохранялась равной единице. Также δ-функцию можно представить как предел некоторой функ-
ции (рис. 2.7, б):
δ(t) = limδ(t,β) = lim |
β |
|
. |
(2.18) |
|
|
+1) |
||||
β→∞ |
β→∞ π(β2t2 |
|
|
||
К основным свойствам дельта-функции можно отнести следующие равенства:
0+
∫δ(t)dt =1;
0−
x
0
|
(2.19) |
|
а) |
x |
б) |
|
|
β = 10 |
|
|
β = 5 |
|
|
β = 1 |
t |
0 |
t |
Рис. 2.7 Представление дельта-функции:
а – прямоугольный импульс; б – δ(β, t)-функция
δ-функция является четной функцией:
δ(t) = δ(–t); |
(2.20) |
∞ |
|
∫x(t)δ(t)dt = x(0) , |
(2.21) |
−∞
т.е. из непрерывной функции можно "вырезать" одну ординату.
Последнее соотношение, используя рассмотренные уже свойства δ-функции, доказывается следующим образом:
∞ 0− 0+ ∞ 0+
∫x(t)δ(t)dt = ∫x(t)δ(t)dt + ∫x(t)δ(t)dt + ∫x(t)δ(t)dt = x(0) ∫δ(t)dt = x(0).
−∞ −∞ 0− 0+ 0−
Спектральная характеристика дельта-функции: F(iω) = 1.
Между функцией Хевисайда и функцией Дирака существует связь, выражаемая соотношением:
τ |
(2.22) |
∫δ(t)dt =1(τ), или δ(t) =1[t] . |
|
′ |
|
−∞
На практике считается, что на вход объекта подана δ-функция, если время действия прямоугольного импульса намного меньше времени переходного процесса.
3 Гармонический сигнал (рис. 2.8, а) |
|
x(t) = A sinωt |
(2.23) |
используется при исследовании систем автоматического регулирования частотными методами. Синусоидальный гармонический сигнал можно представить как вращение вектора длиной А вокруг
начала координат (рис. 2.8, б) с некоторой угловой скоростью ω, рад/с.
Гармонический сигнал характеризуется такими параметрами, как амплитуда – А; период – Т; фаза –
ϕ.

x |
|
|
а) |
x |
|
б) |
|
|
b |
T |
|
b |
|
|
|
|
|
|
||
|
|
A |
c |
c |
ϕ |
a |
|
a |
|
||||
|
|
t |
|
|
t |
|
|
|
|
|
|
||
|
|
|
d |
|
|
|
|
|
|
|
|
d |
|
|
|
|
x |
в) |
|
|
t
∆t
Рис. 2.8 Гармонический сигнал:
а – обычный сигнал; б – представление гармонического сигнала вращением вектора; в – гармонический сигнал со сдвигом фазы
Между периодом и угловой скоростью справедливы соотношения
ω = |
2π |
и |
T = |
2π |
. |
(2.24) |
T |
|
|||||
|
|
|
ω |
|
||
Если колебания начинаются не из нуля, то они характеризуются фазой колебаний (рис. 2.8, в), которая во временной области характеризуется отрезком ∆t, но обычно фазу выражают в радианах – ϕ (рис. 2.8, б). Перевод осуществляется по формуле
ϕ |
= |
2π∆t |
. |
(2.25) |
|
||||
|
|
T |
|
|
На практике для получения гармонического сигнала используется генератор синусоидальных колебаний.
4 Сдвинутые элементарные функции.
К этим функциям относятся функции Хевисайда и Дирака с запаздыванием, т.е. 1(t – τ) и δ(t – τ) (рис. 2.9),
0, t ≠ τ;
причем δ(t − τ) = ∞ =, t τ.
Все свойства δ-функции сохраняются, но записываются в виде:
x |
|
|
а) |
x |
|
б) |
|||
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
0 |
τ |
|
t |
0 |
τ |
|||
Рис. 2.9 Сдвинутые элементарные функции
x |
|
а) |
x |
|
|
б) |
~ |
|
в) |
|
|
|
|
|
x |
|
|
||
|
|
|
|
|
|
(t) |
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
∆ti |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
ti |
t |
0 |
|
τ |
t |
|
0 |
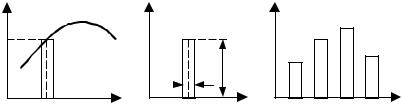
t Рис. 2.10 Сигнал произвольной формы: |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
а – входной непрерывный сигнал; б – импульс x(i); |
||||
|
|
|
|
в – суперпозиция импульсов, определяющих сигнал x(t) |
|||||
τ+
∫δ(t − τ)dt =1;
τ−
δ(t − τ) = δ(τ−t) = δ(−(t − τ));
∞
∫x(t) δ(t − τ) dt = x(τ).
−∞
5 Сигнал произвольной формы – x(t) (рис. 2.10, а).
Любой сигнал произвольной формы можно представить с помощью δ-функции. С этой целью выделяется произвольный момент времени t, и строится столбик высотой x(t) (рис. 2.10, б), соответствующий значению сигнала в момент времени t = ti, и основанием ∆ti.
Этот импульс можно выразить через приближенную дельта-функцию – ~δ (t – ti):
|
|
|
|
~ |
площадь равна1; |
||
|
|
|
|
δ(t - ti ) = ширина равна ∆ti ; |
|||
|
|
1 |
|
|
высота равна |
, |
|
|
|
||
|
|
∆ti |
|
т.е. |
~ |
|
|
|
|
|
xi (t) = x(ti )∆ti δ(t −ti ) . |
|
|
|
|
||
|
Заменяя функцию x(t) набором импульсов (рис. 2.10, в), можно записать: |
~ |
n |
~ |
||
|
|
|||||
|
x(t) = ∑x(ti )∆ti δ(t −ti ) . |
|||||
|
|
~ |
|
|
i=1 |
|
|
Если теперь |
|
|
|
|
|
|
n → ∞, ∆ti → dτ,δ(t − ti ) → δ(t − τ) , то |
|
|
|
|
|
|
|
t+ |
|
|
|
|
|
|
x(t) = ∫x(τ)δ(t −τ)dτ. |
(2.26) |
|
|
|
0
Сигнал произвольной формы можно представить и через единичные функции, для чего выражение (2.26) следует проинтегрировать по частям, используя соотношениеδ(t − τ) =1′(t − τ) , в результате чего получают следующее соотношение
t + |
|
x(t) = x(0) 1[t]+ ∫x′(τ) 1(t − τ)dτ . |
(2.27) |
0 |
|
2.9Тренировочные задания
1В системах автоматического управления наблюдаются различные воздействия и сигналы. Для упрощения анализа и синтеза конкретных систем пользуются разработанной типизацией этих воздействий и сигналов.
АКакой сигнал называется регулярным?
В Какие существуют виды представления сигналов?
С Какие сигналы относятся к основным типам регулярных сигналов?
2 Для характеристики спектров сигналов используется преобразование Фурье. Спектр периодических сигналов характеризуется определенными свойствами. Для непериодического сигнала вводится понятие спектральной плотности.

А Какое преобразование называется преобразованием Фурье?
В Какими характерными свойствами обладает спектр периодического сигнала? С Что такое спектральная характеристика непериодической функции?
3 В теорииавтоматическогоуправленияиспользуются такназываемые стандартные сигналы, ккоторым относятся единичный скачок, единичная импульсная функция – дельта-функция, гармонический сигнал.
А Какая функция называется дельта-функцией?
B Как на исследуемом объекте подать сигнал в виде единичного скачка?
СКакимипараметрами характеризуется гармонический сигнал?
2.10Тест
1 Сигнал называется регулярным, если его математическим представлением является:
А Заранее заданная функция времени. В Заранее заданная функция частоты.
С Заранее заданная функция времени и частоты.
2 Сигнал называется периодическим, если он представляет собой:
А Функцию времени и удовлетворяет условию
f(t) = f(t + T) , −∞ ≤ t ≤ ∞.
В Функцию времени и удовлетворяет условию
f(t) = f(t + T), t1 ≤ t ≤ t2.
С Функцию частоты и удовлетворяет условию
f(ω) = f(ω + W), −∞ ≤ ω ≤ ∞.
3 Какое из преобразований называется преобразованием Фурье?
∞
А F(i ω)= ∫ f (t)eiωt dt .
−∞
∞
В F(ω)= ∫ f (t)e−iωt dt .
−∞
∞
С F(i ω)= ∫ f (t)e−iωt dt .
−∞
4 Спектральной плотностью непериодического сигнала называется величина
А F(iω)= π1 ddAω .
В F(iω)= π1 ddAω .
С F(iω)= π ddAω ,
где А– бесконечно малые амплитуды непериодической функции.
5 Функцией Хевисайда называется функция:
0 приt < 0;
А x(t) =
1 приt ≥ 0. В x(t) =1 при t.
С x(t) = 0 при0>t > t2;1 при0≤ t ≤ t1.
6 Дельта-функцией называется функция, удовлетворяющая условиям:
∞ при t = 0;
А δ(t) =
0 при t ≠ 0.
0 при t ≠ 0;
В δ(t) =
∞ при t = 0;
0 при t ≠ 0;
С δ(t) =
∞ при t = 0;
∞
∫δ(t)dt =1 .
−∞
∞
∫δ(t)dt = 0 .
−∞
7 Какая функция относится ксдвинутым элементарным функциям?
А x(t).
В x(t – τ).
С x(t) + x(τ).
8 Сигнал произвольной формы можно представить как:
t
А x(t) = ∫x(τ)h(t − τ)dτ.
0
t
В x(t) = ∫x(τ)δ(t − τ)dτ .
0
t
С x(t) = ∫x(τ)h(t − τ)δ(τ)dτ .
0
9 Сигнал называется гармоническим, если
А x(t) = Ah(t)sinωt .
В x(t) = Aδ(t)sinωt .
С x(t) = Asinωt .
10Между функцией Хевисайда и функцией Дирака существует связь, выражаемая соотношением
А1[t] = δ' (t).
В δ(t) = 1' [t].
∞
С ∫1[t]dt = δ(t) .
0
3 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ
АВТОМАТИЧЕСКИХ СИСТЕМ
3.1 Основные способы математического описания. Уравнения движения
Математическое описание автоматической системы управления – это описание процессов, протекающих в системе на языке математики.
Построение любое системы управления начинается с изучения объекта управления и составления его математического описания.
В качестве объекта может выступать аппарат, технологический процесс, производство, предприятие и отрасль. Различие математических моделей объектов обуславливается их назначением. Эти модели описывают различные режимы работы объекта или системы управления и могут быть получены одним из способов: экспериментальным, аналитическим, комбинированным или экспериментальноаналитическим.
При экспериментальном способе уравнения моделей получают путем постановки специальных экспериментов (метод активного эксперимента) или путем статистической обработки результатов длительной регистрации переменных объекта в условиях его нормальной эксплуатации (метод пассивного эксперимента).
При аналитическом описании уравнения моделей получают на основании физико-химических закономерностей протекающих процессов.
При экспериментально-аналитическом подходе уравнения моделей получают аналитическим путем с последующим уточнением параметров этих уравнений экспериментальными методами.
При разработке математического описания автоматических систем следует учитывать основные методологические положения теории автоматического управления. Это прежде всего системный подход к решению задач управления, рассматривающий поведение объекта и регулятора в процессе регулирования в неразрывной взаимосвязи; возможность применения методов теории автоматического управления к системам самой разнообразной физической природы вследствие абстрагирования математических моделей от конкретных физических систем. Кроме того, система рассматривается как цепь взаимодействующих физически и информационно элементов и обладает способностью передавать физические воздействия и информационные сигналы в одном, строго определенном направлении; каждый же элемент системы рассматривается как преобразователь входного воздействия в выходную реакцию. Математическое описание как отдельных элементов, так и системы в целом составляется, как правило, с рядом допущений и упрощений, удачность которых зависит от глубины знаний исследователя системы в данной области, его интуиции и обязательно подлежит экспериментальной проверке.
Вобщем случае уравнения математической модели объекта или системы управления, устанавливающие взаимосвязь между входными и выходными переменными, называются уравнениями движения.
Уравнения, описывающие поведение системы регулирования в установившемся режиме при постоянных воздействиях, называются уравнениями статики.
Уравнения, описывающие поведение системы регулирования при неустановившемся режиме при произвольных входных воздействиях, называются уравнениями динамики.
Все объекты регулирования можно разделить на два класса: объекты с сосредоточенными координатами, динамика которых описывается обыкновенными дифференциальными уравнениями, и объекты
сраспределенными координатами, динамика которых описывается дифференциальными уравнениями в частных производных. В дальнейшем рассматриваются только объекты с сосредоточенными координатами.
Вкачестве примера можно рассмотреть объект с сосредоточенными координатами, описываемый дифференциальным уравнением второго порядка (рис. 1.2)
F(y, y , y , x, x ) + f = 0 , |
(3.1) |
|
|
|
|
|||
′ |
′′ |
′ |
|
|
|
|
|
|
где y – выходная переменная; x, f – входные переменные; |
y , x |
′ |
– первые производные по времени; y |
′′ |
– |
|||
|
|
|
|
′ |
|
|
||
вторая производная по времени.
При постоянных входных воздействиях x = x0; f = f0 с течением времени выходная величина принимает постоянное значение y = y0 и уравнение (3.1) преобразуется к виду:
F(y0, 0, 0, x0, 0) + f0 = 0 . |
(3.2) |
Конечное уравнение (3.2) является уравнением статики.
Статический режим можно характеризовать с помощью статических характеристик. Статической характеристикой объекта (системы) называется зависимость выходной величины от
входной в статическом режиме.
Статическую характеристику можно построить экспериментально, если подавать на вход объекта постоянные воздействия и замерять выходную переменную после окончания переходного процесса. Если объект имеет несколько входов, то он характеризуется семейством статических характеристик. В свою очередь, сама статическая характеристика характеризуется коэффициентом k, который определя-
ется как k = dy |
. Для объектов с нелинейной статической характеристикой коэффициент усиления явля- |
||||
dx |
|
|
|
|
|
ется переменной величиной, для объектов же с линейными статическими характеристиками коэффици- |
|||||
ент усиления – величина постоянная (рис. 3.1). |
|
|
|
||
|
а) |
|
б) |
|
|
|
y |
α = arctg k |
y |
|
x |
|
|
|
|
||
|
|
α |
∆y |
|
k = ∆y ⁄∆x |
|
|
|
|
||
|
|
|
|
|
|
|
0 |
x |
0 |
∆x |
x |
Рис. 3.1 Статическая характеристика объектов:
а– нелинейного; б – линейного
3.2Примеры уравнений объектов управления
Втеории автоматического управления широко используется метод математических аналогий, согласно которому различные по физической природе объекты описываются однотипными математическими зависимостями.
Рассмотрим некоторые примеры составления уравнений статики и динамики для различных по физической природе объектов.
3.2.1 ГИДРАВЛИЧЕСКИЙ РЕЗЕРВУАР
Примером простейшего объекта автоматического управления является гидравлический резервуар, в котором имеется приток и сток жидкости. Принципиальная и структурная схемы представлены на рис. 3.2.
Основной координатой, характеризующей состояние рассматриваемого объекта, является уровень жидкости Н, который выбирается в качестве выходной регулируемой величины. Входным и соответственно регулирующим воздействием является скорость притока воды в резервуар Q, внешним возмущением – расход воды из резервуара G. При постоянной степени открытия дросселя на притоке жидкости, уровень
Q |
а) |
|
|
|
(xв) |
|
G |
|
б) |
|
|
|
Q |
|
|
|
H |
||
|
|
|
|
|
|||||
|
|
|
|
||||||
|
|
|
|
|
|
|
|||
|
H |
Объект |
|||||||
|
(x) |
|
(y) |
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
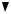 G
G
Рис. 3.2 Гидравлическая емкость:
а – принципиальная схема; б – структурная схема
определяется разностью (Q – G). По условиям работы объекта величина притока Q изменяется произвольно во времени.
Уравнение динамики, описывающее зависимость уровня H в переходном режиме от Q, в соответствии с законом гидравлики записывается в виде
S |
dH |
= Q −G , |
(3.3) |
|
dt |
||||
|
|
|
где S – площадь поперечного сечения резервуара.
Уравнение (3.3) представляет собой математическое описание объекта регулирования – гидравлической емкости и является обыкновенным дифференциальным уравнением 1-го порядка.
3.2.2 ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ
Электрической емкостью называется цепь, состоящая из сопротивления R и емкости С (рис. 3.3).
|
|
R |
|
а) |
|
|
б) |
|||
|
|
|
|
|
|
|
Uвх |
|
q |
|
Uвх |
|
|
|
|
С |
Объект |
||||
|
||||||||||
|
|
|
|
|
|
|||||
|
|
|
|
(x) |
(y) |
|||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
Рис. 3.3 Электрическая емкость:
а – принципиальная схема; б – структурная схема
Выходной координатой такого объекта может быть выбран заряд q на обкладках конденсатора, а входной – напряжение на входе цепи Uвх.
Дифференциальное уравнение может быть получено на основе закона Кирхгофа:
R |
dq |
+ |
q |
=Uвх . |
(3.4) |
|
dt |
C |
|||||
|
|
|
|
Таким образом, математическим описанием электрической емкости является обыкновенное дифференциальное уравнение 1-го порядка.
3.2.3 ХИМИЧЕСКИЙ РЕАКТОР ПОЛНОГО ПЕРЕМЕШИВАНИЯ
Пусть в реакторе протекает химическая реакция типа А → B (рис. 3.4). При выводе уравнений приняты следующие допущения:
1)в реакторе осуществляется идеальное перемешивание реакционной смеси, т.е. концентрация во всех точках реактора одинакова;
2)теплоемкость реакционной смеси постоянна и равна теплоемкости исходного реагента;
3)реакция протекает в изотермических условиях, т.е. температура в реакторе постоянна.
A |
а) |
|
|
|
б) |
|
|
|
|
||
CA |
|
CA |
|
C |
|
B |
|
A |
|||
0 |
0 |
Объект |
|
||
|
(x) |
(y) |
|||
|
CA |
|
|
|
|
Рис. 3.4 Химический реактор:
а – принципиальная схема; б – структурная схема
При этих допущениях реактор может рассматриваться как объект с сосредоточенными параметрами, материальный баланс которого имеет следующий вид:
Измене- |
Количество |
Количе- |
Количе- |
ние ко- |
реагента А, |
ство вы- |
ство ве- |
личества |
= поступивше- |
– шедшего |
– щества А, . |
вещества |
го |
вещества |
вступивш |
А |
в реактор во |
А |
его в |
