Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Керченский государственный морской технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ЛЕКЦИЯ_1 / Основы теории автоматического управления - УП - Лазарева-Мартемьянов - 2004 - 352

.pdf

Скачиваний:

Добавлен:

08.02.2016

Размер:

2.64 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 2223 / 2623 24 25 26 > Следующая >>>

)

daij (yi )

= ∑

yi2

2aii (yi )

+ 2∑

j =2

i =1

(12.38)

j ≠i

dy j

× y

+ a

)

Работу метода Г. Сеге удобнее проследить на примере систем второго порядка. В этом случае (12.37) примет вид

V = a11(y1)y12 + 2a12 (y1)y1y2 + a22 (y2 )y22 .	(12.39)
Определению подлежат коэффициенты a11(y1) ,	a12 (y1) , a22 (y2 ) . Принимается, что a22 (y2 ) =1, тогда

V = a11(y1)y12 + 2a12 (y1)y1 y2 + y22 ,

и, следовательно, производная (12.38) записывается следующим образом

= da11(y1) y2 dy1

+ 2a

) dy1 + 2 da12 (y1)

y y

dy1

(12.40)

)

dy1

+ 2a

(y )y

dy2

+ 2y

dy2

2 dt

Так как исходная нелинейная система второго порядка записывается в виде

dy1(t)dtdy2 (t)dt

=F1(y1, y2 ); ,

=F2 (y1, y2 ),

то производная от функции Ляпунова в силу этих дифференциальных уравнений будет


dV	=		da11(y1)		y2F (y , y					2	) + 2a (y )y F (y , y					2	) +
	=				y2F (y , y						) + 2a (y )y F (y , y						) +
dt			dy1			1	1	1			11	1	1	1	1
dt			dy1
+ 2		da12 (y1)		y y		2	F (y , y		2		) + 2a	(y )y F (y , y				2	) + (12.41, а)
+ 2				y y			F (y , y				) + 2a	(y )y F (y , y					) + (12.41, а)
	1						1	1			12	1	1	2	1
			dy1

+ 2a12 (y1)F1(y1, y2 )y2 + 2y2 (y1, y2 ).

Предположим, что правая часть производной функции Ляпунова представляет собой полином второго порядка относительно yk

	ψ(y1,y2 ) = A2 (y1)y22 + A1(y1)y2 + A0 (y1) ,	(12.41, б)
где A0 , A1, A2	– полиномы, зависящие от y1 .
Для обеспечения устойчивости во всей области (y1, y2 )			необходимо потребовать,	чтобы уравнение
ψ(y1, y2 ) = 0	имело кратные корни, условием	которого	является равенство нулю	дискриминанта:

A12 − 4A2 A0 = 0 .

Согласно методу Г. Сеге принимается A2 = A1 = 0 и на основании этого составляется система дифференциальных уравнений для определения коэффициентов a11, a12 :

f		(	da11(y1)			,		a	(y	),		y	) = 0;
f		(				,		a	(y	),		y	) = 0;
	1		dy1					11	1			1
			dy1											(12.42)
			da		(y )									(12.42)
f		(	12		1		,	a	(y		),	y		) = 0.
f		(					,	a	(y		),	y		) = 0.
	2			dy				12	1			1
					1

Далее необходимо решить систему дифференциальных уравнений (12.42) относительно a11, a12 .

Найденные значения коэффициентов подставляются в выражение для функции Ляпунова и ее производной, после чего проверяется знакоопределенность функции V (y1, y2 ) и определяется знак производ-

ной dV / dt . На основании полученных результатов о знакоопределенности функции V (y1, y2 ) и знаке

dV / dt делается вывод об устойчивости системы автоматического управления по Ляпунову: система будет устойчивой, если получили, что V (y1, y2) > 0 , а dV / dt < 0 .

Метод Д. Шульца

Согласно этому методу функция Ляпунова записывается в виде

y	y1	y2
V = ∫ V T dy = ∫ V1(ξ1,0, K,0)dξ1 + ∫ V2 (y1,ξ2,0, K,0)dξ2 +
0	0	0	(12.43)
y2			(12.43)
y2
+ ∫	Vn (y1, y2 , K, yn−1,ξn )dξn ,
0

где V – градиент функции Ляпунова, т.е. который записывается в виде

a11y1 + a12 y2 +K+ a1n yn
a	21	y	+ a	22	y	2	+K+ a	2n	y	n
V =		1
. . . . . . . . .
a	n1	y	+ a	n2	y	2	+K+ a	nn	y	n
		1

V = {∂V / ∂y1, K,∂V / ∂yn} для системы уравнений n-го порядка,

(12.44)

Производная по времени от функции Ляпунова будет

dV = V T dy

(12.45)

где V T – транспонированный столбец V , т.е.

V T = (a y + a y

+K+ a

, K, a

y + a

+K+ a

11 1 12

n1 1

dy / dt = (dy1 / dt, dy2 / dt, K,dyn / dt).

В такой постановке задачи о выборе функции Ляпунова определению подлежат коэффициенты aij , при этом принимается условие, что aij = a ji = const . Для определения коэффициентов записывается усло-

вие выполнения неравенства dV / dt < 0 , из которого составляется система уравнений, разрешаемая относительно aij , i =1, n ; j =1, n . После определения коэффициентов записывается конкретное значение

функции Ляпунова и производится проверка условий V (y1, y2 , K, yn ) > 0 , по результатам которой делается вывод об устойчивости рассматриваемой системы автоматического управления.

Метод Лурье – Постникова

Согласно этому методу функция Ляпунова для системы квазилинейных уравнений, т.е. уравнений, содержащих линейную часть и аддитивно входящую нелинейность, записывается в виде:

y
V (y1, y2 , K, yn ) =V1(y1, y2 , K, yn ) + ∫ f (y)dy,	(12.46)
0

где V1(y1, y2 , K, yn ) – функция Ляпунова для линейной части, которая, как правило, пишется в виде квадратичной формы; f (y) – нелинейность, имеющая место в системе.

Анализ устойчивости сводится к конкретной записи функции Ляпунова и ее производной с последующей проверкой их знаков и применением теоремы об устойчивости.

Функция Ляпунова в виде (12.46) уже была использована в разделе 12.3.4 при рассмотрении общей методики применения теоремы Ляпунова.

12.3.6 ПРИМЕРЫ ПОСТРОЕНИЯ ФУНКЦИЙ ЛЯПУНОВА

Пример 12.2 Пусть нелинейная система автоматического управления описывается нелинейным дифференциальным уравнением второго порядка

d 2 y(t)	+	dy(t)	+ y3	(t) = 0.
dt 2		dt

Исследовать эту систему на устойчивость вторым методом Ляпунова, используя при построении функции Ляпунова метод Г. Сеге.

Исходное нелинейное дифференциальное уравнение второго порядка следует привести к системе дифференциальных уравнений первого порядка

dy1(t)dtdy1(t)dt

=y2 (t);

=−y13(t) − y2 (t).

Согласно методу Г. Сеге функция Ляпунова имеет вид

					V = a (y )y2 + 2a (y )y + y2.
									11			1	1					12			1		1			2
Производная отнее сучетом системы дифференциальных уравнений
dV =			da11(y1)		y2 y		2		+ 2a (y )y y											2	+ 2	da12 (y1)						y y2		+
dV =					y2 y				+ 2a (y )y y												+ 2							y y2		+
dt			dy1	1								11	1		1									dy1			1		2
dt			dy1																					dy1
		+ 2a (y )y				2	− 2a (y )y y										2			− 2a (y )y4								− 2y2		− 2y3 y			.
		12		1		2				12			1	1			2				12			1		1			2		1	2
Образуем функцию ψ(y) = A2 y22 + A1y2 + A0										из производной dV / dt																			по степеням y2 , сравнивая выраже-
ния dV / dt и ψ(y) , получим
					A	= 2				da12 (y1)					y				+ a (y					) −1			;
					A	= 2									y				+ a (y					) −1			;
				2								dy				1					12		1
													1
A =	da11(y1)			y + 2a (y ) y −2														da12 (y1)							y + a (y ) y −2y3 ;
A =				y + 2a (y ) y −2																					y + a (y ) y −2y3 ;
1			dy	1					11 1				1								dy					1	12 1				1		1
		1																			1
				A = −2							da12 (y1)					y + a (y ) y4.
				A = −2												y + a (y ) y4.
				0								dy						1			12			1		1
													1
Для получения устойчивости во всей области (y1, y2 ) необходимо,																															чтобы коэффициенты A1 = A2 = 0 ,
что приводит к системе дифференциальных уравнений относительно a11(y1)																																и a12 (y1) :
				da11(y1) y									+ 2a				(y				) = 2(1+ y2 );
						dy1						1			11					1						1
						dy1
				da				(y )
						11			1			y1	+ a12 (y1)								=1.
						dy						y1	+ a12 (y1)								=1.
									1
Решение первого уравнения, т.е. a11(y1) ищется в виде
										a (y ) = αy2											+β.
												11	1							1
Подставив это решение в уравнение, получим
					2αy2 + 2αy2									+ 2β = 2 + 2y2.
									1				1											1
Приравняв коэффициенты			при	одинаковых										степенях												y1 ,		определим значения коэффициентов
α =1/2 , β =1.
Решением второго уравнения является a12 (y1) = γ ,																	γ =1 .
Подставим найденные значения a11 и a12										в функцию Ляпунова и ее производную
			V = 1 y4					+ y2				+ 2y y				+ y					2 ,		dV			= −2y4			,
				2		1				1			1		2						2		dt				1

видно, что dV / dt < 0 при любых значениях y1 . А это и указывает на устойчивость рассматриваемой сис-

темы автоматического управления по Ляпунову.

Пример 12.3 Исследовать устойчивость нелинейной системы, динамика которой описывается

системой уравнений

dy1(t)dtdy2 (t)dt

=−3y2 − F(y1)y1;

=−2y2 + F(y1)y1,

используя второй метод Ляпунова и форму Д. Шульца при построении функции Ляпунова.

В соответствии с методом Д. Шульца градиент функции Ляпунова представляется в виде

V = α11y1 + α12 y2 .α21y1 + α22 y2

Производная от функции Ляпунова dVdt = V T dVdt , или в соответствии с исходной системой

dVdt = −y12[α11F(y1) − α21F(y1)]+ y1y2 ×

×[−3α11 − α12F(y1) − 2α21 + α22F(y1)]− y22[2α22 + 3α12 ].

Положим α12 = α21 = 0 , тогда

dVdt = −α11F(y1)y12 − 2α22 y22 + y1y2[−3α11 + α22F(y1)].

Если −3α11 −α21F(y1) = 0, то dV / dt < 0 . Это возможно, если α11 = α322 F(y1) .

В соответствии с последним выражением градиент функции Ляпунова и ее производная запишутся в виде

	α	22							2	2
V =		22	F(y	)y	,	dV		α22F		(y1)y1	2
			F(y	)y		dV		α22F		(y1)y1	2
	3		1	1		dt	= −		3		−2α22 y2 .
						dt			3
α22 y2

Согласно формуле (12.43) получим функцию Ляпунова

V = y1	α22	F(ξ)ξdξ + y2	α22ηdη.
V = y1	3	F(ξ)ξdξ + y2	α22ηdη.
∫	3	∫
0		0
y1
Приняв α22 = 6 , запишем V = 2∫F(ξ)ξdξ+3y22 .
0

Если произведение F(y1)y1 = X находится в первом и третьем квадрантах, то функция Ляпунова по-

ложительно определенна, а ее производная отрицательно определенна, т.е. V > 0 , dV / dt < 0 , но это и указывает на устойчивость рассматриваемой системы.

Пример 12.4 Найти условие устойчивости нелинейной системы автоматического регулирования, описываемой системой уравнений

dy1(t)dtdy2 (t)dt

+ay1 = bF(y2 );

=cy1 −βF(y2 ),

с помощью второго метода Ляпунова.

Функция Ляпунова записывается в соответствии с методом Лурье – Постникова в виде

V = αy12 + ∫F(ξ)dξ, α > 0,

производная от этой функции dVdt = −2αay12 + 2dF(y2 )y1 −βF 2 (y2 ),

где d = αb +1/ 2c .

Условие отрицательной определенности dV / dt записывается в виде β > 0 , (db + c / 2)2 − 2αaβ < 0 . Для

того, чтобы последнее неравенство имело положительное решение α > 0 , необходимо и достаточно выполнение неравенства aβ > bc , которое обеспечивает положительность обоих корней уравнения

α2b2 + α(bc − 2αβ) + c2 / 4 = 0.

Таким образом, если aβ > bc , то рассматриваемая система автоматического регулирования устойчи-

ва.

12.4 Критерий абсолютной устойчивости Попова

Большие возможности для исследования устойчивости и даже качества нелинейных систем открыва-
ет предложенный в 1960 году румынским ученым Пóповым критерий абсолютной устойчивости,
особенно его геометрическая трактовка, позволяющая привлечь к исследованию рассматриваемого
класса нелинейных систем частотные методы.
Рассматривается нелинейная система, на которую действует конечного вида произвольное воздей-
ствие f (t) , ограниченное лишь тем, что оно считается исчезающим, т.е. lim f (t) = 0 (рис. 12.7).
						t →∞
Пусть линейная часть системы описывается передаточной функцией W (s) , а во временной области –
весовой функцией w(t) , нелинейный элемент характеризуется статической характеристикой y(t) = Φ[x(t)].
		f(t)		x	НЭ	y

			- z(t)		W(s)

	Рис. 12.7 Нелинейная система с исчезающим воздействием
Вся нелинейная система в интегральной форме описывается уравнением
		t
x(t) = f (t) − z(t) = f (t) − ∫w(t − τ)Φ[x(τ)]dτ,					(12.47)
		0
изображение по Лапласу которого x(s) = f (s) −W (s)L{Φ[x(t)]}.
Состояние равновесия x = 0		будет устойчивым по Ляпунову, если для любого сколь угодно малого
положительного ε существует другое положительное η(ε)						такое, что при sup f (t) = η0 , η0 < η имеет ме-
сто неравенство x(t) ≤ ε . Если η неограниченно, имеет место устойчивость в целом.
Абсолютной	устойчивостью равновесия называется устойчивость в целом,						имеющая место для
всех характеристик Φ(x) , принадлежащих к определенному классу.
Будем рассматривать устойчивость для характеристик Φ(x) , лежащих в углу α,							т.е. принадлежащих
подклассу (0, k) (рис. 12.8).
Если равновесие абсолютно устойчиво, то оно абсолютно устойчиво и для всех прямолинейных ха-
рактеристик y = hx , где 0 ≤ h ≤ k,		поскольку эти прямые относятся к данному подклассу.
Исходная нелинейная система (рис. 12.7) представляет собой по своей структуре замкнутую систе-
				му, в которой нелинейный элемент охвачен отрицательной
	y	y = k x		обратной связью с линейным звеном W (s) . Если провести ли-
		α = arctgk		неаризацию нелинейной характеристики Φ(x(t)) , то получен-
				ную уже замкнутую линейную систему можно исследоватьна
				устойчивостьспомощьючастотногокритерияНайквиста.
	0	x		Рассмотрим основной случай, когда линейная часть
				системы устойчива, т.е. ее характеристическое уравнение
				не имеет правых корней или тоже самое, что W (s) не имеет
				правых полюсов и тогда годограф вектора разомкнутой
Рис. 12.8 Класс нелинейных				системы линеаризованной характеристики hW (iω) не пере-
				секает отрезка (−∞, −1) действительной оси. В соответствии
характеристик				с критерием Найквиста этого условия достаточно, чтобы
замкнутая линейная система была устойчива. Так как 0 ≤ h ≤ k , то достаточным условием устойчивости
всех линейных систем из подкласса (0, k)			будет условие,			чтобы W (iω) не пересекала отрезка действи-
тельной оси (−∞, −1/ k) .
Можно показать, что это условие необходимо и достаточно. Действительно, пусть линейная часть
устойчива, но W (iω) пересекает четное число раз отрезок (−∞, −1/ k) . Изменяя h в пределах от 0 до k ,
тем самым перемещается правая граница критического отрезка, причем значению h = 0 соответствует
точка −∞ , а h = k	– −1/ k . Всегда можно выбрать h				внутри заданных границ так, чтобы правая граница
критического отрезка попала в любую точку отрезка (−∞, −1/ k) .

W (iω)

Если характеристика W (iω) пересекает четное число раз отрезок (−∞, −1/ k) , то выберется значение h

так, чтобы число пересечений стало на единицу меньше, но тогда замкнутая система становится неустойчивой. Таким образом, чтобы замкнутая система оставалась устойчивой при любых h , заключенных в пределах 0 ≤ h ≤ k , необходимо и достаточно, чтобы нигде не пересекала отрезок (−∞, −1/ k) оси

абсцисс.

Для произвольной нелинейной функции из подкласса (0,k) достаточное условие абсолютной устой-

чивости было сформулировано Поповым и выглядит следующим образом.

Для того, чтобы положение равновесия нелинейной системы с устойчивой линейной частью было устойчиво, достаточно выполнение следующих условий:

1 Существует такое действительное число α , при котором действительная часть функции Попова П(iω) была положительна

Re П(iω)= Re[(1+ iαω)W (iω)+1/ k]> 0.

(12.48)

2 Функция Φ(x) принадлежит подклассу (0,k) , т.е. 0 ≤ Φ(x) / x ≤ k .

Доказательство этой теоремы не приводится, но рассматривается геометрическая трактовка. Для этого вводятся следующие характеристики видоизмененной частотной характеристики линейной части W *(iω), связанной с исходной W (iω) соотношениями:

	ReW *(iω)= ReW (iω);	(12.49)
	ImW *(iω)= ωImW (iω),	(12.49)
	ImW *(iω)= ωImW (iω),

т.е. действительная часть видоизмененной характеристики равна действительной части исходной, а мнимая равна мнимой части исходной, умноженной на ω. Так как ImW (iω)= 0 и ImW *(iω)= 0 одновременно, то точки пересечения действительных характеристик совпадают. Действительная и мнимая части видоизмененной характеристики W *(iω) являются четными функциями ω. Если степень числителя W (iω) не выше степени знаменателя и W (iω) имеет не более одного полюса в начале координат, то при ω→ ∞ ReW *(iω) и ImW *(iω) стремятся к конечным пределам и характеристика W *(iω) лежит в конечной

части плоскости целиком. Пусть

W (iω) = U (ω) + iV (ω);

W *(iω) = U *(ω) + jV *(ω),

тогда

Re[(1+iαω)W (iω) +1/ k]=U (ω) −αωV (ω) +1/ k > 0 (12.50)

или

U *(ω) −αV *(ω) +1/ k > 0.

Критическим случаем является случай, когда

U *(ω) −αV *(ω) +1/ k = 0,

который дает в координатах U *, V * уравнение прямой линии, касающейся характеристики W *(iω). Прямая проходит через точку (−1/ k, iω) и имеет угловой коэффициент 1/ α .

Когда U *(ω) −αV *(ω) +1/ k > 0 , W *(iω) лежит в части плоскости, включающей начало координат, т.е.

правее прямой.

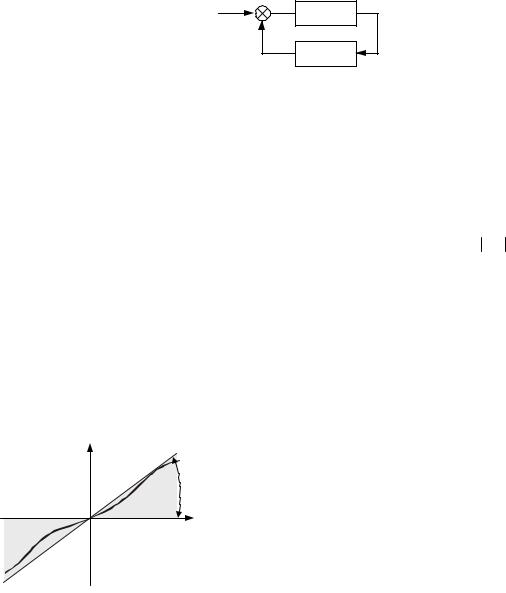
Таким образом, для абсолютной устойчивости равновесия достаточно, чтобы на плоскости видоизмененной частотной характеристики W *(iω) линейной части системы можно было провести прямую че-

рез точку (−1/ k, i0) так, чтобы W *(iω) целиком располагалась справа от этой прямой (рис. 12.9, а).

На рис. 12.9, б приведен случай, когда отделяющую прямую построить нельзя и судить об устойчивости также нельзя.

Критерий Попова распространен также на системы с неустойчивой или нейтральной линейной частью. В этом случае должны выполняться условия

Re(1+ iαω)W1(iω) +1/ k > 0; r < Φ(x)/ x < k + r, (12.53)

V*	а)
-1
k
	U*

V*	б)
1	U*
- k

Рис. 12.9 Геометрическая трактовка абсолютной устойчивости системы:
			а – устойчивая систем; б – неустойчивая
т.е. нелинейная характеристика должна укладываться в углу, ограниченном прямыми с угловыми коэф-
фициентами r	и k + r . При этом r выбирается так, чтобы 1+ rW (iω) имела все нули в левой полуплоско-
сти, а W1(iω) – видоизмененная характеристика линейной части
				W (iω) = W (iω) .
				1	1+ rW (iω)
					1+ rW (iω)
Между критерием абсолютной устойчивости Попова и вторым методом Ляпунова существует глу-
бокая связь. Было доказано, что если выполняется условие абсолютной устойчивости Попова, то суще-
ствует типовая функция Ляпунова –				квадратичная форма плюс нелинейность, причем условие
Re(П(iω)) > 0 является необходимым и достаточным.
Пример 12.5 Нелинейная система второго порядка имеет линейную часть, описываемую уравне-
нием
						1
				W (s) = s2 + 2hω0s + ω02 .
Требуется определить, при каких значениях k					система будет абсолютно устойчива, если характери-
стика нелинейного элемента лежит в секторе (0,k ).
Видоизмененная характеристика линейной части будет
		*		ω2 −ω2			2hω	ω2
		*		0			0
	W		(iω) = (ω02 − ω2 )2 + 4h2ω02ω2 − (ω02 − ω2 )2 + 4h2ω02ω2 .
Анализ этой характеристики показывает, что при всех ω мнимая часть характеристики отрицатель-
	i V*			на, а это говорит о том, что вся характеристика W *(iω) лежит в
	i V*			нижней полуплоскости (рис. 12.10).
				При частотах ω = 0 ,				ω =1, ω= ∞ она имеет общие точки с
				характеристикой W (iω) .
1				Касательная к кривой АФХ W *(iω) в начале координат
1				проходит под углом arctg(2hω0 ) к вещественной оси. Сама кри-
- k	arctg 2 h ω0
			U*	вая W *(iω)		лежит правее этой касательной, поэтому всегда
				можно провести прямую Попова через точку −1/ k под неко-
				торым углом α (рис. 12.10). Система абсолютно устойчива
				при всех	k	и для всех однозначных нелинейных характери-
Рис. 12.10 Видоизмененная				стик, принадлежащих сектору(0, ∞).
	АФХ					12.5 Тренировочные задания
						12.5 Тренировочные задания

1В нелинейных системах исследуется устойчивость движения. Различают возмущенное движение

иневозмущенное движение. Основными видами устойчивости движения являются понятия устойчиво-

сти движения по Ляпунову и асимптотической устойчивости. Кроме того для нелинейных систем существуют такие понятия, как устойчивость в "малом" и устойчивость в "большом".

Для исследования устойчивости в "малом" используется первый метод Ляпунова, который позволяет судить об устойчивости нелинейной системы по линейной системе первого приближения.

А Какое движение называется возмущенным движением и какое движение называется невозмущенным движением?

В Какой смысл имеет понятие устойчивости движения системы по Ляпунову и чем оно отличается от асимптотической устойчивости?

С Какие теоремы были доказаны Ляпуновым в первом методе исследования устойчивости в "малом" состояния равновесия нелинейной системы.

2 Как известно, достаточные условия устойчивости нелинейных систем дает второй метод Ляпунова, позволяющий исследовать устойчивость в "большом". Согласно этому методу в рассмотрение вводится функция V (y1, y2, ..., yn ) , заданная в фазовом пространстве и обладающая следующими свойствами: не-

прерывна со всеми своими частными производными в некоторой открытой области, содержащей начало координат; при y1 = y2 =... = yn = 0 – V (y1, y2 , ..., yn ) = 0; внутри рассматриваемой области V является знако-

определенной функцией, т.е. V > 0 или V < 0 .

А. М. Ляпуновым были сформулированы три теоремы: об устойчивости, об асимптотической устойчивости и о неустойчивости. Так для доказательства асимптотической устойчивости строится и исследуется производная по времени функции Ляпунова, которая в силу системы дифференциальных уравнений, описывающих нелинейную систему, должна быть знакоопределенной функцией противоположного с V знака.

Если найти такую функцию V удастся, то устойчивость нелинейной системы будет доказана, причем устойчивость в "большом". Единого подхода к построению функции V (y1, y2, ..., yn ) не существует,

но имеются рекомендации по составлению этой функции для исследования определенного класса систем.

А Какая теорема физики лежит в основе второго метода Ляпунова?

В Какими свойствами должна обладать функция Ляпунова и ее производная по времени, чтобы нелинейная система была устойчива ?

С Как Вы объясните, что второй метод Ляпунова дает устойчивость нелинейной системы в "большом"?

3 Для исследования устойчивости определенного класса нелинейных систем применяют критерий абсолютной устойчивости. Этот критерий относится к группе частотных критериев устойчивости. Рассматриваемая нелинейная система представляет собой замкнутую систему и состоит из линейной части, характеризуемой амплитудно-фазовой характеристикой W (iω), и нелинейного элемента со статической

характеристикой Φ(x) из подкласса (0,k) , т.е. 0 ≤ Φ(x) / x ≤ k , стоящего в отрицательной обратной связи.

Для устойчивости состояния равновесия нелинейной системы с устойчивой линейной частью достаточно выполнения условия, что действительная часть функций Попова Π(iω) положительна.

А Как Вы понимаете абсолютную устойчивость?

В Что представляет собой видоизмененная амплитудно-фазовая характеристика линейной части, и как последняя связана с исходной?

СДайте геометрическую трактовку критерия абсолютной устойчивости.

12.6Тест

1 Для асимптотической устойчивости необходимо, чтобы при t → ∞

А || y(t) − y* (t) ||< ε. В || y(t) − y* (t) ||> ε. С || y(t) − y*(t) ||→ 0.

2 Если нелинейная система второго порядка описывается системой дифференциальных уравнений первого порядка

dydt1 = P(y1, y2).dy2 = Q(y1, y2),dt

то состояние равновесия определяется решением следующей системы

АP(y1, y2) = 0;Q(y1, y2) = 0.

ВP(y1, y2 ) = const;Q(y1, y2 ) = const.

СP(y1, y2) = ∞;

Q(y1, y2) = ∞.

3 Линеаризованное уравнение первого приближения записывается в виде

А An y(n) (t) + ... + A1y′(t) + A0 y(t) = 0. В An y(n) (t) +... + A1y′(t) + A0 y2 (t) = 0.

С An (y(n) (t))2 +...+ A1(y′(t))2 + A0 y2 (t) = 0.

4 Знакоопределенной функцией является функция вида

А V = y1 + y2 +...+ yn.

В V = y12 + y22 +...+ yn2.

С V = (y12 + y22 ) + (y22 + y32 ) ...+ y42.

5 Функция Ляпунова при y1 = y2 =... = yn = 0 принимает значение

А V (y1, y2, ..., yn )= ∞.

BV (y1, y2, ..., yn )= 0.

CV (y1, y2, ..., yn )= const.

6 В фазовом пространстве функция Ляпунова представляет собой

А Плоскость.

В Многогранник. С Параболоид.

7 Производная от функции Ляпунова по времени в силу системы дифференциальных уравнений, описывающих нелинейную систему

dydti = Fi (yi , y2, ..., yn ), i = in,

записывается в виде

∂V

F +

∂V

F +... +

∂V

F .

∂y

∂V

F ...

∂V

F + F F ... F .

∂y

1 2

∂V

+...

∂V

F .

∂y

n−1

8 Критерий абсолютной устойчивости Попова используется для исследования устойчивости нелинейных систем со статическими характеристиками вида

9 Состояние равновесия нелинейной системы будет устойчиво, если на плоскости видоизмененной АФХ W *(iω) линейной части, если W *(iω) и прямая, проведенная через точку (−1/ K, iω) , расположены следующим образом

iV*

А	u*
1	u*
– –
k

iV*

B	u*
1	u*
– –
k

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 2223 / 2623 24 25 26 > Следующая >>>

Соседние файлы в папке ЛЕКЦИЯ_1

#
08.02.20162.6 Mб50Лекция_1_Н.pdf
#
08.02.20162.64 Mб67Основы теории автоматического управления - УП - Лазарева-Мартемьянов - 2004 - 352.pdf
#
08.02.2016960.51 Кб88ТАУ01-Введение в теорию управления.doc
#
08.02.20162.36 Mб22ТАУ_ТЕМА1 ВВЕДЕНИЕ В ТЕОРИЮ УПРАВЛЕНИЯ.pptx